目录
- 0 专栏介绍
- 1 时序差分强化学习
- 2 策略评估原理
- 3 策略改进原理
- 3.1 SARSA算法
- 3.2 Q-Learning算法
0 专栏介绍
本专栏重点介绍强化学习技术的数学原理,并且采用Pytorch框架对常见的强化学习算法、案例进行实现,帮助读者理解并快速上手开发。同时,辅以各种机器学习、数据处理技术,扩充人工智能的底层知识。
🚀详情:《Pytorch深度强化学习》
1 时序差分强化学习

在Pytorch深度强化学习1-5:详解蒙特卡洛强化学习原理中我们指出,在现实的强化学习任务中,转移概率、奖赏函数甚至环境中存在哪些状态往往很难得知,因此有模型强化学习在实际应用中不可行,而需要免模型学习技术,即假设转移概率和环境状态未知,奖赏也仅是根据经验或需求设计。蒙特卡洛强化学习正是免模型学习中的一种,其核心思想是使用蒙特卡洛方法来估计各个状态-动作对的值函数。通过对大量的样本进行采样,并根据它们的累积奖励来评估状态-动作对的价值,智能体可以逐步学习到最优策略。
本节介绍的时序差分强化学习(Temporal Difference Reinforcement Learning)则是另一类免模型学习算法,它结合了动态规划和蒙特卡洛强化学习的优点,用于在未知环境中进行决策。
2 策略评估原理
策略评估本质上是求解状态值函数 V π ( s ) V^{\pi}\left( s \right) Vπ(s)或状态-动作值函数 Q π ( s , a ) Q^{\pi}\left( s,a \right) Qπ(s,a),数值越大表明策略回报越高。从定义出发,蒙特卡洛强化学习核心是采样近似,基于采样的算法通常采用增量更新方式节省内存
Q π ( s , a ) = E [ R t ] ∣ s t = s , a t = a ≈ 1 n ∑ i = 1 n R t , i = n 次增量 Q π ( s , a ) × c o u n t ( s , a ) + R t c o u n t ( s , a ) + 1 = n 次增量 Q π ( s , a ) + 1 c o u n t ( s , a ) + 1 ( R t − Q π ( s , a ) ) \begin{aligned}Q^{\pi}\left( s,a \right) &=\mathbb{E} \left[ R_t \right] \mid_{s_t=s,a_t=a}^{}\\&\approx \frac{1}{n}\sum_{i=1}^n{R_{t,i}}\\&\xlongequal{n\text{次增量}}\frac{Q^{\pi}\left( s,a \right) \times \mathrm{count}\left( s,a \right) +R_t}{\mathrm{count}\left( s,a \right) +1}\\&\xlongequal{n\text{次增量}}Q^{\pi}\left( s,a \right) +\frac{1}{\mathrm{count}\left( s,a \right) +1}\left( R_t-Q^{\pi}\left( s,a \right) \right)\end{aligned} Qπ(s,a)=E[Rt]∣st=s,at=a≈n1i=1∑nRt,in次增量count(s,a)+1Qπ(s,a)×count(s,a)+Rtn次增量Qπ(s,a)+count(s,a)+11(Rt−Qπ(s,a))
因为采样过程通常以万次计,因此可以用一个较小的正数 α \alpha α来描述,超参数 α \alpha α可理解为模型的学习率, R t − Q π ( s , a ) R_t-Q^{\pi}\left( s,a \right) Rt−Qπ(s,a)称为蒙特卡洛误差
Q π ( s , a ) = n 次增量 Q π ( s , a ) + α ( R t − Q π ( s , a ) ) Q^{\pi}\left( s,a \right) \xlongequal{n\text{次增量}}Q^{\pi}\left( s,a \right) +\alpha \left( R_t-Q^{\pi}\left( s,a \right) \right) Qπ(s,a)n次增量Qπ(s,a)+α(Rt−Qπ(s,a))
动态规划强化学习核心是自我迭代
Q π ( s , a ) = E [ R t ] ∣ s t = s , a t = a = ∑ s ′ ∈ S P s → s ′ a [ R s → s ′ a + γ ∑ a ′ ∈ A π ( s ′ , a ′ ) Q π ( s ′ , a ′ ) ] Q^{\pi}\left( s,a \right) =\mathbb{E} \left[ R_t \right] \mid_{s_t=s,a_t=a}^{}=\sum_{s'\in S}{P_{s\rightarrow s'}^{a}}\left[ R_{s\rightarrow s'}^{a}+\gamma \sum_{a'\in A}{\pi \left( s',a' \right) Q^{\pi}\left( s',a' \right)} \right] Qπ(s,a)=E[Rt]∣st=s,at=a=s′∈S∑Ps→s′a[Rs→s′a+γa′∈A∑π(s′,a′)Qπ(s′,a′)]
根据动态特性和当前 Q π ( s , a ) Q^{\pi}\left( s,a \right) Qπ(s,a),具体计算出下一次迭代的 Q π ( s , a ) Q^{\pi}\left( s,a \right) Qπ(s,a)
动态规划强化学习的优点是计算准确且效率高,但无法适应无模型场景;蒙特卡洛强化学习的优点是克服无模型障碍,但有更新延迟现象。时序差分强化学习是动态规划与蒙特卡洛的折中
Q π ( s t , a t ) = n 次增量 Q π ( s t , a t ) + α ( R t − Q π ( s t , a t ) ) = n 次增量 Q π ( s t , a t ) + α ( r t + 1 + γ R t + 1 − Q π ( s t , a t ) ) = n 次增量 Q π ( s t , a t ) + α ( r t + 1 + γ Q π ( s t + 1 , a t + 1 ) − Q π ( s t , a t ) ) ⏟ 采样 \begin{aligned}Q^{\pi}\left( s_t,a_t \right) &\xlongequal{n\text{次增量}}Q^{\pi}\left( s_t,a_t \right) +\alpha \left( R_t-Q^{\pi}\left( s_t,a_t \right) \right) \\\,\, &\xlongequal{n\text{次增量}}Q^{\pi}\left( s_t,a_t \right) +\alpha \left( r_{t+1}+\gamma R_{t+1}-Q^{\pi}\left( s_t,a_t \right) \right) \\\,\, &\xlongequal{n\text{次增量}}{ \underset{\text{采样}}{\underbrace{Q^{\pi}\left( s_t,a_t \right) +\alpha \left( r_{t+1}+{ \gamma Q^{\pi}\left( s_{t+1},a_{t+1} \right) }-Q^{\pi}\left( s_t,a_t \right) \right) }}}\end{aligned} Qπ(st,at)n次增量Qπ(st,at)+α(Rt−Qπ(st,at))n次增量Qπ(st,at)+α(rt+1+γRt+1−Qπ(st,at))n次增量采样 Qπ(st,at)+α(rt+1+γQπ(st+1,at+1)−Qπ(st,at))
其中 r t + 1 + γ Q π ( s t + 1 , a t + 1 ) − Q π ( s t , a t ) r_{t+1}+\gamma Q^{\pi}\left( s_{t+1},a_{t+1} \right) -Q^{\pi}\left( s_t,a_t \right) rt+1+γQπ(st+1,at+1)−Qπ(st,at)称为时序差分误差。当时序差分法只使用一步实际奖赏时称为 T D ( 0 ) TD(0) TD(0)算法,扩展为 T D ( n ) TD(n) TD(n)算法,当 n n n充分大时退化为蒙特卡洛强化学习
3 策略改进原理
类似地,时序差分强化学习同样分为同轨策略和离轨策略,前者的代表性算法是SARSA算法,后者的代表性算法是Q-learning算法
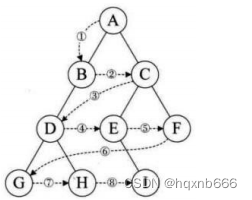
3.1 SARSA算法
SARSA算法流程图如下所示

3.2 Q-Learning算法
Q-Learning算法流程图如下所示

🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …