基于大语言模型的复杂任务认知推理算法CogTree

近日，阿里云人工智能平台PAI与华东师范大学张伟教授团队合作在自然语言处理顶级会议EMNLP2023上发表了基于认知理论所衍生的CogTree认知树生成式语言模型。通过两个系统：直觉系统和反思系统来模仿人类产生认知的过程。直觉系统负责产生原始问题的多个分解假设，反思系统对直觉系统产生的假设进行验证，并选择更有可能的假设进行后续生成，直到达到最终结果。通过上述双系统的迭代式生成，可以提升大模型的解题准确度。

论文：

Junbing Yan, Chengyu Wang, Taolin Zhang, Xiaofeng He, Jun Huang, Wei Zhang. From Complex to Simple: Unraveling the Cognitive Tree for Reasoning with Small Language Models. EMNLP 2023 (Findings)

背景

随着深度学习在自然语言处理、机器翻译等任务上的不断发展，人们对如何将深度学习应用到自然语言处理中越来越感兴趣，由此出现了大语言模型（例如GPT-3.5），并已在文本生成、情感分析、对话系统等多个任务上取得了重大突破。大语言模型通常基于大规模文本数据进行预训练，然后通过微调在特定任务上进行优化，以生成高质量的文本输出。然而，对于语言模型而言，复杂的逻辑推理问题和数学问题的求解仍然是很困难的。并且，传统的语言模型缺乏认知能力。在处理涉及冗长的推理链或多步解决方案的问题时，对于问题及其当前回答的评估是很重要的。然而，目前的方法例如Chain-of-thought等通常缺乏对于中间过程的验证。并且大型语言模型的部署和推理成本相对较高，特别是在利用无参数更新的推理增强技术时。这些技术需要大量的上下文和多步的答案生成，进一步增加了推理成本和时间。

因此，本文研究面向轻量化大模型的复杂任务推理，使用较小规模的模型（7B），构建双系统生成推理树，大大增强模型在复杂数学问题和逻辑推理问题上的回答能力。提出了一种大模型面向复杂数学问题的求解方法。该方法基于人类的认知理论，通过两个系统：直觉系统和反思系统来模仿人类产生认知的过程。直觉系统负责产生原始问题的多个分解假设，反思系统对直觉系统产生的假设进行验证，并选择更有可能的假设进行后续生成，直到达到最终结果。通过上述双系统的迭代式生成，可以提升大模型的解题准确度。

算法概述

为了解决上述大模型对复杂任务推理准确度不高且推理成本大的问题，CogTree采用双系统的方式，用大模型分别构建两个系统：直觉系统和反思系统，使用直觉系统生成原问题分解的假设，使用反思系统验证假设的正确性，引导直觉系统后续的生成。模型框架图如下所示：

通过双系统迭代式的生成一棵推理树，增强大模型的推理能力。本方法的创新性是面向大语言模型，设计了一套新的推理框架，增强大模型在复杂数学问题上的推理能力。

直觉系统

直觉系统的生成能力是构建认知树的基础。因此，选择仅包decoder-only的模型（例如，GPT2-XL或LLaMA-7B）作为直觉系统。通过上下文方法来增强直觉系统的能力。定义查询 $Q$ 为逻辑推理问题的最终目标或数学问题。在逻辑推理问题的情况下，分解 $D$ 涉及将目标进一步分解为较小问题，通过对这些分解进行推理，可以实现最终目标。对于数学问题，它指的是从原始问题中导出的子问题之一，解决这个子问题有助于解决整个原始问题。分解集合表示训练集中所有示例的分解集合。从推理分解集合中检索k个示例（例如，查询： $Q$ ；分解：询： $D$ ），然后将它们用作模型输入的上下文。输出可以生成为y∼fθ(y∣x,z1…k)。这里， $z$ 代表从分解集合 $Z$ 中检索到的k个示例，其中 $Z=\{z_1,\cdots, z_L\}$ 。使用直觉系统获取当前查询的表示，并计算与集合中其他查询的表示的余弦相似度。然后，我们从集合中检索出最相似的k个查询。其中 $[y] \sim f_\theta(y | x, z_{1 \cdots K})$ 是一个连续语言序列。

反思系统

反思系统在作用上与直觉系统不同。直觉系统依赖于快速直觉进行生成，而反思系统的作用是评估直觉系统的生成结果以确定其可接受性。反思系统通过采用两种方法来验证结果：中间过程的验证和整个推理链的验证。给定当前状态 $s$ （查询： $Q$ 与分解： $D$ ），使用与直觉系统相同的模型架构的反思系统来生成一个验证当前状态的分数 $v$ 。这可以表示为 $V(f_\theta,s) \sim f_\theta(v | s)$ 。此外，基于完整的推理链 $S=\{s_1,\cdots, s_i,\cdots, s_n\}$ 。使用反思系统来产生一个整体分数 $o$ ，可以表示为 $O(f_\theta,S) \sim f_\theta(o | S)$ 。反思系统与直觉系统不同，其主要任务是评估和验证当前状态和整个推理链的可行性，而不是像直觉系统那样产生快速假设。这种评估过程有助于确保生成的假设和推理过程是合理的。

训练

直觉系统

Supervised Fine-tuning (SFT)已经证明了其在对其人类意图上的有效性。在我们的方法中，直觉系统通过利用上下文示例将查询 $Q$ （即复杂问题）分解为子问题。由于我们使用生成模型作为直觉系统，因此在自回归计算期间，仅对生成的文本（不包括给定的上下文）进行损失计算。给定一个长度为 $N$ 的样本，表示为 $X$ ，其中 $X=\{x_1,\cdots, x_i,\cdots, x_n\}$

。我们定义上下文示例的序列长度为 $M$ 。我们使用标准的语言建模目标来最大化以下似然函数： $\mathcal{L}_{\mathcal{IS}}=\sum_{i>M}^N log \ P(x_i | x_1, \cdots, x_{i-1}; \theta)$ 。

反思系统

反思系统采取与直觉系统相同的训练方法，利用正负样本让模型从中生成分类结果。由于反思系统主要关注状态 $s$ 的判断，损失函数可以定义如下： $\mathcal{L}_{\mathcal{RS}} = \log P(v | s; \theta)$ 。

算法精度评测

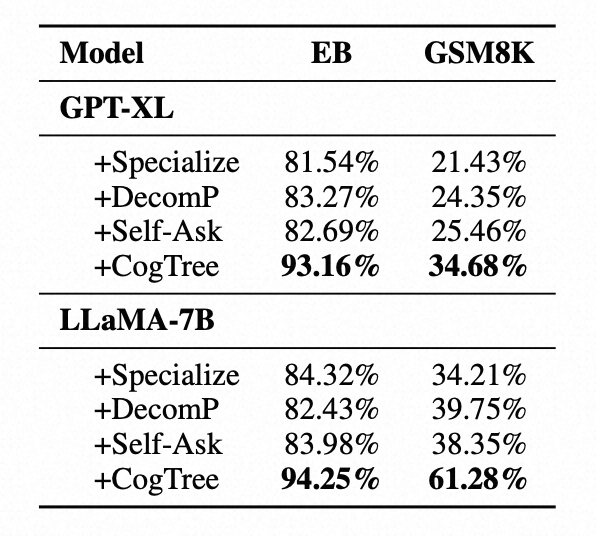
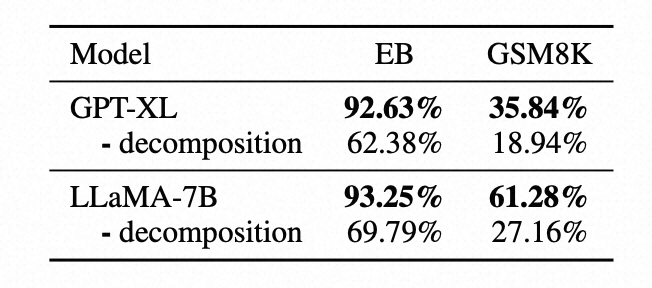
为了验证CogTree算法的有效性，我们在Entailment Bank逻辑推理数据集以及GSM8K数学问题数据集上进行了测试，效果证明CogTree对大模型复杂任务上的回答准确率提升明显：

我们也将算法与其他基于大模型微调的方法进行对比，证明了CogTree框架的有效性。

为了更好地服务开源社区，CogTree算法的源代码即将贡献在自然语言处理算法框架EasyNLP中，欢迎NLP从业人员和研究者使用。

EasyNLP开源框架：GitHub - alibaba/EasyNLP: EasyNLP: A Comprehensive and Easy-to-use NLP Toolkit

参考文献

Chengyu Wang, Minghui Qiu, Taolin Zhang, Tingting Liu, Lei Li, Jianing Wang, Ming Wang, Jun Huang, Wei Lin. EasyNLP: A Comprehensive and Easy-to-use Toolkit for Natural Language Processing. EMNLP 2022
Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. 2021a. Training verifiers to solve math word problems. CoRR, abs/2110.14168
Denny Zhou, Nathanael Schärli, Le Hou, Jason Wei, Nathan Scales, Xuezhi Wang, Dale Schuurmans, Olivier Bousquet, Quoc Le, and Ed H. Chi. 2022. Least-to-most prompting enables complex reasoning in large language models. CoRR, abs/2205.10625
Jonathan St B. T. Evans. 1984. Heuristic and analytic processes in reasoning. British Journal of Psychology, 75(4):451–468

论文信息

论文标题：From Complex to Simple: Unraveling the Cognitive Tree for Reasoning with Small Language Models
论文作者：严俊冰、汪诚愚、张涛林、何晓丰、黄俊、张伟
论文pdf链接：https://arxiv.org/abs/2311.06754

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/215351.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！