UG NX二次开发(C++)-库缺少需要的入口点的原因与解决方案

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

  • 1、前言
  • 2、“库缺少需要的入口点”错误展示
  • 3、可能出现的原因与解决方案
    • 3.1 对于采用CTRL+U方式调用
    • 3.2 对于menu菜单下调用

1、前言

在UG NX二次开发过程中，有时会遇到形形色色的bug，比如有个读者其采用UG NX二次开发(C++)时，遇到“库缺少需要的入口点”这个问题，看了一下他发给我的源代码，感觉有必要讲一下UG NX二次开发（C++）遇到此类问题的可能情况与解决方法。自然，这是博主的经验之谈，有不足之处还请在评论区讨论。

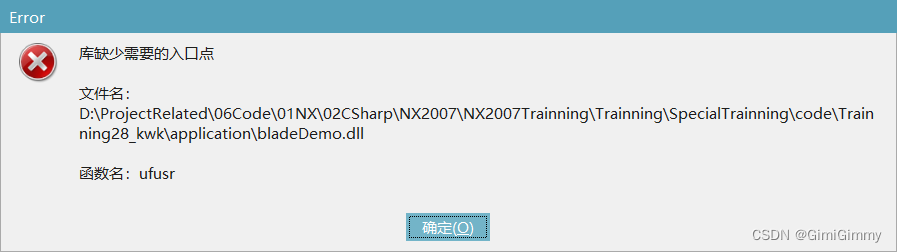
2、“库缺少需要的入口点”错误展示

当我们采用ctrl+U或者点击菜单按钮时，出现的这个错误的提示为：

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/218218.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

C++使用回调函数的两种方式

C++使用回调函数的两种方式

一.函数指针 #include <iostream>typedef void (*callback)(int ,int); class MyTest { public:void setCallback(callback cb){m_callback = cb;}void add(int a, int b){m_callback(a, b);}private:callback m_callback; };void onCallback(int a, int b) {std::cout …
阅读更多...
python每日学11：xpath的使用与调试

python每日学11：xpath的使用与调试

背景&#xff1a;最近在使用selenium 模拟浏览器作一些常规操作&#xff0c;在使用selenium的过程中接触到的一种定位方法&#xff0c;叫xpath, 这里说一下使用心得。 首先&#xff0c;我觉得如果只是简单使用的话是不用详细了解具体的语法规则的。 一、xpath怎么用&#xff1…
阅读更多...
牛客网BC107矩阵转置

牛客网BC107矩阵转置

答案&#xff1a; #include <stdio.h> int main() {int n0, m0,i0,j0,a0,b0;int arr1[10][10]{0},arr2[10][10]{0}; //第一个数组用来储存原矩阵&#xff0c;第二个数组用来储存转置矩阵scanf("%d%d",&n,&m); if((n>1&&n<10)&&am…
阅读更多...
Vue 组件传参 emit

Vue 组件传参 emit

emit 属性&#xff1a;用于创建自定义事件&#xff0c;接收子组件传递过来的数据。 注意&#xff1a;如果自定义事件的名称&#xff0c;和原生事件的名称一样&#xff0c;那么只会触发自定义事件。 setup 语法糖写法请见&#xff1a;《Vue3 子传父 组件传参 defineEmits》 语…
阅读更多...
OxLint 发布了，Eslint 何去何从？

OxLint 发布了，Eslint 何去何从？

由于最近的rust在前端领域的崛起&#xff0c;基于rust的前端生态链遭到rust底层重构&#xff0c;最近又爆出OxLint&#xff0c;是一款基于Rust的linter工具Oxlint在国外前端圈引起热烈讨论&#xff0c;很多大佬给出了高度评价&#xff1b;你或许不知道OxLint&#xff0c;相比ES…
阅读更多...
设计模式——建造者模式（创建型）

设计模式——建造者模式（创建型）

引言 生成器模式是一种创建型设计模式&#xff0c; 使你能够分步骤创建复杂对象。 该模式允许你使用相同的创建代码生成不同类型和形式的对象。 问题 假设有这样一个复杂对象&#xff0c; 在对其进行构造时需要对诸多成员变量和嵌套对象进行繁复的初始化工作。 这些初始化代码…
阅读更多...
《人工智能导论》知识思维导图梳理【第7章节】

《人工智能导论》知识思维导图梳理【第7章节】

文章目录 说明专家系统机器学习机器学习定义工作流程模型评估机器学习分类在这里插入图片描述 机器学习部分md内容机器学习1 机器学习定义机器学习是从数据中自动分析获得模型&#xff0c;并利用模型对未知数据进行预测机器学习&#xff08;machine learning&#xff09;使计算…
阅读更多...
【Python】Flask + MQTT 实现消息订阅发布

【Python】Flask + MQTT 实现消息订阅发布

目录 Flask MQTT 实现消息订阅发布准备开始1.创建Flask项目2创建py文件&#xff1a;mqtt_demo.py3.代码实现4.项目运行 测试1、测试消息接收2、 测试消息发布 扩展 Flask MQTT 实现消息订阅发布 准备 本次项目主要使用到的库&#xff1a;flask_mqtt pip install flask_mqt…
阅读更多...
uniGUI for Delphi UniSweetAlert控件详解

uniGUI for Delphi UniSweetAlert控件详解

UniSweetAlert是UniGUI后期版本新增的一个界面友好的消息提示和输入控件&#xff0c;是ShowMessageN的升级版&#xff0c;UniSweetAlert增加了更多的可控制属性。 属性介绍 1、AlertType&#xff1a;提示类型&#xff0c;分为atError、atSuccess、atInfo、atQuestion、atWarni…
阅读更多...
计算机网络快速刷题

计算机网络快速刷题

自用//奈奎斯特定理和香农定理计算题 参考博客&#xff1a;UDP协议是什么&#xff1f;作用是什么&#xff1f; 肝了&#xff0c;整理了8张图详解ARP原理 【网络协议详解】——FTP系统协议&#xff08;学习笔记&#xff09; 在OSI参考模型中&am…
阅读更多...
RS®SMM100A 矢量信号发生器具备毫米波测试功能的中档矢量信号发生器

RS®SMM100A 矢量信号发生器具备毫米波测试功能的中档矢量信号发生器

R&SSMM100A 矢量信号发生器 具备毫米波测试功能的中档矢量信号发生器 R&SSMM100A 矢量信号发生器在 100 kHz 至 44 GHz 的频率范围内提供优越的射频特性。这款仪器覆盖现有无线标准所使用的 6 GHz 以下的频段、新定义的最高 7.125 GHz 的 5G NR FR1 和 Wi-Fi 6E 频段以…
阅读更多...
Nginx(四层＋七层代理)+Tomcat实现负载均衡、动静分离

Nginx(四层＋七层代理)+Tomcat实现负载均衡、动静分离

一、Tomcat多实例部署 具体步骤请看我之前的博客 写文章-CSDN创作中心https://mp.csdn.net/mp_blog/creation/editor/134956765?spm1001.2014.3001.9457 1.1 访问测试多实例的部署 1.2 分别在三个tomcat服务上部署jsp的动态页面 mkdir /usr/local/tomcat/webapps/test vim …
阅读更多...
stable-diffusion-webui（AI绘画）项目实现，即遇到的问题

stable-diffusion-webui（AI绘画）项目实现，即遇到的问题

实现步骤&#xff1a; 为了使环境中的库版本不会乱&#xff0c;导致自己电脑原来一些项目无法运行最好使用虚拟环境 下载miniconda 在搜索中搜所miniconda找到 建立虚拟环境 conda create --name sdwebui python3.10.6 每次运行激活这个虚拟环境 conda activate sdwebui …
阅读更多...
生产环境_Spark处理轨迹中跨越本初子午线的经度列

生产环境_Spark处理轨迹中跨越本初子午线的经度列

使用spark处理数据集&#xff0c;解决gis轨迹点在地图上跨本初子午线的问题&#xff0c;这个问题很复杂&#xff0c;先补充一版我写的 import org.apache.spark.{SparkConf, SparkContext} import org.apache.spark.sql.{Row, SparkSession} import org.apache.spark.sql.func…
阅读更多...
抖音视频解析，无水印解析下载抖音视频

抖音视频解析，无水印解析下载抖音视频

抖音视频解析&#xff0c;你是否经常遇到这样的情况&#xff0c;看到一些非常精彩的抖音视频&#xff0c;想要保存下来&#xff0c;但因为下载速度慢或者视频带有水印而感到困扰&#xff1f;那么&#xff0c;这款&#xff08;抖音无水印解析工具&#xff09;将是你的得力助手&a…
阅读更多...
JMeter集结点的使用场景以及如何使用？

JMeter集结点的使用场景以及如何使用？

JMeter是一个开源的负载测试工具&#xff0c;它被广泛用于测试应用程序、Web服务和网络协议等的性能。在JMeter中&#xff0c;集结点&#xff08;JMeter Cluster&#xff09;是一种分布式测试环境&#xff0c;它允许多个JMeter实例同时工作来模拟高并发负载。 使用集结点的场景…
阅读更多...
SaaS 电商设计 (五) 私有化部署-实现 binlog 中间件适配

SaaS 电商设计 (五) 私有化部署-实现 binlog 中间件适配

一、 背景 具体的中间件私有化背景在上文 SaaS 电商设计 (二) 私有化部署-缓存中间件适配 已有做相关介绍.这里具体讨论的场景是通过解析mysql binlog 来实现mysql到其他数据源的同步.具体比如:在电商的解决方案业务流中经常有 ES 的使用场景,用以解决一些复杂的查询和搜索商品…
阅读更多...
【答案】2023年国赛信息安全管理与评估第三阶段夺旗挑战CTF（网络安全渗透）

【答案】2023年国赛信息安全管理与评估第三阶段夺旗挑战CTF（网络安全渗透）

【答案】2023年国赛信息安全管理与评估第三阶段夺旗挑战CTF&#xff08;网络安全渗透&#xff09; 全国职业院校技能大赛高职组信息安全管理与评估 &#xff08;赛项&#xff09; 评分标准 第三阶段 夺旗挑战CTF&#xff08;网络安全渗透&#xff09; *竞赛项目赛题* 本文…
阅读更多...
【贝叶斯分析】计算机科学专业博士作业二

【贝叶斯分析】计算机科学专业博士作业二

1 第一题 1.1 题目 已知变量A和B的取值只能为0或1&#xff0c;A⫫&#x1d469;&#xff0c;且&#x1d45d;(&#x1d434;1)0.65&#xff0c;&#x1d45d;(&#x1d435;1)0.77。C的取值与A和B有关&#xff0c;具体关系如下图所表&#xff1a; ABP(C1|A,B)000.1010.99100…
阅读更多...
正则表达式：简化模式匹配的利器

正则表达式：简化模式匹配的利器

正则表达式&#xff1a;简化模式匹配的利器 一、正则表达式简介1.1 正则表达式介绍1.2 正则表达式使用场景 二、正则表达式语法2.1 正则表达式元字符和特性2.2 正则表达式常用匹配 三、正则表达式实战3.1 常见的正则表达式用法3.2 正则表达式的过滤用法3.3 正则表达式的代码用法…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023