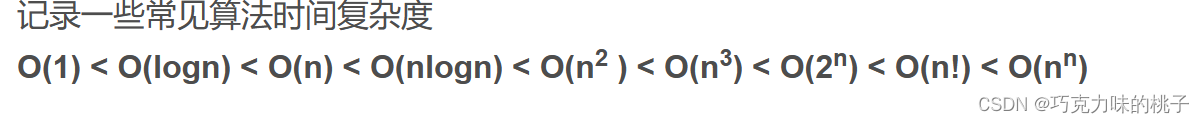目录
顺式存储和链式存储
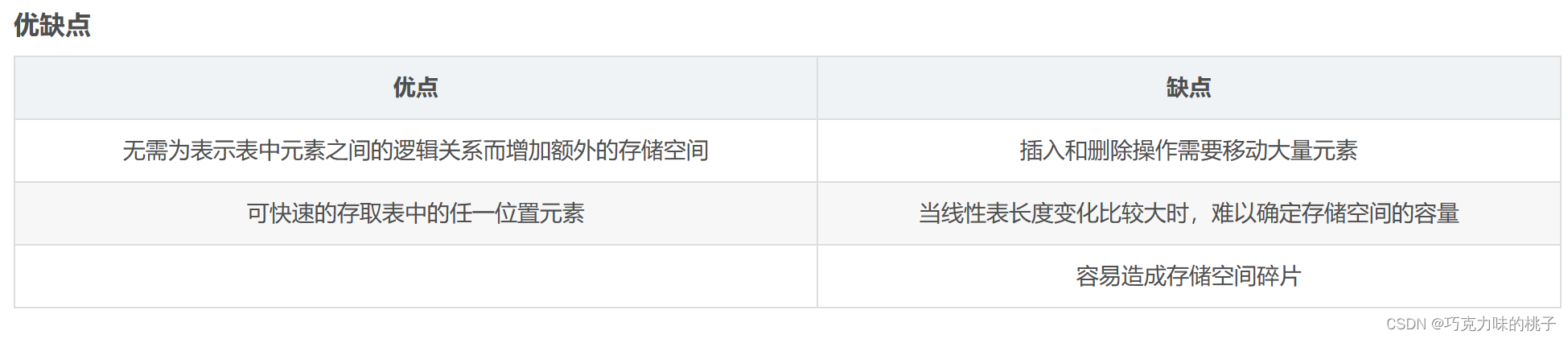
优缺点比较
顺序存储
编辑 链式存储
如何评价哈希函数的好坏
简述哈希查找中链地址法解决冲突的方法
树的遍历
关键路径
完全图
连通图
迪杰斯特拉
b树
特点:
插入(索引不能大于:最大为 M-1 个)
删除(注意索引值不能小于 Math.ceil(M/2)-1 )
情况1(叶子节点且没到最小索引值)
情况2(非叶子节点且破坏最小索引值)
常见的时间复杂度
顺式存储和链式存储
优缺点比较
数据结构之顺序存储与链式存储_顺序存储和链式存储-CSDN博客
顺序存储
 链式存储
链式存储

如何评价哈希函数的好坏


简述哈希查找中链地址法解决冲突的方法
链地址法(Chaining):将具有相同哈希地址的元素(或记录)存储在同一个线性链表中。
建立链表来解决hash冲突,将在同一位置产生hash冲突的元素链接起来组成链表,再将链表插入到hash表中的对应位置。这样一来当我们需要访问查找一个关键字对应的数据时,就需要先通过hash函数获得其索引位置,然后遍历该索引位置对应的链表,逐个节点对关键字key进行比较最终完成查找
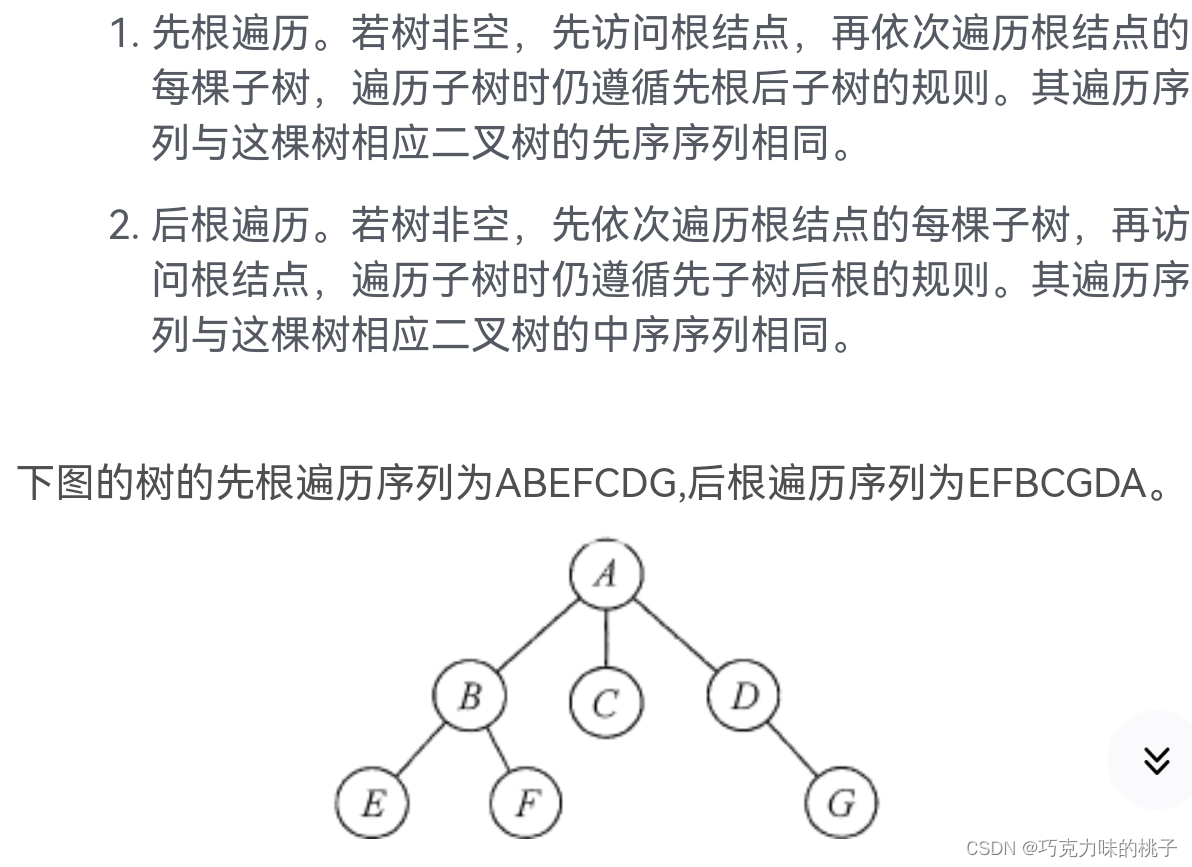
树的遍历
先根遍历 --先序遍历
后根遍历--后序遍历
关键路径
关键活动组成了关键路径,关键路径是图中的最长路径,关键路径长度代表整个工期的最短完成时间,关键活动延期完成,必将导致关键路径长度增加,即整个工期的最短完成时间增加,因此A正确。关键路径并不唯一,当有多条关键路径存在时,其中一条关键路径上的关键活动时间缩短,只能导致本条关键路径变成非关键路径,而无法缩短整个工期,因为其他关键路径没有变化,因此B项不正确。对于A,B两项要搞懂的是,任何一条关键路径上的关键活动变长了,都会使这条关键路径变成更长的关键路径,并且导致其他关键路径变成非关键路径(如果关键路径不唯一),因此整个工期延长。而某些关键活动缩短则不一定缩短整个工期。
C

A

完全图
每两个顶点之间都有边
连通图
N 个顶点的连通图用邻接矩阵表示时,该矩阵至少有2(n-1)个非零元素。
这里肯定是无向图,无向图的邻接矩阵是对称的,所以是边数的两倍
连通图:无向图中,任意两个顶点是连通的(一个顶点不必与另一个顶点直接相连,可以通过其它顶点到达即可)最少有n-1条边
迪杰斯特拉

b树
一棵M阶B树有以下特点。(最多有几个子节点就是当时阶)
特点:
1. 每个结点的值(索引) 都是按递增次序排列存放的,并遵循左小右大原则。
2. 根结点 的 子节点 个数为 [2,M]。
3. 除 根结点 以外的 非叶子结点 的子节点个数 为[ Math.ceil(M/2),M]。 Math.ceil() 为向上取整。
4. 每个非叶子结点的值(索引)个数 = 子节点个数 -1 。最小为 Math.ceil(M/2)-1 最大为 M-1 个。
索引值是指框框里面有多少个数
5. B树的所有叶子结点都位于同一层。
下图是一个 3阶B树:

可以看到:
1. 除 根结点 外,所有 非叶子结点 都至少有 M/2 = 1.5 取整 = 2 个结点。
2. 每个 结点中 的索引值 都是从小到大排序的。
3. 所有叶子结点都在同一层中。
插入(索引不能大于:最大为 M-1 个)
1.插入时,超过索引值就要分裂,中间是元素往上提(塞到父亲结点那里)旁边的元素分裂,各自形成两个小圈圈 (最大值为阶数-1)
2.父亲节点满了也往上塞

删除(注意索引值不能小于 Math.ceil(M/2)-1 )
情况1(叶子节点且没到最小索引值)
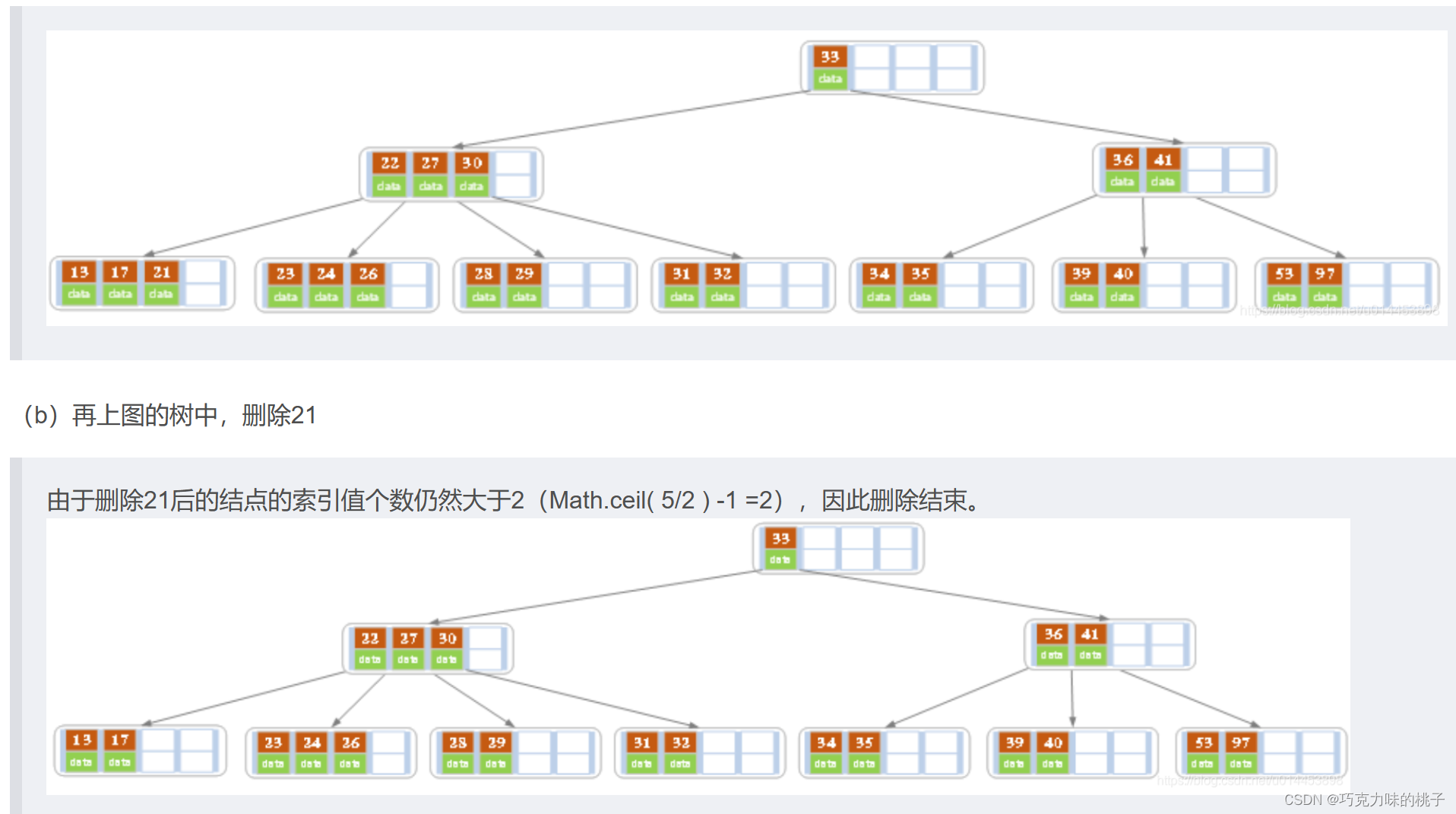
情况2(非叶子节点且破坏最小索引值)
27 1.先找到后继代替他
2.找到子节点(索引值最多)的索引值中最大数移到 28的位置,将28移到以前的位置(少了索引值)。

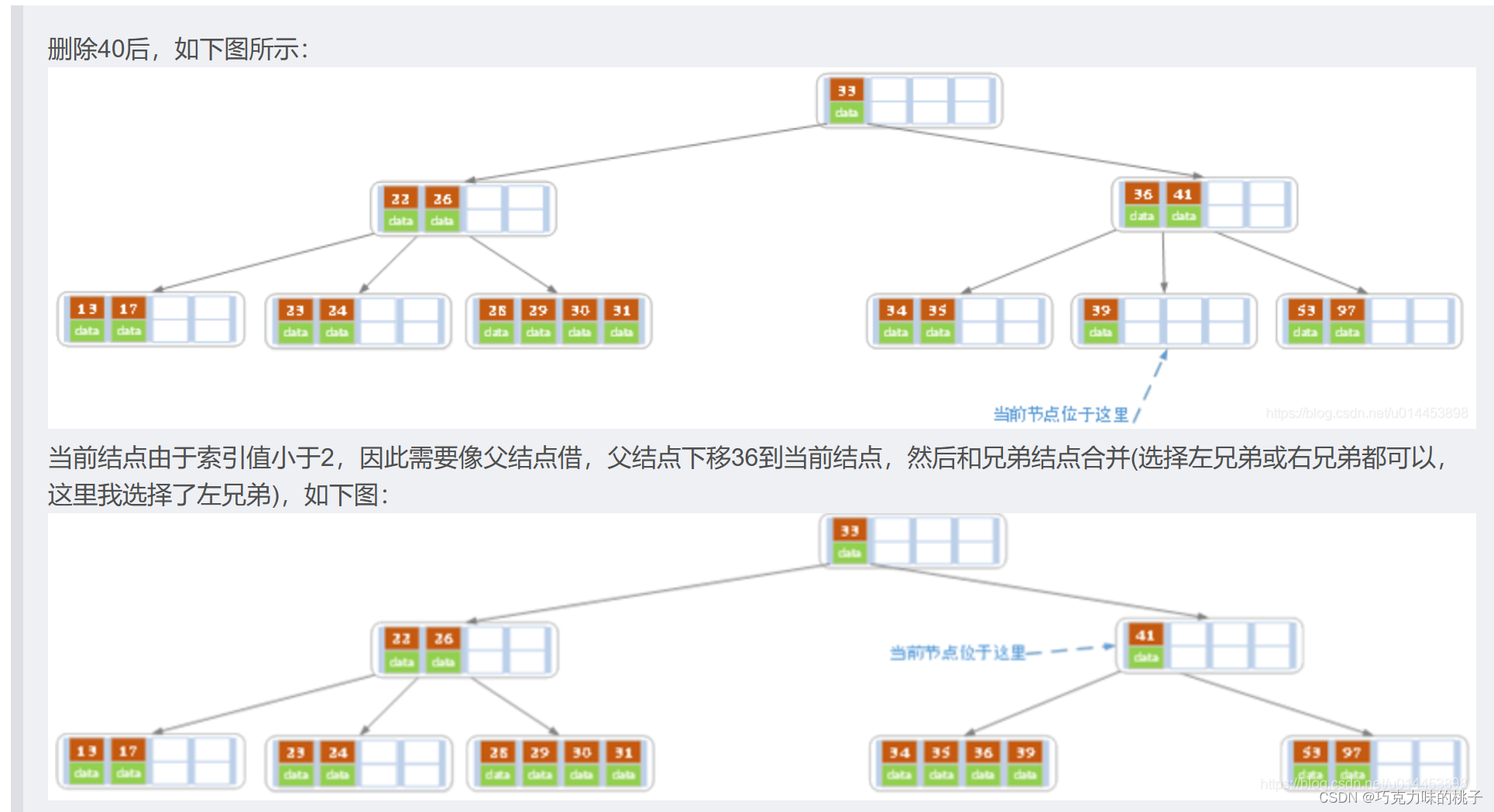
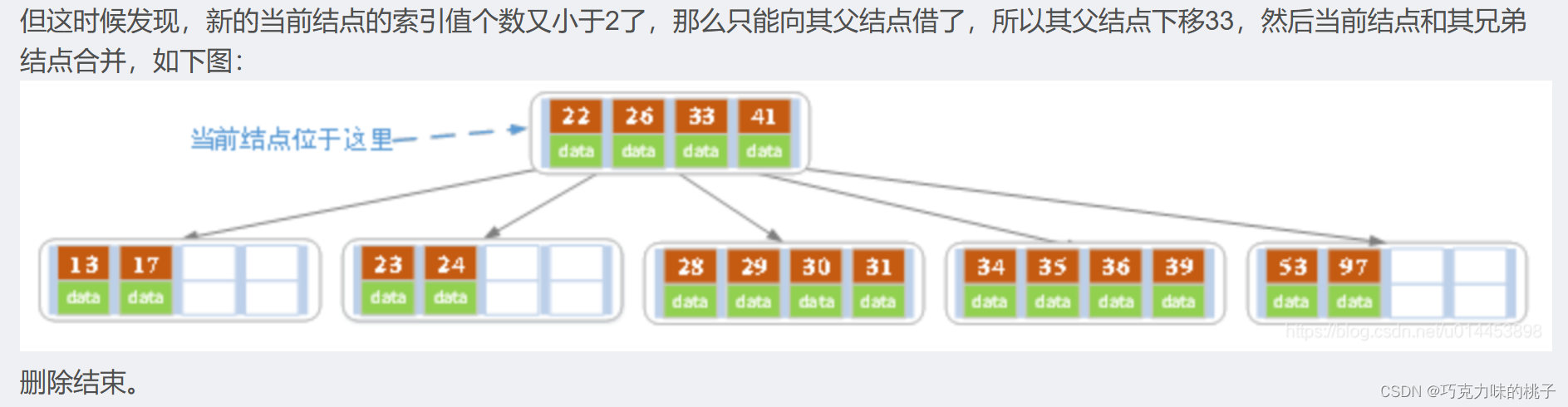
情况3(兄弟也没有多的,找父亲借)

B树和B+树_b+树的叶子结点本身是按照什么排序-CSDN博客
常见的时间复杂度