leetcode 236. 二叉树的最近公共祖先
题目
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
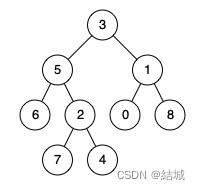
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
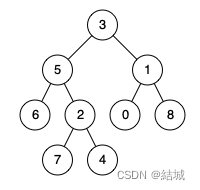
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
思路
一开始我是想着正常递归遍历,然后记录一下搜索路径,然后遇到p或者q就记录找到了(flag=true)然后一直回退就完了。但是需要注意递归结束要remove的,否则记录的是递归顺序而不是从根节点到当前的搜索顺序。remove前的if(flag)也很重要,这表示找到了,就别remove了。然后对比p和q的路径就完了。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {boolean flag = false;public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {List<TreeNode> pList = new ArrayList<TreeNode>();List<TreeNode> qList = new ArrayList<TreeNode>();dfs(root, pList, p);flag = false;dfs(root, qList, q);TreeNode res = new TreeNode();for (int i=0;i<Math.min(pList.size(), qList.size());i++) {if (pList.get(i) == qList.get(i)) {res = pList.get(i);}else {break;}}return res;}public void dfs(TreeNode root, List<TreeNode> list, TreeNode node) {if (flag || root == null) {list.add(null);return;}list.add(root);if (root == node) {flag = true;return;}dfs(root.left, list, node);if (flag) {return;}list.remove(list.size() - 1);dfs(root.right, list, node);if (flag) {return;}list.remove(list.size() - 1);}
}
但这个结果太拉了,其实是有更好的方法的。那就是p和q往上递归搜索,找到同一个节点就结束了。其实这就是后续遍历的用处,左右中。
这里我们来聊聊递归的写法细节,首先肯定我们知道是先写一个判断递归中止的函数。那其他的呢有没有返回值怎么判断,这里可以告诉大家:
1 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。
2 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。
3 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。
2的写法是
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
3的写法是
left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中
在递归函数有返回值的情况下:如果要搜索一条边,递归函数返回值不为空的时候,立刻返回,如果搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。
代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == p || root == q || root == null) {return root;}TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if (left != null && right != null) {return root;}else if (left == null) {return right;}else if (right == null) {return left;}else {return null;}}
}