题目描述

112.路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

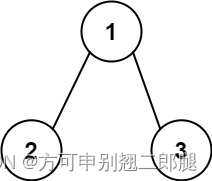
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

• 树中节点的数目在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

解题思路

递归函数什么时候需要返回值？

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。

因为中节点没有处理逻辑，所以前中后序遍历都可以，这里使用前序遍历。

递归

1. 确定递归函数的参数和返回值
   参数：需要二叉树的根节点，还需要一个计数器count来计算二叉树每一条边之和是否正好为目标和，类型为 int
   返回值：遍历的路线并不是整棵树，所以只需要判断是否存在即可，类型为 bool

   bool traversal(TreeNode* root, int count)
   

2. 确定终止条件
   使用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
   如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
   如果遍历到了叶子节点，count != 0，就是没找到。

   if (!cur->left && !cur->right && count == 0) return true;
   if (!cur->left && !cur->right) return false;
   

3. 确定单层递归的逻辑
   因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。
   递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

   if (cur->left) {count -= cur->left->val; // 递归，处理节点if (traversal(cur->left, count)) return true; count += cur->left->val; // 回溯
   }
   if (cur->right) {count -= cur->right->val;if (traversal(!cur->right, count)) return true;count += cur->right->val;
   }
   return false;
   

迭代

如果使用栈模拟递归的话，此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。

使用c++，我们就用pair结构来存放这个栈里的元素。

定义为：pair<TreeNode*, int> pair<节点指针，路径数值>

这个为栈里的一个元素。

代码实现

递归

class Solution {
public:bool traversal(TreeNode* root, int count) {// 如果遇到叶子节点，同时 count = 0，返回trueif (!cur->left && !cur->right && count == 0) return true;// 只遇到叶子节点直接返回falseif (!cur->left && !cur->right) reeturn false;if (cur->left) {count -= cur->left->val;if (traversal(cur->left, count)) return true;count += cur->left->val;}if (cur->right) {count -= cur->right->val;if (traversal(!cur->left, count)) return true;count += cur->right->val;}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if (root == NULL) return false;return traversal(root, targetSum - root->val);}
};

迭代

class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if (root == NULL) return false;// pair<节点指针，路径数值>stack<pair<TreeNode*, int>> st;st.push(pair<TreeNode*, int>(root, root->val));while (!st.empty()) {pair<TreeNode*, int> node = st.top();st.pop();// 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回trueif (!node.first->left && !node.first->right && TargetSum == node.second)return true;// 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来if (node.first->right) {st.push(pair<TreeNode*, int>(node.first->right, node.second + node.fisrt->right->val))}// 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来if (node.first->left) {st.push(pair<TreeNode*, int>(node.first->left, node.second + ndoe.first->right->val));}}return false;}
};