遗传算法应用-- 栅格法机器人路径规划

文章目录

  • 一、遗传算法
    • 1.1 编码与解码
    • 1.2 选择算子-轮盘赌法
    • 1.3 交叉算子
    • 1.4 变异算子
    • 1.5 遗传算法流程
    • 1.6 基于遗传算法的栅格法机器人路径规划
  • 二、采用模拟退火算法改善适应度函数

一、遗传算法

遗传算法 (Genetic AIgorithm, 简称 GA)起源于对生物系统所进行的计算机模拟研究，是一种随机全局搜索优化方法，它模拟了自然选择和遗传中发生的复制、交叉 (crossover) 和变异 (mutation)现象，从任一初始种群 (PopuIation) 出发，通过随机选择、交叉和变异操作，产生一群更适合环境的个体，使群体进化到搜索空间中越来越好的区域，这样一代一代不断繁衍进化，最后收敛到一群最适应环境的个体(lndividual) ，从而求得问题的优质解。

1.1 编码与解码

实现遗传算法的第一步就是明确对求解问题的编码和解码方式。所谓编码就是把要传递的信息按照一定的规则进行组织，所谓解码就是把收到的信息按照一定的规则进行解忻，且这个规则必须是编码者和解码者事先都知道或约定好的。

对于函数优化问题，一般有两种编码方式，各具优缺点

  • 实数编码：直接用实数表示基因，容易理解且不需要解码过程、但容易过早收敛，从而陷入局部最优
  • 二进制编码：稳定性高，种群多样性大，需要的存储空间大，需要解码且难以理解。

1.2 选择算子-轮盘赌法

在这里插入图片描述
轮盘赌选择法是依据个体的适应度值计算每个个体在子代中出现的概率，并按照此概率随机选择个体构成子代种群，因此该方法也被称为适应度比例法。轮盘赌选择策略的出发点是适应度值越好的个体被选择的概率越大。因此，在求解最大化问题的时候，我们可以直接采用适应度值来进行选择。但是在求解最小化问题的时候，我们必须首先将问题的适应度函数进行转换(如采用倒数或相反数)以将问题转化为最大化问题。

1.3 交叉算子

交叉操作是指从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体。体现了信息交换的思想。在实际应用中，使用率最高的是单点交叉算子，该算子在配对的染色体中随机的选择一个交叉位置，然后在该交叉位置对配对的染色体进行基因位变。其他交叉算子包括：双点交叉或多点交叉，均匀交叉，算术交叉。

1.4 变异算子

对种群中的每一个个体，以变异概率改变一个或多个基因座上的基因值为其他的等位基因。同生物界中一样，变异发生的概率很低，变异为新个体的产生了机会。

变异率一般可取0.001~0.1。变异率不能取得太大，如果大于0.5，遗传算法就会退化为随机搜索。

1.5 遗传算法流程

  • 对于一个实际问题，首先通过编码将解空间的数据表示为基因型串结构
  • 然后进行种群初始化，随机产生N个初始串结构数据，每个串结构数据称为一个个体，N个个体构成了一个群体。
  • 适应度表明个体或解的优劣性。
  • 选择的原则是适应性强的个体，为下一代贡献一个或多个后代的概率大。
  • 交叉操作可以得到新一代个体，新个体组合体现了其父辈个体的特性。
  • 变异过程以一定的概率随机地改变串结构数据中某个串的值。
  • 新种群满足条件时，停止进化。

1.6 基于遗传算法的栅格法机器人路径规划

机器人控制过程中，路径规划是其中重要的一环。因此本文采用遗传算法对机器人移动时的路径进行优化，最终选取出一条最优路径。采用栅格图法为机器人移动的地图进行建模，并根据遗传算法机理，在MATLAB上仿真实现了最优路径的选取。

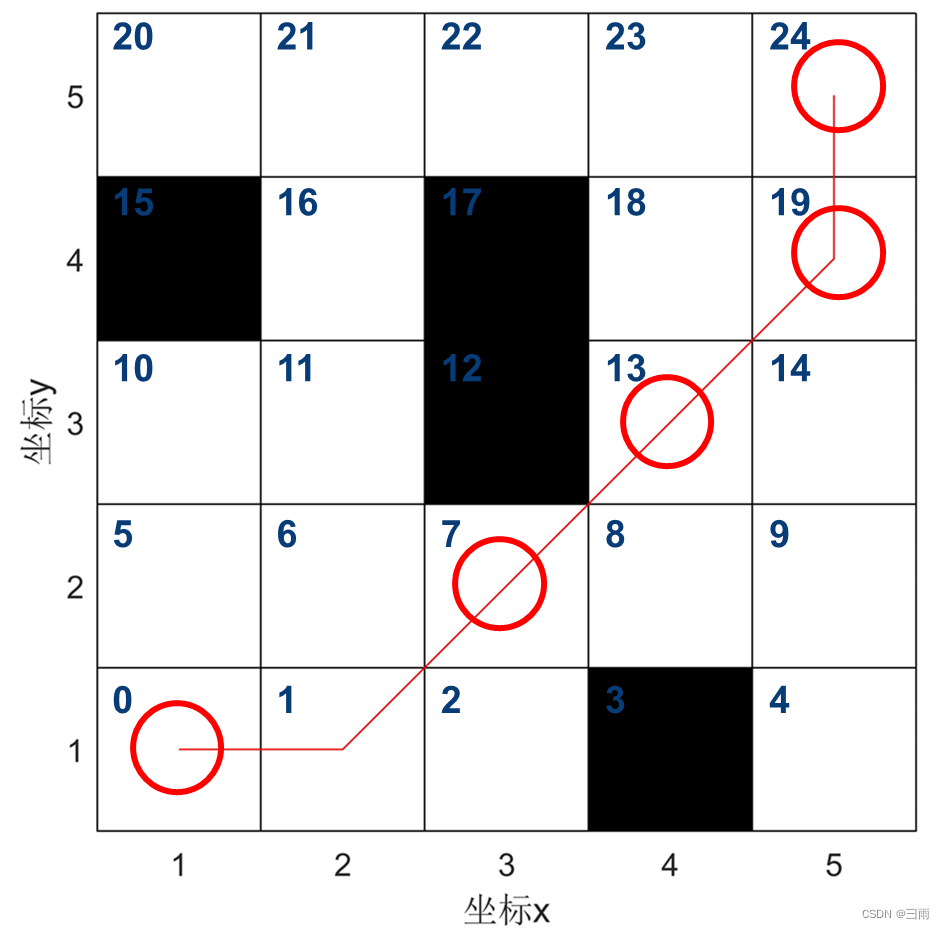
首先对其进行编码，用0~24表示每个方格，如图所示路径编码为(0,1,7,13,19,24)。

种群初始化

  • 每行选择一个栅格
  • 判断相邻栅格是否连续
  • 不连续时进行插入栅格操作，直到连续

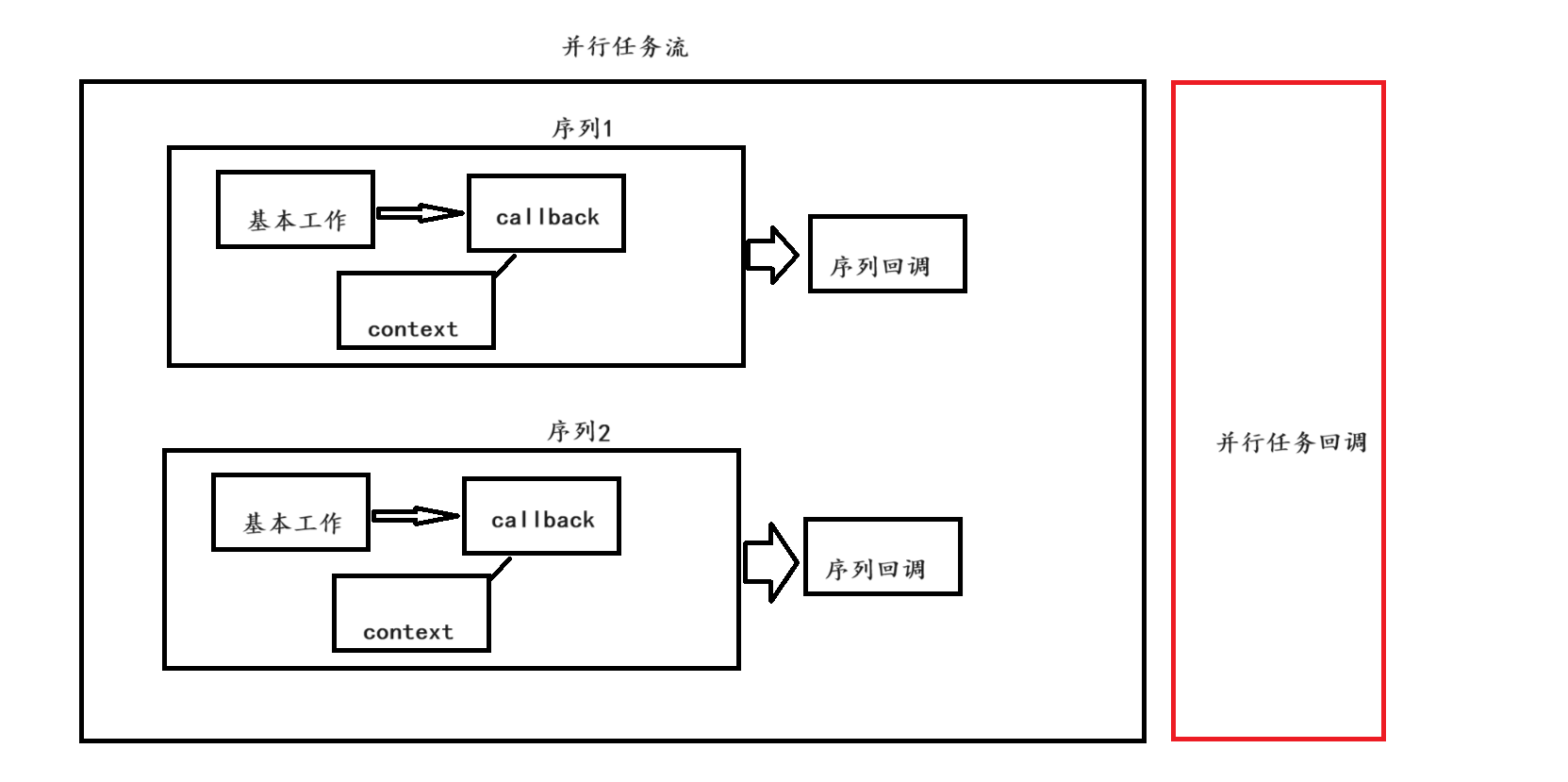
选择：如图所示有①②两条路径，对应两个个体。选择路径长度和路径平滑性作为评价指标：

交叉：如上图所示有①②两条路径，对应两个个体。通过交换交叉点前后的路径可形成新的路径。

变异：随机选择路径中的两个栅格。 采用种群初始化中的方法在两个栅格间产生新路径。

main

% 基于遗传算法的栅格法机器人路径规划
clc;
clear;
% 输入数据,即栅格地图
G=  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 0 0;0 1 1 1 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0;0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0;0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0;0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
%G = [0 0 0 1 0;
%     0 0 0 0 0;
%     0 0 1 0 0;
%     1 0 1 0 0;
%     0 0 0 0 0;];p_start = 0;   % 起始序号
p_end = 399;   % 终止序号
NP = 200;      % 种群数量
max_gen = 50;  % 最大进化代数
pc = 0.8;      % 交叉概率
pm = 0.2;      % 变异概率
%init_path = [];
z = 1;  
new_pop1 = {}; % 元包类型路径
[y, x] = size(G);
% 起点所在列（从左到右编号1.2.3...）
xs = mod(p_start, x) + 1; 
% 起点所在行（从上到下编号行1.2.3...）
ys = fix(p_start / x) + 1;
% 终点所在列、行
xe = mod(p_end, x) + 1;
ye = fix(p_end / x) + 1;% 种群初始化step1，必经节点,从起始点所在行开始往上，在每行中挑选一个自由栅格，构成必经节点
pass_num = ye - ys + 1;
pop = zeros(NP, pass_num);
for i = 1 : NPpop(i, 1) = p_start;j = 1;% 除去起点和终点for yk = ys+1 : ye-1j = j + 1;% 每一行的可行点can = []; for xk = 1 : x% 栅格序号no = (xk - 1) + (yk - 1) * x;if G(yk, xk) == 0% 把点加入can矩阵中can = [can no];endendcan_num = length(can);% 产生随机整数index = randi(can_num);% 为每一行加一个可行点pop(i, j) = can(index);endpop(i, end) = p_end;%pop% 种群初始化step2将上述必经节点联结成无间断路径single_new_pop = generate_continuous_path(pop(i, :), G, x);%init_path = [init_path, single_new_pop];if ~isempty(single_new_pop)new_pop1(z, 1) = {single_new_pop};z = z + 1;end
endmean_path_value = zeros(1, max_gen);
min_path_value = zeros(1, max_gen);
% 循环迭代操作
for i = 1 : max_gen% 计算适应度值% 计算路径长度path_value = cal_path_value(new_pop1, x)% 计算路径平滑度path_smooth = cal_path_smooth(new_pop1, x)fit_value = 1 .* path_value .^ -1 + 1 .* path_smooth .^ -1;mean_path_value(1, i) = mean(path_value);[~, m] = max(fit_value);min_path_value(1, i) = path_value(1, m);% 选择操作new_pop2 = selection(new_pop1, fit_value);% 交叉操作new_pop2 = crossover(new_pop2, pc);% 变异操作new_pop2 = mutation(new_pop2, pm, G, x);% 更新种群new_pop1 = new_pop2;end
% 画每次迭代平均路径长度和最优路径长度图
figure(1)
plot(1:max_gen,  mean_path_value, 'r')
hold on;
plot(1:max_gen, min_path_value, 'b')
legend('平均路径长度', '最优路径长度');
min_path_value(1, end)
% 在地图上画路径
[~, min_index] = max(fit_value);
min_path = new_pop1{min_index, 1};
figure(2)
hold on;
title('遗传算法机器人运动轨迹'); 
xlabel('坐标x'); 
ylabel('坐标y');
DrawMap(G);
[~, min_path_num] = size(min_path);
for i = 1:min_path_num% 路径点所在列（从左到右编号1.2.3...）x_min_path(1, i) = mod(min_path(1, i), x) + 1; % 路径点所在行（从上到下编号行1.2.3...）y_min_path(1, i) = fix(min_path(1, i) / x) + 1;
end
hold on;
plot(x_min_path, y_min_path, 'r')

selection

% 用轮盘赌法选择新的个体
% 输入变量：pop元胞种群，fitvalue：适应度值
% 输出变量：newpop选择以后的元胞种群
function [new_pop] = selection(pop, fit_value)
%构造轮盘
[px, ~] = size(pop);
total_fit = sum(fit_value);
p_fit_value = fit_value / total_fit;
p_fit_value = cumsum(p_fit_value);    % 概率求和
% 随机数从小到大排列
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= pxif(ms(newin)) < p_fit_value(fitin)new_pop{newin, 1} = pop{fitin, 1};newin = newin+1;elsefitin = fitin+1;end
end

mutation

% 变异操作
% 函数说明
% 输入变量：pop：种群，pm：变异概率
% 输出变量：newpop变异以后的种群
function [new_pop] = mutation(pop, pm, G, x)
[px, ~] = size(pop);
new_pop = {};
for i = 1:px% 初始化最大迭代次数max_iteration = 0;single_new_pop = pop{i, 1};[~, m] = size(single_new_pop);% single_new_pop_slice初始化single_new_pop_slice = [];if(rand < pm)while isempty(single_new_pop_slice)% 生成2-（m-1）的两个随机数,并排序mpoint = sort(round(rand(1,2)*(m-3)) + [2 2]);single_new_pop_slice = [single_new_pop(mpoint(1, 1)-1) single_new_pop(mpoint(1, 2)+1)];single_new_pop_slice = generate_continuous_path(single_new_pop_slice, G, x);%max_iteration = max_iteration + 1;if max_iteration >= 100000breakendendif max_iteration >= 100000new_pop{i, 1} = pop{i, 1};elsenew_pop{i, 1} = [single_new_pop(1, 1:mpoint(1, 1)-1), single_new_pop_slice(2:end-1), single_new_pop(1, mpoint(1, 2)+1:m)];end% single_new_pop_slice再次初始化single_new_pop_slice = [];elsenew_pop{i, 1} = pop{i, 1};end
end

generate_continuous_path

% 将必经节点联结成无间断路径
function [single_new_pop] = generate_continuous_path(single_pop, G, x)
i = 1;
single_new_pop = single_pop;
[~, single_path_num] = size(single_new_pop);
while i ~= single_path_num% 点i所在列（从左到右编号1.2.3...）x_now = mod(single_new_pop(1, i), x) + 1; % 点i所在行（从上到下编号行1.2.3...）y_now = fix(single_new_pop(1, i) / x) + 1;% 点i+1所在列、行x_next = mod(single_new_pop(1, i + 1), x) + 1;y_next = fix(single_new_pop(1, i + 1) / x) + 1;% 初始化最大迭代次数max_iteration = 0;% 判断点i和i+1是否连续,若不连续插入值while max(abs(x_next - x_now), abs(y_next - y_now)) > 1x_insert = floor((x_next + x_now) / 2);y_insert = floor((y_next + y_now) / 2);% 插入栅格为自由栅格if G(y_insert, x_insert) == 0  % 栅格序号num_insert = (x_insert - 1) + (y_insert - 1) * x;% 插入新序号single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];% 插入栅格为障碍物栅格else   % 往左走if G(y_insert, x_insert - 1) == 0 && ((x_insert - 2) + (y_insert - 1) * x ~= single_new_pop(1, i)) && ((x_insert - 2) + (y_insert - 1) * x ~= single_new_pop(1, i+1))x_insert = x_insert - 1;% 栅格序号num_insert = (x_insert - 1) + (y_insert - 1) * x;% 插入新序号single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];% 往右走    elseif G(y_insert, x_insert + 1) == 0 && (x_insert + (y_insert - 1) * x ~= single_new_pop(1, i)) && (x_insert + (y_insert - 1) * x ~= single_new_pop(1, i+1))x_insert = x_insert + 1;% 栅格序号num_insert = (x_insert - 1) + (y_insert - 1) * x;% 插入新序号single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];% 向上走elseif G(y_insert + 1, x_insert) == 0 && ((x_insert - 1) + y_insert * x ~= single_new_pop(1, i)) && ((x_insert - 1) + y_insert * x ~= single_new_pop(1, i+1))y_insert = y_insert + 1;% 栅格序号num_insert = (x_insert - 1) + (y_insert - 1) * x;% 插入新序号single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];% 向下走elseif  G(y_insert - 1, x_insert) == 0 && ((x_insert - 1) + (y_insert - 2) * x ~= single_new_pop(1, i)) && ((x_insert - 1) + (y_insert-2) * x ~= single_new_pop(1, i+1))y_insert = y_insert - 1;% 栅格序号num_insert = (x_insert - 1) + (y_insert - 1) * x;% 插入新序号single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];% 其他情况舍去此路径else%break_pop = single_new_popsingle_new_pop = [];breakend    endx_next = x_insert;y_next = y_insert;max_iteration = max_iteration + 1;if max_iteration > 20000single_new_pop = [];breakendendif isempty(single_new_pop)breakend[~, single_path_num] = size(single_new_pop);i = i + 1;
end

DrawMap

%创建具有障碍物的栅格地图
%矩阵中1代表黑色栅格function G = DrawMap(G)
b = G;
b(end+1,end+1) = 0;
colormap([1 1 1;0 0 0]);  % 创建颜色
pcolor(0.5:size(G,2) + 0.5, 0.5:size(G,1) + 0.5, b); % 赋予栅格颜色
set(gca, 'XTick', 1:size(G,1), 'YTick', 1:size(G,2));  % 设置坐标
axis image xy;  % 沿每个坐标轴使用相同的数据单位，保持一致

crossover

%交叉变换
%输入变量：pop：父代种群，pc：交叉的概率
%输出变量：newpop：交叉后的种群
function [new_pop] = crossover(pop, pc)
[px,~] = size(pop);
% 判断路径点数是奇数或偶数
parity = mod(px, 2);
new_pop = {};
for i = 1:2:px-1singal_now_pop = pop{i, 1};singal_next_pop = pop{i+1, 1};[lia, lib] = ismember(singal_now_pop, singal_next_pop);[~, n] = find(lia == 1);[~, m] = size(n);if (rand < pc) && (m >= 3)% 生成一个2-m-1之间的随机数r = round(rand(1,1)*(m-3)) +2;crossover_index1 = n(1, r);crossover_index2 = lib(crossover_index1);new_pop{i, 1} = [singal_now_pop(1:crossover_index1), singal_next_pop(crossover_index2+1:end)];new_pop{i+1, 1} = [singal_next_pop(1:crossover_index2), singal_now_pop(crossover_index1+1:end)];elsenew_pop{i, 1} =singal_now_pop;new_pop{i+1, 1} = singal_next_pop;end
if parity == 1new_pop{px, 1} = pop{px, 1};
end
end

cal_path_value

% 计算路径长度函数
function [path_value] = cal_path_value(pop, x)
[n, ~] = size(pop);
path_value = zeros(1, n);
for i = 1 : nsingle_pop = pop{i, 1};[~, m] = size(single_pop);for j = 1 : m - 1% 点i所在列（从左到右编号1.2.3...）x_now = mod(single_pop(1, j), x) + 1; % 点i所在行（从上到下编号行1.2.3...）y_now = fix(single_pop(1, j) / x) + 1;% 点i+1所在列、行x_next = mod(single_pop(1, j + 1), x) + 1;y_next = fix(single_pop(1, j + 1) / x) + 1;if abs(x_now - x_next) + abs(y_now - y_next) == 1path_value(1, i) = path_value(1, i) + 1;elsepath_value(1, i) = path_value(1, i) + sqrt(2);endend
end

cal_path_smooth

% 计算路径平滑度函数
function [path_smooth] = cal_path_smooth(pop, x)
[n, ~] = size(pop);
path_smooth = zeros(1, n);
for i = 1 : nsingle_pop = pop{i, 1};[~, m] = size(single_pop);for j = 1 : m - 2% 点i所在列（从左到右编号1.2.3...）x_now = mod(single_pop(1, j), x) + 1; % 点i所在行（从上到下编号行1.2.3...）y_now = fix(single_pop(1, j) / x) + 1;% 点i+1所在列、行x_next1 = mod(single_pop(1, j + 1), x) + 1;y_next1 = fix(single_pop(1, j + 1) / x) + 1;% 点i+2所在列、行x_next2 = mod(single_pop(1, j + 2), x) + 1;y_next2 = fix(single_pop(1, j + 2) / x) + 1;% cos A=(b?+c?-a?)/2bcb2 = (x_now - x_next1)^2 + (y_now - y_next1)^2;c2 = (x_next2 - x_next1)^2 + (y_next2 - y_next1)^2;a2 = (x_now - x_next2)^2 + (y_now - y_next2)^2;cosa = (c2 + b2 - a2) / (2 * sqrt(b2) *  sqrt(c2));angle = acosd(cosa);if angle < 170 && angle > 91path_smooth(1, i) = path_smooth(1, i) + 3;elseif angle <= 91 && angle > 46path_smooth(1, i) = path_smooth(1, i) + 15;elseif angle <= 46path_smooth(1, i) = path_smooth(1, i) + 20;endend
end

运行效果：
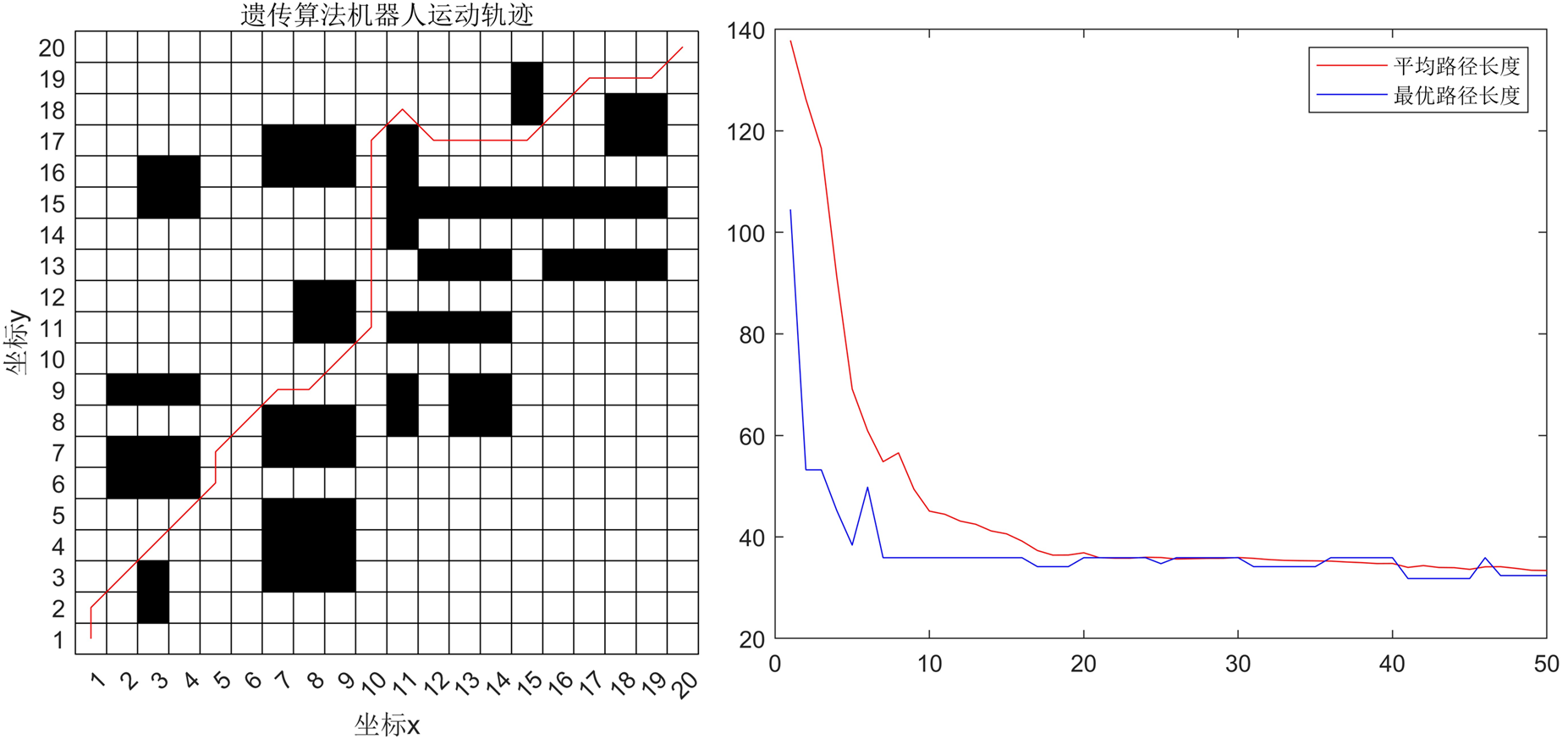
在这里插入图片描述

二、采用模拟退火算法改善适应度函数

为了提高遗传算法运行效率和求解质量，这里引入模拟退火算法的思想，模拟退火(Stimulated Annealing, SA)具有较强的局部寻优能力，并能使搜索过程避免陷入局部最优解，采用模拟退火遗传算法（Stimulated Annealing Genetic Algorithm，SAGA）求解路径优化问题。

模拟退火遗传算法是对适应度函数的改进，在前期（高温）减少个体间的适应度差异，后期（低温）放大个体间适应度差异，突出优秀个体，完成适应度拉伸的作用，在一定程度上弥补了遗传算法在前期容易早熟、后期容易停滞的缺点。
具体的适应度值计算公式如下所示：

其中， M M M为种群大小， f i f_i fi​为第𝑖个个体的适应度， g g g为遗传代数， T T T为温度， T 0 T_0 T0​为初始温度， A A A为退火速度（本文取 T 0 = 100 , A = 0.8 T_0 = 100, A = 0.8 T0​=100,A=0.8）

SAGA_main

%%%%%%模拟退火遗传算法(SAGA)%%%%%%%%%%%
clc;
clear;
%%%设置超参数
p_crs = 0.7;   %交叉概率
p_mut = 0.1;   %变异概率
ratio = 0.5;   %选择操作中父辈的比例
pop_num = 5000;  %种群规模
chrom_len = 7;  %染色体长度，这里代表路线的点数
iteration = 40;
T0 = 100;  %初始温度
A = 0.8;  %退火速度% 一个个体就是一条路线
[x,y]=popinit(pop_num,chrom_len);   %产生初始种群   
fit=saga_fitness(x,y, T0);      %计算种群适应度
[bestx0,besty0,fit0]=best(x,y,fit); 
d0 = 0; %初始路径长度
for j=1:1:size(bestx0,2)-1d0 = d0 + sqrt((bestx0(1,j+1)-bestx0(1,j)).^2 + ...(besty0(1,j+1)-besty0(1,j)).^2);     %该个体（即路线）的路径长度
endfor i=1:1:iteration           %设置进化代数[Parentx,Parenty]=select(x, y, fit, ratio);      %选择[Kidx,Kidy]=crossover(Parentx,Parenty,p_crs);       %交叉[Kidx,Kidy]=mutation(Kidx,Kidy,p_mut);              %变异x = [Parentx; Kidx];    % 得到新的种群y = [Parentx; Kidy];x(:,chrom_len)=1.5;   % 保留终点y(:,chrom_len)=8.9;T = T0 * A^(i-1);  % 当前温度fit = saga_fitness(x,y,T);   % 计算进化后的适应度[bestx,besty,bestfit]=best(x,y,fit);   %选择每一代中的最佳个体route_x(i,:)=bestx;                     %保存该最佳个体route_y(i,:)=besty;route_fit(i)=bestfit;for j=1:1:size(bestx,2)-1dd(j)=sqrt((bestx(1,j+1)-bestx(1,j)).^2 + ...(besty(1,j+1)-besty(1,j)).^2);     %该个体（即路线）的路径长度endd(i) = sum(dd);   %有问题fprintf('%dth 代进化完成...\n', i)
%     plot(bestx,besty,'r-');
end
route_fit = [fit0, route_fit];   %加上初始种群中最优个体
route_x = [bestx0; route_x];
route_y = [bestx0; route_y];
d = [d0, d];[final_fit,idx]=max(route_fit);            %所有代中的的最佳路线
final_routex=route_x(idx,:);
final_routey=route_y(idx,:);
final_distance = min(d)             %最佳路径长度%==========画图，可视化路线、进化过程==============
% start point
xs=0;
ys=0;
% Destination
xt=1.5;
yt=8.9;
%obstacle
xobs=[1.5 4.0 1.2];
yobs=[6.5 3.0 1.5];
robs=[1.5 1.0 0.8];
theta=linspace(0,2*pi,100);
max_area = 0;
for k=1:numel(xobs)fill(xobs(k)+robs(k)*cos(theta),yobs(k)+robs(k)*sin(theta),[0.5 0.7 0.8]);  % 后一个参数表示RGB值text(xobs(k), yobs(k), num2str(k))hold on;
end
plot(xs,ys,'bs','MarkerSize',12,'MarkerFaceColor','y');
plot(xt,yt,'kp','MarkerSize',16,'MarkerFaceColor','g');
grid on;
hold on;%%画出最短路径的路线
plot(final_routex,final_routey,'r*-',  'linewidth', 1.5);
legend('障碍物1','障碍物2','障碍物3','起点', '终点', '最短路线')
set(gca,'FontSize',16);
hold off;% 进化过程中适应度曲线
figure,
% plot(0:1:size(route_fit,2)-1, route_fit, 'linewidth', 1.2)
plot(d, 'linewidth', 1.2)
% ylim([0.08,0.1])
title(['变异率=',num2str(p_mut),',交叉率=', num2str(p_crs), '的进化曲线']);
legend('最短路径长度值', 'Location', 'northeast');
set(gca,'FontSize',16);d_saga = d;
save('d_saga');load('d_ga.mat');
figure,
plot(d, 'linewidth', 1.2), hold on,
plot(d_ga, 'linewidth', 1.2);
title(['变异率=',num2str(p_mut),',交叉率=', num2str(p_crs), '的进化曲线']);
legend('SAGA最优路径值', 'GA最优路径值', 'Location', 'northeast');
set(gca,'FontSize',16);

select

%====================================
%%输入参数：种群、其适应度、选择比例
%%输出参数：父辈种群——x,y横纵坐标
%%说明：
%     按照输入参数的比例，从种群中选择父代
%====================================
function [parentPopx, parentPopy]=select(popx, popy, fitness, ratio)totalfit=sum(fitness); %适应值之和accP=cumsum(fitness/totalfit); %概率累计和%轮盘赌选择算法for n=1:round(ratio*size(popx,1))mat=find(accP>rand); %找到比随机数大的累积概率if isempty(mat)continueendparentPopx(n,:)=popx(mat(1),:);%将首个比随机数大的累积概率的位置的个体遗传下去parentPopy(n,:)=popy(mat(1),:);end
end

saga_fitness

%====================================
%%输入参数：种群——x,y横纵坐标, 当前温度T
%%输出参数：种群中每个个体的适应度值
%%说明：
%     逐个计算种群中个体的适应度值，判断该个体所连成线路与圆形障碍物之间的关系，
%     将满足条件的路径的距离倒数作为适应度值
%====================================function fitval=saga_fitness(x,y,T)%obstaclexobs=[1.5 4.0 1.2];yobs=[6.5 3.0 1.5];robs=[1.5 1.0 0.8];[n, xn] = size(x);for i=1:1:ncnt_line = 0;  %记录穿过障碍物的线段数%%拆分相邻的两个点，便于后续计算for m=1:1:xn-1x1(m)=x(i,m);y1(m)=y(i,m);endfor n=2:1:xnx2(n-1)=x(i,n);y2(n-1)=y(i,n);end%%判断线段与障碍物的关系for m = 1:size(x1,2)A = y2(m) - y1(m);B = x1(m) - x2(m);C = y1(m)*(x2(m)-x1(m)) - x1(m)*(y2(m)-y1(m));for ii = 1:3if ((x1(m)-xobs(ii))^2 + (y1(m)-yobs(ii))^2) < robs(ii)^2 || ((x2(m)-xobs(ii))^2 + (y2(m)-yobs(ii))^2) < robs(ii)^2% disp('有点在圆内')cnt_line = cnt_line + 1;continue;else            d = abs(A*xobs(ii)+B*yobs(ii)+C) / sqrt(A^2+B^2);if d==0d1 = (xobs(ii)-x1(m))^2 + (yobs(ii)-y1(m))^2;d2 = (x2(m)-x1(m))^2 + (y2(m)-y1(m))^2;if d1 < d2cnt_line = cnt_line + 1;   % 该线段过圆心且穿过圆endelseif d < robs(ii)cos1 = (x2(m)-x1(m))*(xobs(ii)-x1(m)) + (y2(m)-y1(m))*(yobs(ii)-y1(m));cos2 = (x1(m)-x2(m))*(xobs(ii)-x2(m)) + (y1(m)-y2(m))*(yobs(ii)-y2(m));if cos1>0 && cos2>0cnt_line = cnt_line + 1;    % 该线段与圆交与两点endelsecontinue;endendendend%%%计算适应度if cnt_line > 0f(i)=0;       %路线穿过障碍物的个体适应度置零elsefor j=1:1:xn-1d(j)=sqrt((x(i,j+1)-x(i,j)).^2+(y(i,j+1)-y(i,j)).^2);     %该个体（即路线）的路径长度endf(i)=1.0/sum(d);       %取距离的倒数作为个体适应度endrecord_cnt(i,:) = cnt_line;endI = find(f ~= 0);sumf = sum(exp(f(I) ./ T)) + n - size(I, 1);f(I) = exp(f(I)./T) ./ sumf;fitval=f';
%     disp(['不满足条件的最小线段数为：',num2str(min(record_cnt, [], 1))])end

popinit

%====================================
%%输入参数：种群数量，染色体长度
%%输出参数：初始种群
%%说明：
%     种群中的个体由一系列点组成，该点的x，y坐标分开存放，
%     除了起点和终点，其余点随机生成并从小到大排序
%====================================
function [x,y]=popinit(popsize,chromlength)x=5.0*rand(popsize,chromlength);y=8.9*rand(popsize,chromlength);x(:,1)=0;  % 设置起点y(:,1)=0;for i=1:1:size(x,1) x(i,:)=sort(x(i,:));y(i,:)=sort(y(i,:));end x(:,chromlength)=1.5;  %设置终点y(:,chromlength)=8.9;end

mutation

%====================================
%%输入参数：父代种群，变异概率
%%输出参数：子代种群
%%说明：
%     随机替换，最后需要从小到大排序
%====================================
function [kidx, kidy]=mutation(x, y, p)[m, n] = size(x);kidx = x;kidy = y;for i = 1:1:mif(rand < p)point = round(rand*n);% 避免越界if point <= 1point = 2;endif point == npoint = n-1;end% 变异：随机数替换kidx(i,point) = round(rand*n);kidy(i,point) = round(rand*n);endendfor i = 1:1:mkidx(i,:) = sort(kidx(i,:));kidy(i,:) = sort(kidy(i,:));end 
end

fitness

%====================================
%%输入参数：种群——x,y横纵坐标
%%输出参数：种群中每个个体的适应度值
%%说明：
%     逐个计算种群中个体的适应度值，判断该个体所连成线路与圆形障碍物之间的关系，
%     将满足条件的路径的距离倒数作为适应度值
%====================================function fitval=fitness(x,y)%obstaclexobs=[1.5 4.0 1.2];yobs=[6.5 3.0 1.5];robs=[1.5 1.0 0.8];[n, xn] = size(x);for i=1:1:ncnt_line = 0;  %记录穿过障碍物的线段数%%拆分相邻的两个点，便于后续计算for m=1:1:xn-1x1(m)=x(i,m);y1(m)=y(i,m);endfor n=2:1:xnx2(n-1)=x(i,n);y2(n-1)=y(i,n);end%%判断线段与障碍物的关系for m = 1:size(x1,2)A = y2(m) - y1(m);B = x1(m) - x2(m);C = y1(m)*(x2(m)-x1(m)) - x1(m)*(y2(m)-y1(m));for ii = 1:3if ((x1(m)-xobs(ii))^2 + (y1(m)-yobs(ii))^2) < robs(ii)^2 || ((x2(m)-xobs(ii))^2 + (y2(m)-yobs(ii))^2) < robs(ii)^2% disp('有点在圆内')cnt_line = cnt_line + 1;continue;else            d = abs(A*xobs(ii)+B*yobs(ii)+C) / sqrt(A^2+B^2);if d==0d1 = (xobs(ii)-x1(m))^2 + (yobs(ii)-y1(m))^2;d2 = (x2(m)-x1(m))^2 + (y2(m)-y1(m))^2;if d1 < d2cnt_line = cnt_line + 1;   % 该线段过圆心且穿过圆endelseif d < robs(ii)cos1 = (x2(m)-x1(m))*(xobs(ii)-x1(m)) + (y2(m)-y1(m))*(yobs(ii)-y1(m));cos2 = (x1(m)-x2(m))*(xobs(ii)-x2(m)) + (y1(m)-y2(m))*(yobs(ii)-y2(m));if cos1>0 && cos2>0cnt_line = cnt_line + 1;    % 该线段与圆交与两点endelsecontinue;endendendend%%%计算适应度if cnt_line > 0f(i)=0;       %路线穿过障碍物的个体适应度置零elsefor j=1:1:xn-1d(j)=sqrt((x(i,j+1)-x(i,j)).^2+(y(i,j+1)-y(i,j)).^2);     %该个体（即路线）的路径长度endf(i)=1.0/sum(d);       %取距离的倒数作为个体适应度endrecord_cnt(i,:) = cnt_line;endfitval=f';
%     disp(['不满足条件的最小线段数为：',num2str(min(record_cnt, [], 1))])end

crossover

%====================================
%%输入参数：父代种群，交叉概率
%%输出参数：子代种群
%%说明：
%     单点交叉，最后需要从小到大排序
%====================================
function [kidx, kidy]=crossover(x, y, p)[m,n] = size(x);kidx = ones(size(x)); kidy = ones(size(y)); for i = 1:2:m-1if(rand < p)point = round(rand*n);kidx(i,:) = [x(i,1:point),x(i+1,point+1:n)];kidx(i+1,:) = [x(i+1,1:point),x(i,point+1:n)];kidy(i,:) = [y(i,1:point),y(i+1,point+1:n)];kidy(i+1,:) = [y(i+1,1:point),y(i,point+1:n)];elsekidx(i,:) = x(i,:);kidx(i+1,:) = x(i+1,:);kidy(i,:) = y(i,:);kidy(i+1,:) = y(i+1,:);endendfor i = 1:1:mkidx(i,:) = sort(kidx(i,:));kidy(i,:) = sort(kidy(i,:));end 
end

best

%====================================
%%输入参数：种群、其适应度
%%输出参数：种群中的最佳个体，及其适应度
%%说明：
%     选择最佳个体，便于后续分析
%====================================
function [bestx,besty,bestfit]=best(x,y,fitval)bestx = x(1,:);besty = y(1,:);bestfit = fitval(1);for i = 2:size(x,1)if fitval(i) > bestfitbestx = x(i,:);besty = y(i,:);bestfit=fitval(i);endend
end

运行效果
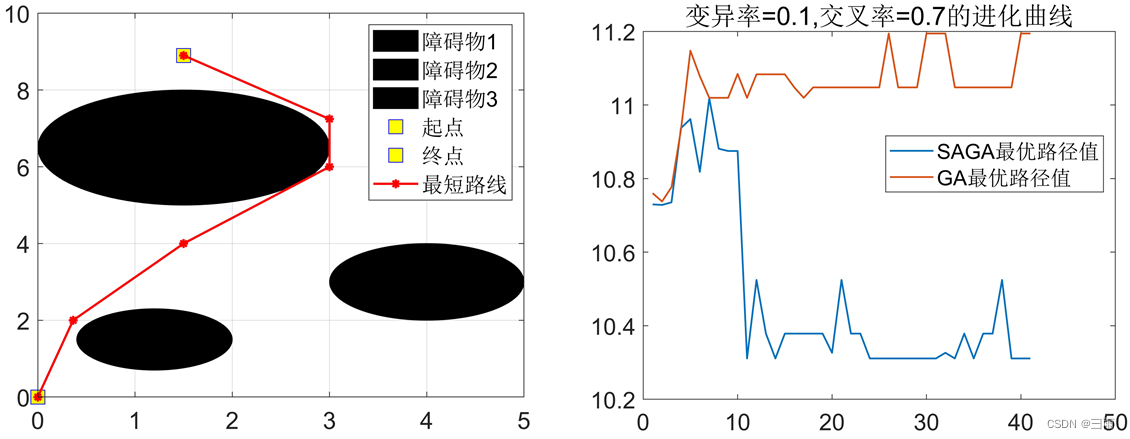
在这里插入图片描述

参考：
[1]https://www.bilibili.com/video/BV1XC4y1J7cN/?spm_id_from=333.337.search-card.all.click&vd_source=7a4fcf1e79c6c978598c4f5c8e5dddf0
[2]https://zhuanlan.zhihu.com/p/100337680
[3]https://zhuanlan.zhihu.com/p/136393730
[4]https://blog.csdn.net/weixin_44231148/article/details/112918109?spm=1001.2014.3001.5506
[5]https://blog.csdn.net/hba646333407/article/details/103251008
[6]https://blog.csdn.net/u011125673/article/details/97398874
[7]http://t.csdnimg.cn/nQsrf
[8]https://blog.csdn.net/KeepingMatlab/article/details/134624717
[9]https://zhuanlan.zhihu.com/p/266874840

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/219443.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

1.3 第一个C程序

1.3 第一个C程序

一、Dev-C的安装 下载地址&#xff1a;https://sourceforge.net/projects/orwelldevcpp/ 二、Dev-C简单的使用 2.1 首次打开配置 2.2 第一个程序的编辑、编译、运行 三、Hello Word程序讲解 3.1 程序框架 几乎所有的程序都需要这一段代码 3.2 输出 printf("Hello World…
阅读更多...
workflow系列教程(4)Parallel并联任务流

workflow系列教程(4)Parallel并联任务流

往期教程 如果觉得写的可以,请给一个点赞关注支持一下 观看之前请先看,往期的博客教程,否则这篇博客没办法看懂 workFlow c异步网络库编译教程与简介 C异步网络库workflow入门教程(1)HTTP任务 C异步网络库workflow系列教程(2)redis任务 workflow系列教程(3)Series串联任务流…
阅读更多...
AICore 带来了 Android 专属的 AI 能力，它要解决什么？采用什么架构思路？

AICore 带来了 Android 专属的 AI 能力，它要解决什么？采用什么架构思路？

前言 Google 最近发布的 Gemini 模型在全球引起了巨大反响&#xff0c;其在多模态领域的 Video demo 无比震撼。对于 Android 开发者而言&#xff0c;其中最振奋人心的消息莫过于 Gemini Nano 模型将内置到 Android 系统当中&#xff0c;并开放给开发者使用。 事实上&#xf…
阅读更多...
【产品经理】产品专业化提升路径

【产品经理】产品专业化提升路径

产品专业化就是上山寻路&#xff0c;梳理一套作为产品经理的工作方法。本文作者从设计方法、三基座、专业强化、优秀产品拆解、零代码这五个方面&#xff0c;对产品经理的产品专业化进行了总结归纳&#xff0c;一起来看一下吧。 产品专业化就是上山寻路&#xff0c;梳理一套作为…
阅读更多...
接口自动化测试框架【AIM】

接口自动化测试框架【AIM】

最近在做公司项目的自动化接口测试&#xff0c;在现有几个小框架的基础上&#xff0c;反复研究和实践&#xff0c;搭建了新的测试框架。利用业余时间&#xff0c;把框架总结了下来。 AIM框架介绍 AIM&#xff0c;是Automatic Interface Monitoring的简称&#xff0c;即自动化…
阅读更多...
c++ websocket 协议分析与实现

c++ websocket 协议分析与实现

前言 网上有很多第三方库&#xff0c;nopoll,uwebsockets,libwebsockets,都喜欢回调或太复杂&#xff0c;个人只需要在后端用&#xff0c;所以手动写个&#xff1b; 1:环境 ubuntu18 g(支持c11即可) 第三方库:jsoncpp,openssl 2:安装 jsoncpp 读取json 配置文件 用 自动安装 网…
阅读更多...
docker小白第五天

docker小白第五天

docker小白第五天 docker的私有库 有些涉密的信息代码不能放在阿里云的镜像仓库&#xff0c;因此需要构建一个个人内网专属的私有库&#xff0c;将镜像或者容器代码进行推送保存。 下载镜像docker registry 执行代码docker pull registry&#xff0c;用于搭建私服前的准备。…
阅读更多...
微信小程序---使用npm包安装Vant组件库

微信小程序---使用npm包安装Vant组件库

在小程序项目中&#xff0c;安装Vant 组件库主要分为如下3步: 注意&#xff1a;如果你的文件中不存在pakage.json&#xff0c;请初始化一下包管理器 npm init -y 1.通过 npm 安装(建议指定版本为1.3.3&#xff09; 通过npm npm i vant/weapp1.3.3 -S --production 通过y…
阅读更多...
EasyExcel 简单导入

EasyExcel 简单导入

前边写过使用easyexcel进行简单、多sheet页的导出。今天周日利用空闲写一下对应简单的导入。 重点&#xff1a;springboot、easyExcel、桥接模式&#xff1b; 说明&#xff1a;本次使用实体类student&#xff1a;属性看前边章节内容&#xff1b; 1、公共导入service public …
阅读更多...
gitee提交代码步骤介绍（含git环境搭建）

gitee提交代码步骤介绍（含git环境搭建）

1、gitee官网地址 https://gitee.com; 2、Windows中安装git环境 参考博客&#xff1a;《Windows中安装Git软件和TortoiseGit软件》&#xff1b; 3、设置用户名和密码 这里的用户名和密码就是登录gitee网站的用户名和密码如果设置错误&#xff0c;可以在Windows系统的“凭据管理…
阅读更多...
C#面试题

C#面试题

目录 基本概念 装箱和拆箱 1、装箱拆箱的“箱”是什么&#xff0c;“箱”存放在哪里&#xff1f; 2、装箱快还是拆箱快&#xff1f; 3、装箱和拆箱有什么性能影响&#xff1f; 值类型和引用类型分别是哪些 访问权限修饰符 委托(delegate) 什么是委托链 委托链用途 事件…
阅读更多...
【C语言】实战项目——通讯录

【C语言】实战项目——通讯录

引言 学会创建一个通讯录&#xff0c;对过往知识进行加深和巩固。 文章很长&#xff0c;要耐心学完哦&#xff01; ✨ 猪巴戒&#xff1a;个人主页✨ 所属专栏&#xff1a;《C语言进阶》 &#x1f388;跟着猪巴戒&#xff0c;一起学习C语言&#x1f388; 目录 引言 实战 建…
阅读更多...
VLAN间的通讯---三层交换

VLAN间的通讯---三层交换

一.三层交换 1.概念 使用三层交换技术实现VLAN间通信 三层交换二层交换 三层转发 2.基于CEF的MLS CEF是一种基于拓补转发的模型 转发信息库&#xff08;FIB&#xff09;临接关系表 转发信息库&#xff08;FIB&#xff09;可以理解为路由表 邻接关系表可以理解为MAC地址表…
阅读更多...
Linux驱动（中断、异步通知）：红外对射，并在Qt StatusBus使用指示灯进行显示

Linux驱动（中断、异步通知）：红外对射，并在Qt StatusBus使用指示灯进行显示

本文工作&#xff1a; 1、Linux驱动与应用程序编写&#xff1a;使用了设备树、中断、异步通知知识点&#xff0c;实现了红外对射状态的异步信息提醒。 2、QT程序编写&#xff1a;自定义了一个“文本指示灯”类&#xff0c;并放置在QMainWidget的StatusBus中。 3、C与C混合编程与…
阅读更多...
【华为数据之道学习笔记】5-4 数据入湖方式

【华为数据之道学习笔记】5-4 数据入湖方式

数据入湖遵循华为信息架构&#xff0c;以逻辑数据实体为粒度入湖&#xff0c;逻辑数据实体在首次入湖时应该考虑信息的完整性。原则上&#xff0c;一个逻辑数据实体的所有属性应该一次性进湖&#xff0c;避免一个逻辑实体多次入湖&#xff0c;增加入湖工作量。 数据入湖的方式…
阅读更多...
Android Studio好用的插件推荐

Android Studio好用的插件推荐

目录 一、插件推荐 二、如何下载 1.点击File—>Settings ​2.点击Plugins然后进行搜索下载 三、Android Studio 模板 一、插件推荐 这个插件可以为您自动生成Parcelable代码。Parcelable是一种用于在Android组件之间传递自定义对象的机制&#xff0c;但手动编写Parcela…
阅读更多...
RabbitMQ搭建集群环境、配置镜像集群、负载均衡

RabbitMQ搭建集群环境、配置镜像集群、负载均衡

RabbitMQ集群搭建 Linux安装RabbitMQ下载安装基本操作命令开启管理界面及配置 RabbitMQ集群搭建确定rabbitmq安装目录启动第一个节点启动第二个节点停止命令创建集群查看集群集群管理 RabbitMQ镜像集群配置启用HA策略创建一个镜像队列测试镜像队列 负载均衡-HAProxy安装HAProxy…
阅读更多...
从计算机底层深入Golang高并发

从计算机底层深入Golang高并发

从计算机底层深入Golang高并发 1.源码流程架构图 2.源码解读 runtime/proc.go下的newpro() func newproc(fn *funcval) {//计算额外参数的地址argpgp : getg()pc : getcallerpc()//s1使用systemstack调用newproc1 systemstack(func() {newg : newproc1(fn, gp, pc)_p_ : getg…
阅读更多...
代码随想录二刷 ｜ 二叉树 ｜ 112. 路径总和

代码随想录二刷 ｜ 二叉树 ｜ 112. 路径总和

代码随想录二刷 &#xff5c; 二叉树 &#xff5c; 112. 路径总和 题目描述解题思路递归迭代 代码实现递归迭代 题目描述 112.路径总和 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径&#xff0c;这条路径上所有节…
阅读更多...
leetcode-138-随机链表的复制（Java实现）

leetcode-138-随机链表的复制（Java实现）

题目&#xff1a; 给你一个长度为 n 的链表&#xff0c;每个节点包含一个额外增加的随机指针 random &#xff0c;该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成&#xff0c;其中每个新节点的值都设为其对应的原节点…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023