题意理解:
求一个集合的子集:该集合有重复元素。
集合[1,2,2]
[]、[1]、[2]、[2]、[12]、[12]、[22]、[122]
子集:[]、[1]、[2]、[12]、[22]、[122]——由于元素有重复需要对子集进行去重操作。
所以此题的难点在于:子集去重
解题思路:
首先明确,组合类、子集类、排列类都可以使用回溯的方法来做。
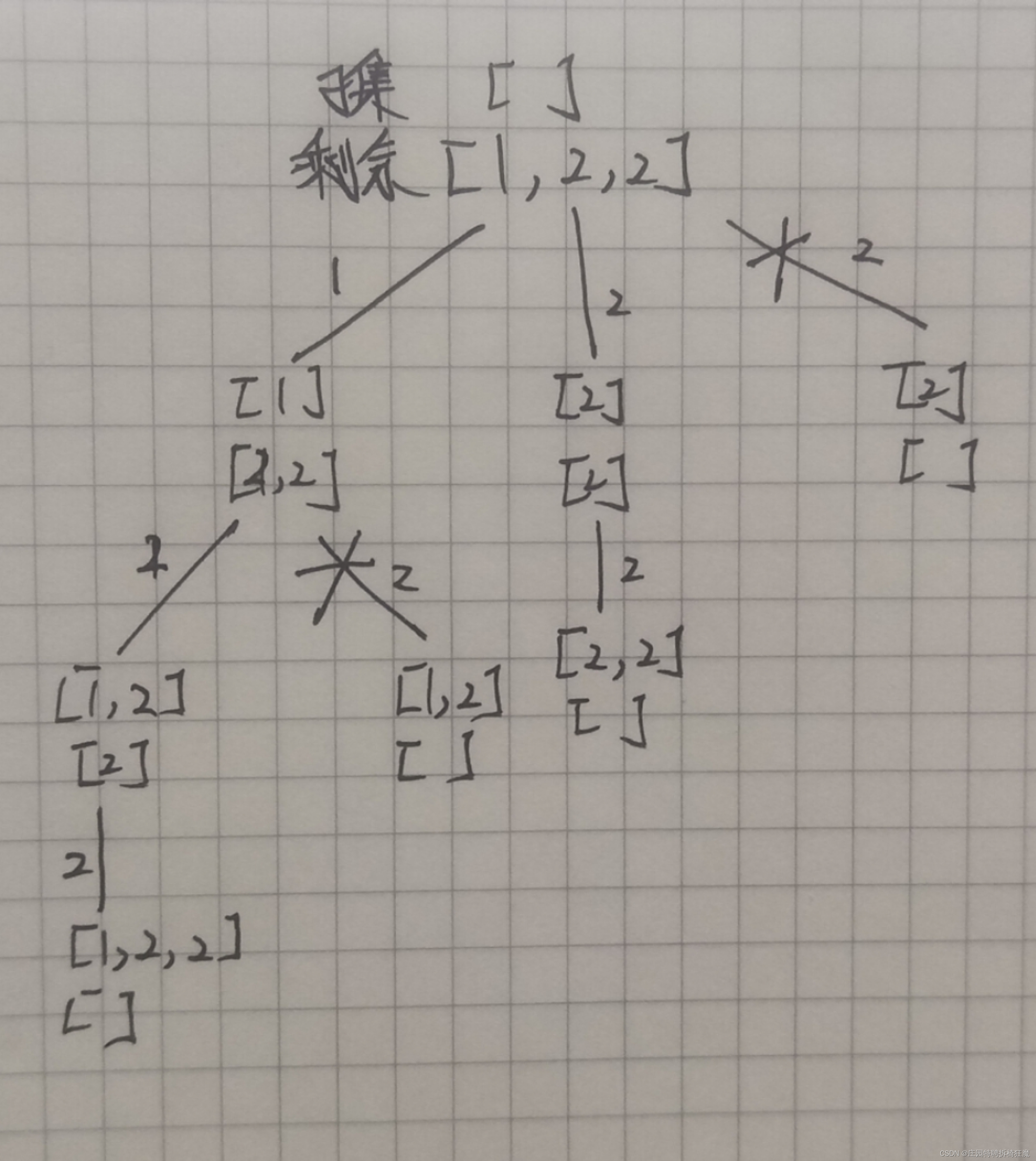
所以,要将问题的解决抽象成一棵树。
如图所见,所有子集在每个节点处收集。
特别的,有两个地方发生了剪枝。所以我们何时进行剪枝操作呢?——发生重复子集时,剪枝。
这里引入《代码随想录》中所说的:树层去重的逻辑。
什么是树层去重:
当前层树枝取到重复数字时,则可能回触发重复结果的产生。
如何判断是否取得相同值呢?可以使用nums[i]==nums[i-1]来进行判断。
但是:如[2,2]子集,满足nums[i]==nums[i-1],但是不是同层。
如何判断是同一层呢?使用used[]数组来维护一个当前集合是否访问过的状态。
若used[i-1]=0且nums[i]==nums[i-1],则说明,同层有重复值。详细可以在树结构上理解。
used[i-1]=0且nums[i]==nums[i-1],就是当前分支新的探索范围是从当前值往后,上一个值已经作为一个分支处理过了,又因为nums[i]==nums[i-1],这就会导致重复的子集分支,故此种情况需要剪枝。
used[i-1]=1且nums[i]==nums[i-1],就是当前分支新的探索范围是从当前值往后,且当前分支在该子集内,虽然nums[i]==nums[i-1],但是他们属于同一个树枝的不同层。所以不会导致同层树枝取相同数值导致重复问题,故不需要剪枝。
1.暴力回溯+剪枝优化
解决子集问题,可以使用回溯算法,将解题思路抽象成一棵树。
前提准确:nums数组应提前处理为有序数组,以便后续操作。
明确回溯算法的三个步骤:结果在每一个节点收集,每进入一次递归函数,就相当于达到一个节点,所以在方法已进入的地方收集结果。
确定返回值和参数列表,一般是void
确定终止条件
确定单层逻辑。
List<List<Integer>> result=new ArrayList<>();LinkedList<Integer> path=new LinkedList<>();boolean[] used=null;public List<List<Integer>> subsetsWithDup(int[] nums) {used=new boolean[nums.length];//默认值falseArrays.sort(nums);backtracking(nums,0);return result;}public void backtracking(int[] nums,int satrtIndex){result.add(new ArrayList<>(path));if(satrtIndex>=nums.length) return;//其实可以省略,satrtIndex>=nums.length时,不会进下面的循环,方法直接结束//但是写着方便理解for(int i=satrtIndex;i<nums.length;i++){//数层剪枝if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;path.add(nums[i]);used[i]=true;//递归backtracking(nums,i+1);//回溯操作path.removeLast();used[i]=false;}}2.分析
时间复杂度:O(
)
空间复杂度:O(n)