目录
一.processon图形的使用场景介绍
二.流程图绘画
三.泳道图的绘画
1.绘制门诊流程图绘制门诊泳道图
2. 绘制住院泳道图编辑
3.绘制药库采购入库流程图
4.绘制OA会议泳道图
四.Axure自定义元件
1.Axure载入元件库
一.processon图形的使用场景介绍
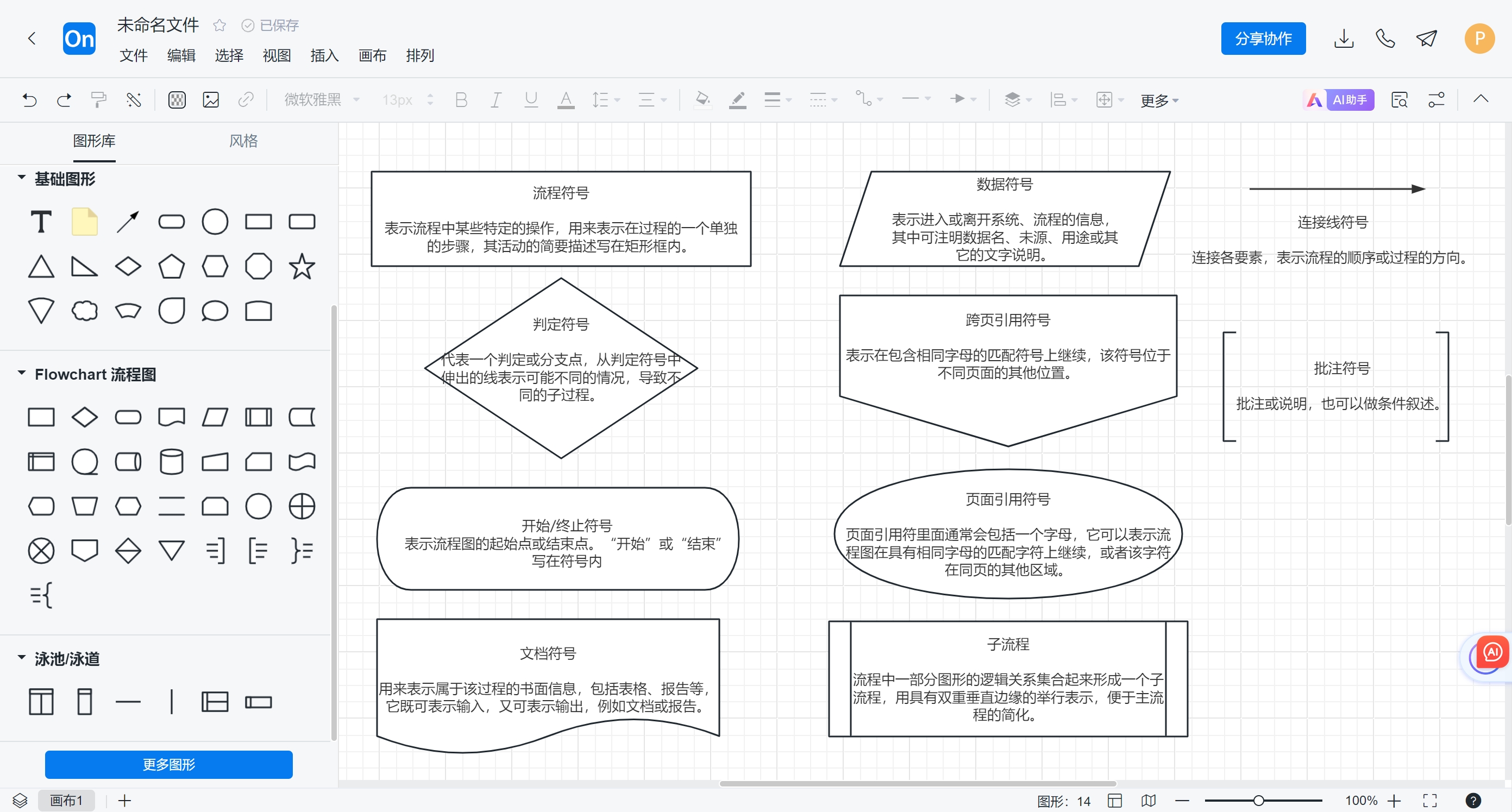
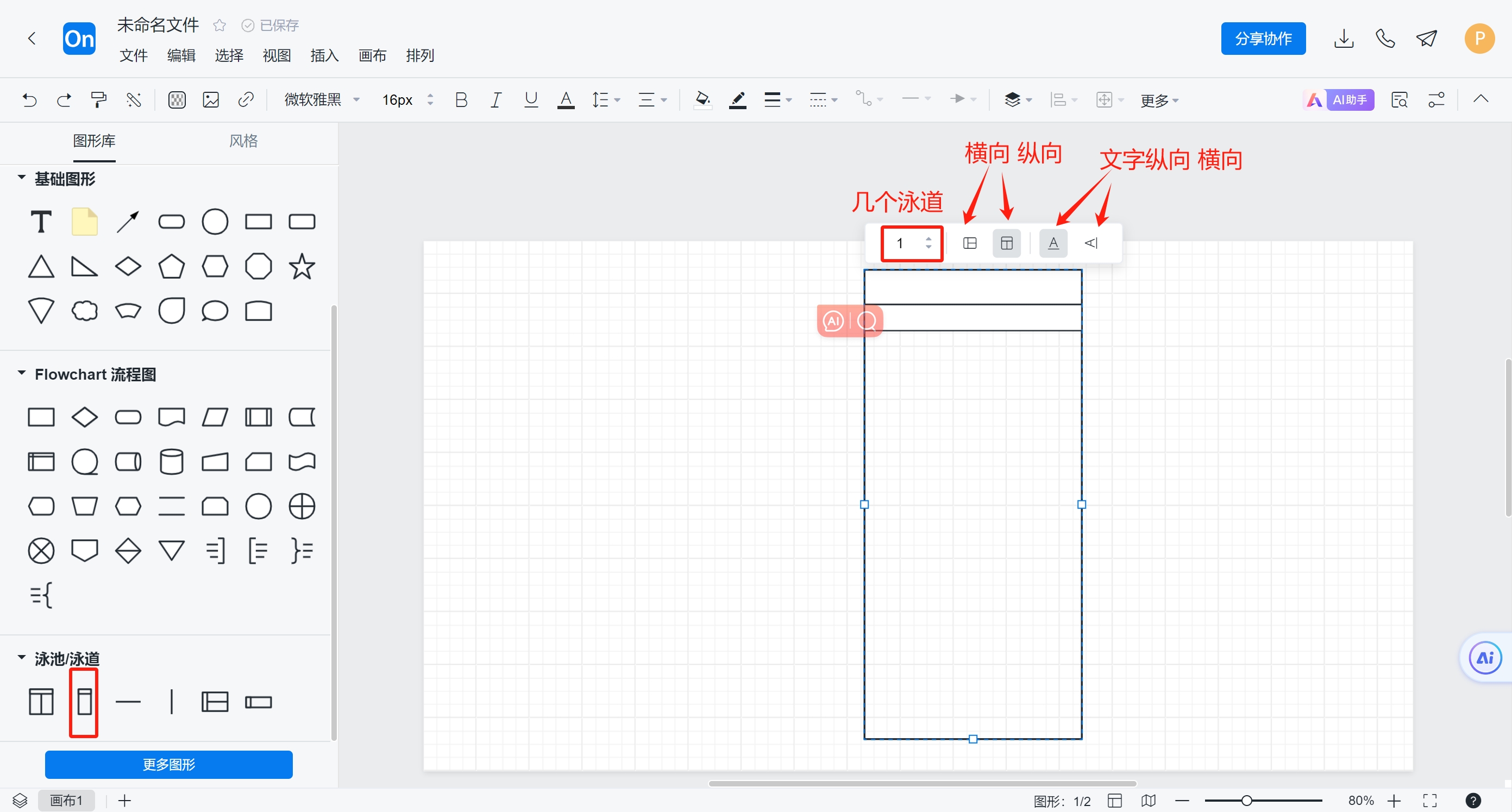
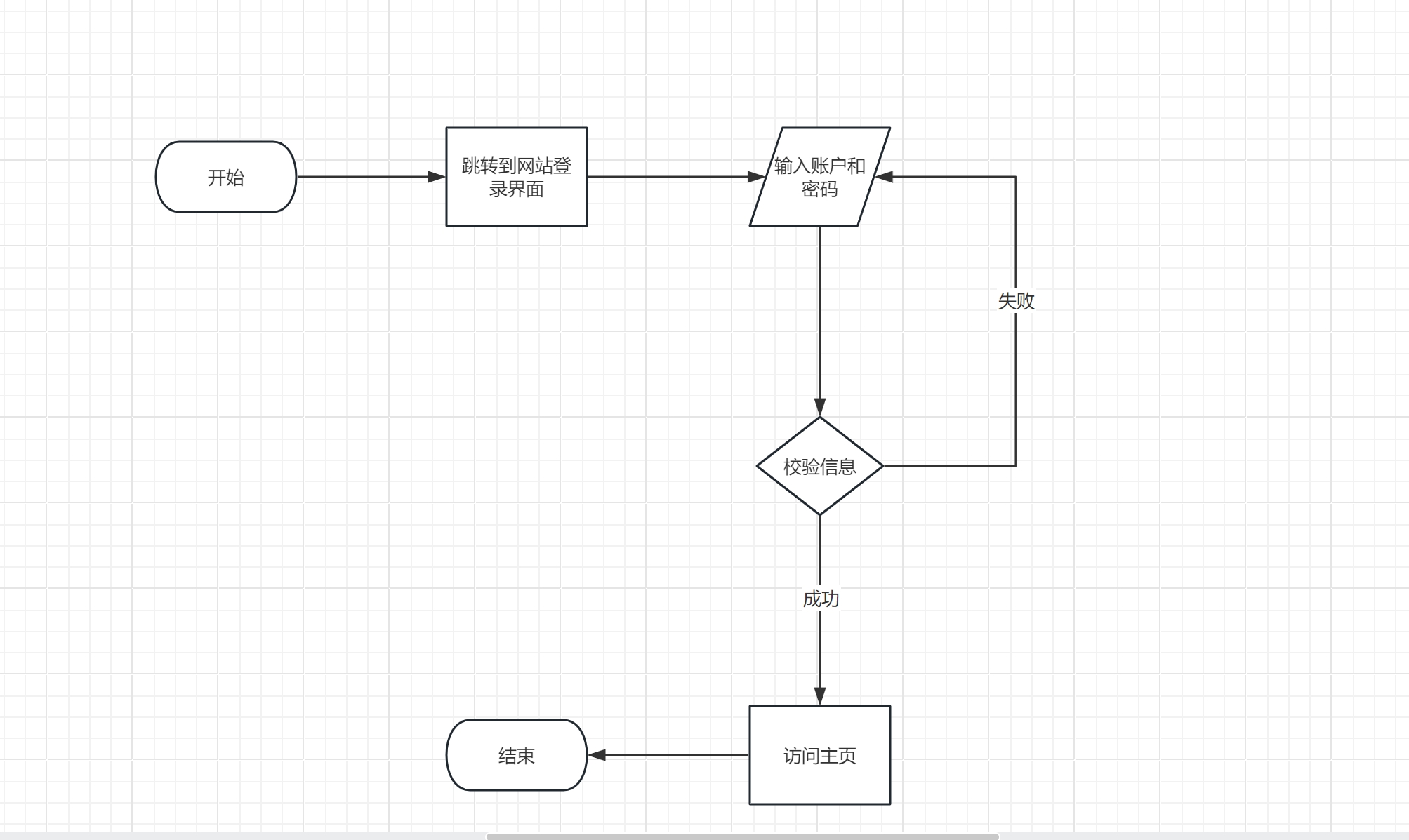
二.流程图绘画
示例:登录界面流程图案例
三.泳道图的绘画
1.绘制门诊流程图绘制门诊泳道图

2. 绘制住院泳道图
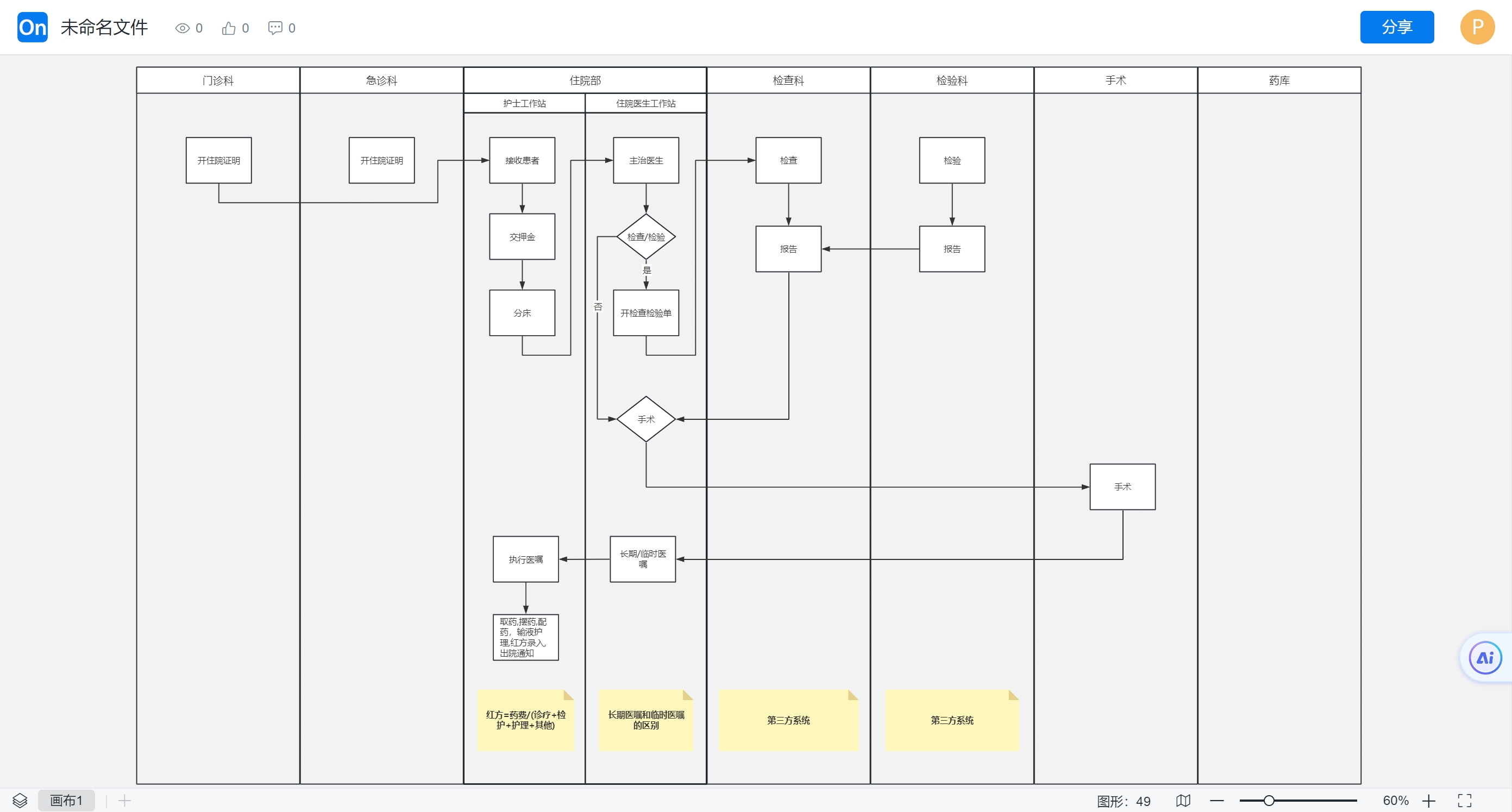
3.绘制药库采购入库泳道图

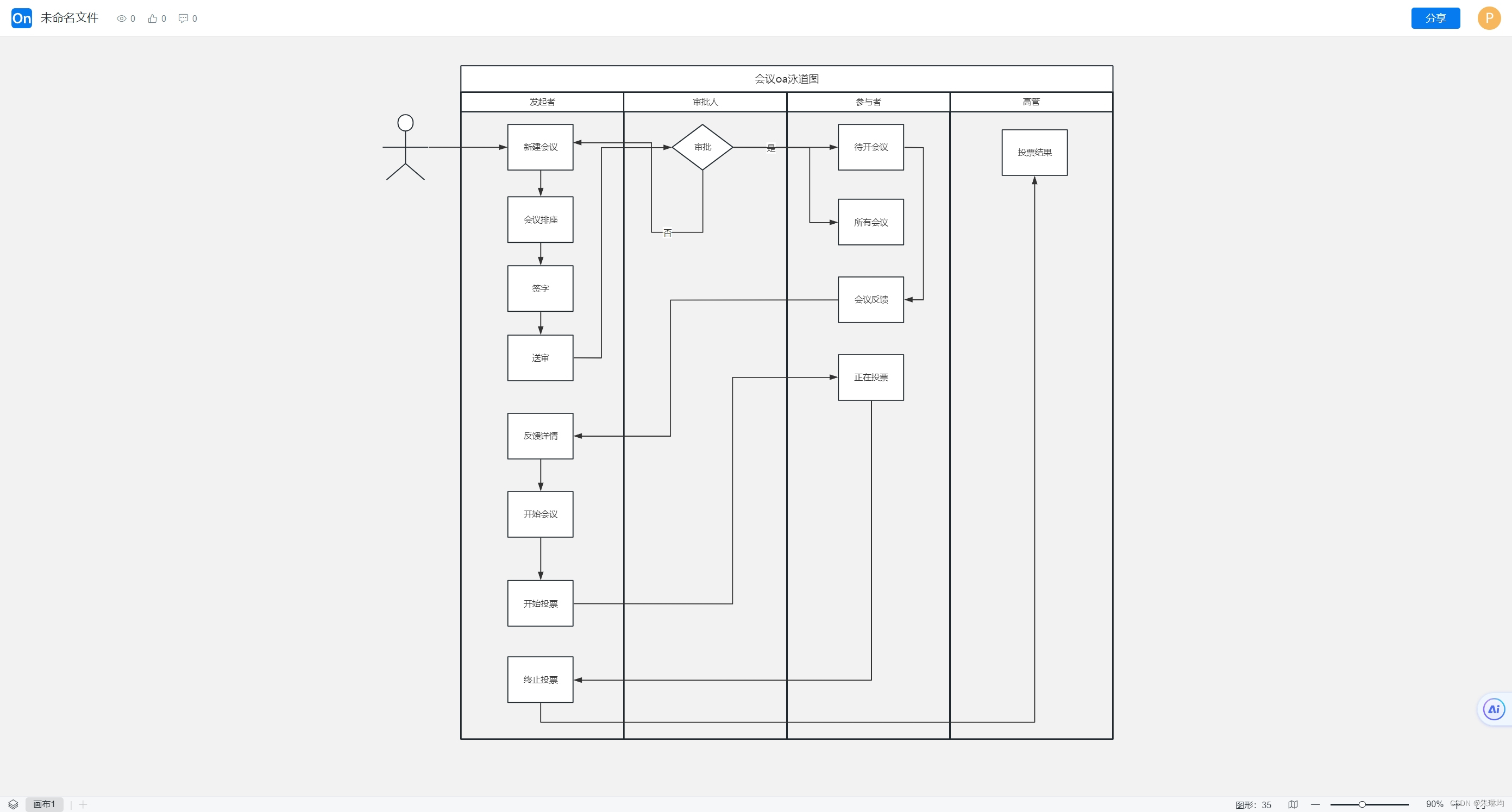
4.绘制OA会议泳道图
四.Axure自定义元件
1.Axure载入元件库
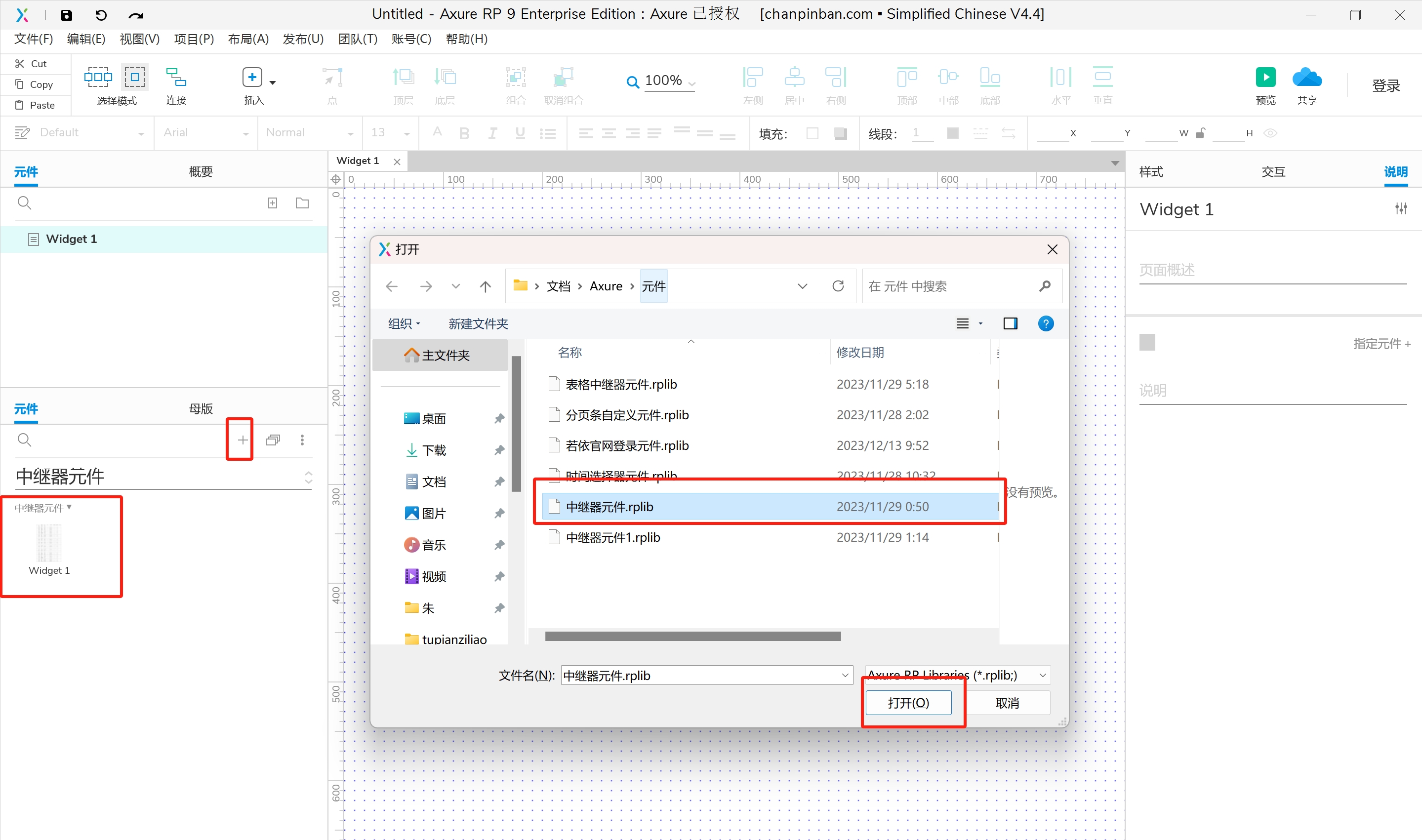
打开Axure左上脚文件->第二个选项自定义元件库->Ctrl+s保存,命名->重新打开Axure在自定义元件库就可以看到你命名绘画好的自定义元件库了 或者
在Ctrl+s保存后,点击左侧一个加号图标,选择保存路径就可以看到你命名绘画好的自定义元件库了

![[Kubernetes]3. k8s集群Service详解](https://img-blog.csdnimg.cn/direct/0f90740aef3c4283b109aa8ba52519fe.png)