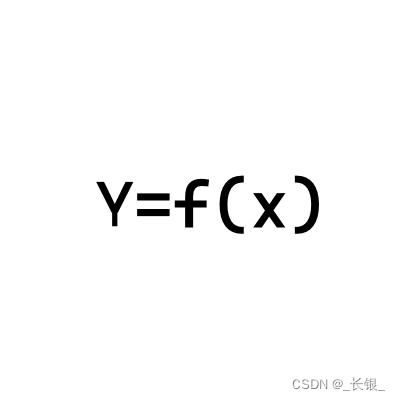SVM
- 支持向量
- 线性可分
- 最大间隔超平面
- 最大间隔超平面的推导
- 支持向量
- 分类间隔的推导
- 最优化问题
- 对偶问题
- 拉格朗日乘子法
- 强对偶性
- SVM 优化
- 软间隔
- 解决问题
- 优化目标及求解
- 核函数
- 线性不可分
- 核函数的作用
- 常见核函数
- SVM 算法优缺点
支持向量机(Support Vector Machine,SVM)是一种常用的监督学习算法,主要用于分类和回归任务。它的核心思想是找到一个最优的超平面或者曲面,将不同类别的样本点分开。
在二分类问题中,SVM 试图找到一个超平面来将两个类别的样本点分隔开,并使得两个类别距离超平面的最小间隔最大化。这个超平面被称为最大间隔超平面。对于非线性可分的情况,SVM 可以通过使用核函数将输入空间映射到高维特征空间,从而使数据在新的特征空间中线性可分。
训练 SVM 模型的过程包括以下步骤:
- 收集和准备训练数据集,确保数据集中的标签已知。
- 选择合适的核函数,并确定相应的参数。
- 构建目标函数,即最大化间隔的优化问题。
- 使用优化算法求解目标函数,找到最优的超平面或者曲面。
- 根据训练好的模型进行预测和分类。
支持向量
线性可分
通俗的讲:在二维空间中,如果两类点能够被一条直线完全分开,那么这两类点就是线性可分的。
严格的讲: D 0 D_0 D0 和 D 1 D_1 D1 是 n n n 维欧式空间中的两个点集,如果存在 n n n 维向量 w w w 和实数 b b b,使得所有属于 D 0 D_0 D0 点 x i x_i xi 都有 w x i + b > 0 wx_i + b > 0 wxi+b>0,而所有属于 D 1 D_1 D1 的点 x j x_j xj 都有 w x j + b < 0 wx_j + b < 0 wxj+b<0,则称 D 0 D_0 D0 和 D 1 D_1 D1 线性可分。

我们从线性可分的二分类问题入手,如下图所示:

上述图中,红点和蓝点分别表示两个不同的类别,数据显然是线性可分的,但是能够将两类数据分开的直线也显然不止一条。中间那条黑色实线为分界线,我们称之为决策面,一个决策面对应一个线性分类器。从分类结果上看,分类器 A 和分类器 B 的分类效果是相同的,都能把两个类别完全分开。
实际上,分类器 A 和分类器 B 的分类性能是有差距的,如下图所示:

在决策面不变的情况下,添加了一个红点数据。可以看到,分类器 A 依然能够很好的对其进行分类,而分类器 B 则出现了分类错误,显然分类器 A 的决策面更加稳健。
最大间隔超平面
在决策面不变且不会错分样本的情况下,移动决策面,可以在原决策面两侧分别找到一个极限位置,越过该位置就会导致错分,如上图中的虚线所示。虚线的位置由距离原决策面最近的样本点决定,两条虚线之间的垂直距离就是决策面的分类间隔。
显然,每一个能把两类数据正确分开的方向都有一个最优决策面,这些最优决策面都有各自的分类间隔,其中具有最大间隔的决策面就是 SVM 算法要寻找的最优解。最优解对应的两条虚线穿过的样本点,就是 SVM 中的支持样本点,称之为支持向量。
从二维扩展到多维空间时,能将 D 0 D_0 D0 和 D 1 D_1 D1 完全分开的 w x + b = 0 wx + b = 0 wx+b=0 就成了一个超平面。为了使这个超平面更具鲁棒性,我们会寻找出一个最佳超平面(即以最大间隔把两类样本分开的超平面),也称之为最大间隔超平面。
最大间隔超平面的推导
我们知道二维空间中的直线方程可写成如下:
y = a x + b y = ax + b y=ax+b
我们做个小改动,将 x x x 轴变成 x 1 x_1 x1,将 y y y 轴变成 x 2 x_2 x2,则有:
x 2 = a x 1 + b ⟹ a x 1 − x 2 + b = 0 x_2 = ax_1 + b \implies ax_1 - x_2 + b = 0 x2=ax1+b⟹ax1−x2+b=0
将上述公式向量化,得:
[ a − 1 ] [ x 1 x 2 ] + b = 0 ⟹ w T x + b = 0 \begin{bmatrix}a & -1\end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix}+ b = 0 \implies w^Tx + b = 0 [a−1][x1x2]+b=0⟹wTx+b=0
将上述公式从二维空间推广到 n n n 维空间,就变成了超平面方程(一个超平面在二维空间中的实例就是一条直线)。
因此,超平面可以用下式表示:
w T x + b = 0 w^Tx + b = 0 wTx+b=0
其中, w = [ w 1 , w 2 , . . . , w n ] T w=[w_1, w_2, ..., w_n]^T w=[w1,w2,...,wn]T, x = [ x 1 , x 2 , . . . , x n ] T x=[x_1, x_2, ..., x_n]^T x=[x1,x2,...,xn]T。
支持向量

距离超平面最近的样本点,就叫做支持向量。
分类间隔的推导
在二维空间中,点 ( x , y ) (x, y) (x,y) 到直线 A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0 的距离公式可以写成如下:
d = ∣ A x + B y + C ∣ A 2 + B 2 d = \frac{|Ax+By+C|}{\sqrt {A^2 + B^2}} d=A2+B2∣Ax+By+C∣
将直线方程扩展到 n n n 维空间,点 x = ( x 1 , x 2 , . . . , x n ) x=(x_1, x_2, ..., x_n) x=(x1,x2,...,xn) 到超平面 w T x + b = 0 w^Tx + b = 0 wTx+b=0 的距离公式可以写成如下:
d = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ d = \frac{|w^Tx + b|}{||w||} d=∣∣w∣∣∣wTx+b∣
其中, ∣ ∣ w ∣ ∣ = w 1 2 + w 2 2 + ⋅ ⋅ ⋅ + w n 2 ||w||=\sqrt {w_1^2 + w_2^2 + ··· + w_n^2} ∣∣w∣∣=w12+w22+⋅⋅⋅+wn2。
上式中的 d d d 就是分类间隔,分类间隔越大,我们就认为这个超平面的分类效果越好。此时,求解超平面的问题就转化成了求解分类间隔最大化的问题。
最优化问题
求解最佳超平面(最大间隔超平面)的过程,就叫做最优化。一个最优化问题通常考虑两个基本要素,目标函数与优化对象。在求解最佳超平面的过程中,分类间隔就是目标函数,超平面就是优化对象。我们需要对分类间隔与超平面进行数学建模。
超平面方程在上文中已推导得出,即为 w T x + b = 0 w^Tx + b = 0 wTx+b=0。其中 w w w 是超平面的法向量, b b b 是截距。假设有一个超平面能够将正例和负例完全分开,正例的标签为 1,负例的标签为 -1,那么我们的目标就是要找到最优的 w w w 和 b b b,使得所有正例点满足 w T x + b > = 1 w^Tx + b >= 1 wTx+b>=1,所有负例点满足 w T x + b < = − 1 w^Tx + b <= -1 wTx+b<=−1,并且最大化间隔(即正例点和负例点到超平面的距离之和)。
分类间隔方程在上文中也已推导得出,即为 d = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ d = \frac{|w^Tx + b|}{||w||} d=∣∣w∣∣∣wTx+b∣,这个就是目标函数。根据支持向量的定义我们知道,支持向量到超平面的距离为 d d d,其他样本点到超平面的距离大于 d d d。

于是,我们可以得出:
{ w T x + b ∣ ∣ w ∣ ∣ ≥ d y = 1 w T x + b ∣ ∣ w ∣ ∣ ≤ − d y = − 1 \left\{\begin{matrix}\frac{w^Tx + b}{||w||} \ge d & y = 1 \\ \frac{w^Tx + b}{||w||} \leq -d & y = -1\end{matrix}\right. {∣∣w∣∣wTx+b≥d∣∣w∣∣wTx+b≤−dy=1y=−1
两边同时除以 d d d,得到:
{ w T x + b ∣ ∣ w ∣ ∣ d ≥ 1 y = 1 w T x + b ∣ ∣ w ∣ ∣ d ≤ − 1 y = − 1 \left\{\begin{matrix}\frac{w^Tx + b}{||w||d} \ge 1 & y = 1 \\ \frac{w^Tx + b}{||w||d} \leq -1 & y = -1\end{matrix}\right. {∣∣w∣∣dwTx+b≥1∣∣w∣∣dwTx+b≤−1y=1y=−1
由于 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 和 d d d 都是标量,都为正数,因此我们可以令 ∣ ∣ w ∣ ∣ d ||w||d ∣∣w∣∣d 为 1 1 1(之所以令它为 1 1 1,是为了方便后续的推导和优化,且这个做法对目标函数的优化并无影响),得到:
{ w T x + b ≥ 1 y = 1 w T x + b ≤ − 1 y = − 1 \left\{\begin{matrix}w^Tx + b \ge 1 & y = 1 \\ w^Tx + b \leq -1 & y = -1\end{matrix}\right. {wTx+b≥1wTx+b≤−1y=1y=−1
将两个方程合并(两边同乘以 y y y),得到:
y ( w T x + b ) ≥ 1 y(w^Tx + b) \ge 1 y(wTx+b)≥1
至此,我们可以得到超平面两侧的经过支持向量且与超平面平行的平面方程,如下图所示:

每个支持向量到超平面的距离可以写成如下:
d = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ d = \frac{|w^Tx + b|}{||w||} d=∣∣w∣∣∣wTx+b∣
由上述 y ( w T x + b ) ≥ 1 > 0 y(w^Tx + b) \ge 1 > 0 y(wTx+b)≥1>0,可以得到 y ( w T x + b ) = ∣ w T x + b ∣ y(w^Tx + b) = |w^Tx + b| y(wTx+b)=∣wTx+b∣, y = ± 1 y = \pm 1 y=±1,进而得到:
d = y ( w T x + b ) ∣ ∣ w ∣ ∣ d = \frac{y(w^Tx + b)}{||w||} d=∣∣w∣∣y(wTx+b)
我们可以最大化这个距离:
m a x 2 ∗ y ( w T x + b ) ∣ ∣ w ∣ ∣ max \ 2*\frac{y(w^Tx + b)}{||w||} max 2∗∣∣w∣∣y(wTx+b)
这里乘上 2 2 2 是为了方便后续的推导,对目标函数没有影响。支持向量样本点有 y ( w T x + b ) = ∣ w T x + b ∣ = 1 y(w^Tx + b) = |w^Tx + b| = 1 y(wTx+b)=∣wTx+b∣=1,因此得到最大化距离:
m a x 2 ∣ ∣ w ∣ ∣ max \ \frac{2}{||w||} max ∣∣w∣∣2
将求解 d d d 的最大化问题转化为最小化问题,之所以这样做是为了方便对目标函数进行求导,不影响求解最优化问题,上述式子等效于下式:
m i n 1 2 ∣ ∣ w ∣ ∣ min \ \frac{1}{2}||w|| min 21∣∣w∣∣
去除 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 的根号,便于后续计算,得到:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 min \ \frac{1}{2}||w||^2 min 21∣∣w∣∣2
将目标函数与约束条件放在一起进行描述,得到最优化模型:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 i = 1 , 2 , . . . , n min \ \frac{1}{2}||w||^2 \ \ s.t. \ \ y_i(w^Tx_i + b) \ge 1 \ \ i = 1, 2, ..., n min 21∣∣w∣∣2 s.t. yi(wTxi+b)≥1 i=1,2,...,n
上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型。
对偶问题
拉格朗日乘子法
如果集合中任意两个元素连线上的点也在集合中,那么这个集合就是凸集。
假设 f ( x ) f(x) f(x) 是定义在区间 L L L 上的函数,若对任意两点 x 1 , x 2 x_1, x_2 x1,x2 和任意的实数 λ ∈ ( 0 , 1 ) \lambda \in (0, 1) λ∈(0,1),总有 f ( λ x 1 + ( 1 − λ ) x 2 ) ≤ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) f(\lambda x_1 + (1 - \lambda)x_2) \leq \lambda f(x_1) + (1 - \lambda)f(x_2) f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2),则称 f ( x ) f(x) f(x) 为 L L L 上的凸函数。
通常,我们求解的最优化问题有如下几类:
-
无约束的优化问题,可以写成如下:
m i n f ( x 1 , x 2 , . . . , x n ) min \ f(x_1, x_2, ..., x_n) min f(x1,x2,...,xn)
对于此类问题,最常使用的方法便是费马定理,即求导,令导数为零,求出极值点。如果是凸函数,则能保证求出来的解是最优解。 -
有等式约束的优化问题,可以写成如下:
m i n f ( x 1 , x 2 , . . . , x n ) s . t . h i ( x 1 , x 2 , . . . , x n ) = 0 i = 1 , 2 , . . . , m min \ f(x_1, x_2, ..., x_n) \\ s.t. \ \ h_i(x_1, x_2, ..., x_n) = 0 \ \ i = 1, 2, ..., m min f(x1,x2,...,xn)s.t. hi(x1,x2,...,xn)=0 i=1,2,...,m
对于此类问题,最常使用的方法便是拉格朗日乘子法(Lagrange Multiplier),即用一个系数将等式约束与目标函数写在一起,形如 L ( x , λ ) = f ( x ) + ∑ i = 1 m λ i h i ( x ) L(x, \lambda) = f(x) + \displaystyle\sum_{i=1}^{m}\lambda _ih_i(x) L(x,λ)=f(x)+i=1∑mλihi(x), L ( x , λ ) L(x, \lambda) L(x,λ) 称为拉格朗日函数,系数 λ \lambda λ 称为拉格朗日乘子。对拉格朗日函数中的各变量进行求导,令其为零,可求得候选值集合,最后通过验证求得最优值。
利用必要条件找到可能的极值点,判断是否为极值点,需要根据问题本身的具体情况进行检验,式子如下:
{ ∂ L ∂ x i = 0 i = 1 , 2 , . . . , n ∂ L ∂ λ i = 0 i = 1 , 2 , . . . , m \left\{\begin{matrix}\frac{\partial L}{\partial x_i} = 0 & i = 1, 2, ..., n\\ \frac{\partial L}{\partial \lambda _i} = 0 & i = 1, 2, ..., m \end{matrix}\right. {∂xi∂L=0∂λi∂L=0i=1,2,...,ni=1,2,...,m
上述方程组称为等式约束的极值必要条件。等式约束下的拉格朗日乘子法引入了 m m m 个拉个朗日乘子,我们将 x i x_i xi 与 λ i \lambda _i λi 都视作优化变量,因此共有 ( n + m ) (n + m) (n+m) 个优化变量。 -
有不等式约束的优化问题,可以写成如下:
m i n f ( x 1 , x 2 , . . . , x n ) s . t . g i ( x 1 , x 2 , . . . , x n ) ≤ 0 i = 1 , 2 , . . . , m min \ f(x_1, x_2, ..., x_n) \\s.t. \ \ g_i(x_1, x_2, ..., x_n) \leq 0 \ \ i = 1, 2, ..., m min f(x1,x2,...,xn)s.t. gi(x1,x2,...,xn)≤0 i=1,2,...,m
对于此类问题,最常使用的方法便是 KKT 条件法。同样地,用系数将所有的等式、不等式约束与目标函数写在一起,写在一起的函数也称为拉格朗日函数,系数也叫拉格朗日乘子。
本文中的优化问题属于有不等式约束的优化,针对这种情况,主要思想是通过引入松弛变量将不等式约束转化为等式约束。

我们的最优化模型如下:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 s . t . g i ( w ) = 1 − y i ( w T x i + b ) ≤ 0 i = 1 , 2 , . . . , n min \ \frac{1}{2}||w||^2 \\ s.t. \ \ g_i(w) = 1 - y_i(w^Tx_i + b) \leq 0 \ \ i = 1, 2, ..., n min 21∣∣w∣∣2s.t. gi(w)=1−yi(wTxi+b)≤0 i=1,2,...,n
引入松弛变量 a i 2 a_i^2 ai2,得到 h i ( w , a i ) = g i ( w ) + a i 2 = 0 h_i(w, a_i) = g_i(w) + a_i^2 = 0 hi(w,ai)=gi(w)+ai2=0。这里加平方主要是为了不再引入新的约束条件,如果引入的松弛变量为 a i a_i ai,那我们必须要保证 a i ≥ 0 a_i \ge 0 ai≥0,才能使得 h i ( w , a i ) = 0 h_i(w, a_i) = 0 hi(w,ai)=0。
由此,我们将不等式约束转化为了等式约束,并得到拉格朗日函数:
L ( w , λ , a ) = f ( w ) + ∑ i = 1 n λ i h i ( w ) = f ( w ) + ∑ i = 1 n λ i [ g i ( w ) + a i 2 ] λ i ≥ 0 L(w, \lambda , a) = f(w) + \displaystyle\sum_{i=1}^{n}\lambda _ih_i(w) = f(w) + \displaystyle\sum_{i=1}^{n}\lambda _i[g_i(w) + a_i^2] \ \ \ \ \lambda _i \ge 0 L(w,λ,a)=f(w)+i=1∑nλihi(w)=f(w)+i=1∑nλi[gi(w)+ai2] λi≥0
根据等式约束优化问题的极值必要条件,联立方程:
{ ∂ L ∂ w i = ∂ f ∂ w i + ∑ i = 1 n λ i ∂ g i ∂ w i = 0 ∂ L ∂ a i = 2 λ i a i = 0 ∂ L ∂ λ i = g i ( w ) + a i 2 = 0 λ i ≥ 0 \left\{\begin{matrix}\frac{\partial L}{\partial w_i} = \frac{\partial f}{\partial w_i} + \displaystyle\sum_{i=1}^{n}\lambda _i\frac{\partial g_i}{\partial w_i} = 0 \\ \frac{\partial L}{\partial a_i} = 2\lambda _ia_i = 0 \\ \frac{\partial L}{\partial \lambda _i} = g_i(w) + a_i^2 = 0 \\ \lambda _i \ge 0\end{matrix}\right. ⎩ ⎨ ⎧∂wi∂L=∂wi∂f+i=1∑nλi∂wi∂gi=0∂ai∂L=2λiai=0∂λi∂L=gi(w)+ai2=0λi≥0
针对 λ i = 0 \lambda _i = 0 λi=0,有两种情况:
- λ i = 0 , a i ≠ 0 \lambda _i = 0, a_i \ne 0 λi=0,ai=0。由于 λ i = 0 \lambda _i = 0 λi=0,因此约束条件 g i ( w ) g_i(w) gi(w) 不起作用,且 g i ( w ) < 0 g_i(w) < 0 gi(w)<0。
- λ i ≠ 0 , a i = 0 \lambda _i \ne 0, a_i = 0 λi=0,ai=0。此时, g i ( w ) = 0 g_i(w) = 0 gi(w)=0 且 λ i > 0 \lambda _i > 0 λi>0,可以理解为约束条件 g i ( w ) g_i(w) gi(w) 起作用了,且 g i ( w ) = 0 g_i(w) = 0 gi(w)=0。
- 综合可得, λ i g i ( w ) = 0 \lambda _ig_i(w) = 0 λigi(w)=0,且在约束条件起作用时,有 λ i > 0 , g i ( w ) = 0 \lambda _i > 0, g_i(w) = 0 λi>0,gi(w)=0;在约束条件不起作用时,有 λ i = 0 , g i ( w ) < 0 \lambda _i = 0, g_i(w) < 0 λi=0,gi(w)<0。
由此,上述方程组转换为:
{ ∂ L ∂ w i = ∂ f ∂ w i + ∑ i = 1 n λ i ∂ g i ∂ w i = 0 λ i g i ( w ) = 0 g i ( w ) ≤ 0 λ i ≥ 0 \left\{\begin{matrix}\frac{\partial L}{\partial w_i} = \frac{\partial f}{\partial w_i} + \displaystyle\sum_{i=1}^{n}\lambda _i\frac{\partial g_i}{\partial w_i} = 0 \\ \lambda _ig_i(w) = 0 \\ g_i(w) \leq 0 \\ \lambda _i \ge 0\end{matrix}\right. ⎩ ⎨ ⎧∂wi∂L=∂wi∂f+i=1∑nλi∂wi∂gi=0λigi(w)=0gi(w)≤0λi≥0
以上便是不等式约束优化问题的 KKT(Karush-Kuhn-Tucker)条件, λ i \lambda _i λi 称为 KKT 乘子。上述式子直观地告诉我们,支持向量 g i ( w ) = 0 g_i(w) = 0 gi(w)=0,满足 λ i > 0 \lambda _i > 0 λi>0 即可;其他向量 g i ( w ) < 0 g_i(w) < 0 gi(w)<0,需满足 λ i = 0 \lambda _i = 0 λi=0。
根据最优化模型,我们要求的是:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 s . t . g i ( w ) = 1 − y i ( w T x i + b ) ≤ 0 i = 1 , 2 , . . . , n min \ \frac{1}{2}||w||^2 \\ s.t. \ \ g_i(w) = 1 - y_i(w^Tx_i + b) \leq 0 \ \ i = 1, 2, ..., n min 21∣∣w∣∣2s.t. gi(w)=1−yi(wTxi+b)≤0 i=1,2,...,n
即求 m i n L ( w , λ , a ) min \ L(w, \lambda, a) min L(w,λ,a), L ( w , λ , a ) L(w, \lambda, a) L(w,λ,a) 写成如下:
L ( w , λ , a ) = f ( w ) + ∑ i = 1 n λ i [ g i ( w ) + a i 2 ] = f ( w ) + ∑ i = 1 n λ i g i ( w ) + ∑ i = 1 n λ i a i 2 L(w, \lambda , a) = f(w) + \displaystyle\sum_{i=1}^{n}\lambda _i[g_i(w) + a_i^2] = f(w) + \displaystyle\sum_{i=1}^{n}\lambda _ig_i(w) + \displaystyle\sum_{i=1}^{n}\lambda _ia_i^2 L(w,λ,a)=f(w)+i=1∑nλi[gi(w)+ai2]=f(w)+i=1∑nλigi(w)+i=1∑nλiai2
由于 ∑ i = 1 n λ i a i 2 ≥ 0 \displaystyle\sum_{i=1}^{n}\lambda _ia_i^2 \ge 0 i=1∑nλiai2≥0,故我们可以将上述问题转化为求 m i n L ( w , λ ) min \ L(w, \lambda) min L(w,λ),如下所示:
L ( w , λ ) = f ( w ) + ∑ i = 1 n λ i g i ( w ) L(w, \lambda) = f(w) + \displaystyle\sum_{i=1}^{n}\lambda _ig_i(w) L(w,λ)=f(w)+i=1∑nλigi(w)
假设目标函数找到了最佳参数,并取得了最小值 p > 0 p > 0 p>0,即 m i n 1 2 ∣ ∣ w ∣ ∣ 2 = p min \ \frac{1}{2}||w||^2 = p min 21∣∣w∣∣2=p。根据上述可知, λ i ≥ 0 , g i ( w ) ≤ 0 , ∑ i = 1 n λ i g i ( w ) ≤ 0 \lambda _i \ge 0, g_i(w) \leq 0, \displaystyle\sum_{i=1}^{n}\lambda _ig_i(w) \leq 0 λi≥0,gi(w)≤0,i=1∑nλigi(w)≤0,因此 m i n L ( w , λ ) = m i n f ( w ) + m i n ∑ i = 1 n λ i g i ( w ) = p + m i n ∑ i = 1 n λ i g i ( w ) min \ L(w, \lambda) = min \ f(w) + min \ \displaystyle\sum_{i=1}^{n}\lambda _ig_i(w) = p + min \ \displaystyle\sum_{i=1}^{n}\lambda _ig_i(w) min L(w,λ)=min f(w)+min i=1∑nλigi(w)=p+min i=1∑nλigi(w)。而要使得 ∑ i = 1 n λ i g i ( w ) \displaystyle\sum_{i=1}^{n}\lambda _ig_i(w) i=1∑nλigi(w) 最小,就要使得 λ i \lambda_i λi 最大。故最优化问题可转化为如下:
m i n L ( w , λ ) = min w max λ L ( w , λ ) s . t . λ i ≥ 0 min \ L(w, \lambda) = \min_{w}{\max_{\lambda}{L(w, \lambda)}} \ \ s.t. \ \ \lambda _i \ge 0 min L(w,λ)=wminλmaxL(w,λ) s.t. λi≥0
强对偶性
对偶问题就是将以下式子:
min w max λ L ( w , λ ) s . t . λ i ≥ 0 \min_{w}{\max_{\lambda}{L(w, \lambda)}} \ \ s.t. \ \ \lambda _i \ge 0 wminλmaxL(w,λ) s.t. λi≥0
变成了以下式子:
max λ min w L ( w , λ ) s . t . λ i ≥ 0 \max_{\lambda}{\min_{w}{L(w, \lambda)}} \ \ s.t. \ \ \lambda _i \ge 0 λmaxwminL(w,λ) s.t. λi≥0
假设对于函数 f ( x ) f(x) f(x),有:
m i n m a x f ( x ) ≥ m a x m i n f ( x ) min \ max \ f(x) \ge max \ min \ f(x) min max f(x)≥max min f(x)
也就是说,从最大的里面挑出来最小的也要比从最小的里面挑出来最大的大,这就是弱对偶关系,当且仅当等号成立时,满足强对偶关系。
满足以下两点,强对偶关系便能成立:
- 对目标函数进行的优化属于凸优化问题。凸优化问题的定义:求取最小值的目标函数为凸函数的一类优化问题。
- 满足 KKT 条件,KKT 条件是强对偶性的充要条件。
SVM 优化
我们已知 SVM 的优化问题为:
min w 1 2 ∣ ∣ w ∣ ∣ 2 s . t . g i ( w , b ) = 1 − y i ( w T x i + b ) ≤ 0 i = 1 , 2 , . . . , n \min_w \ \frac{1}{2}||w||^2 \\ s.t. \ \ g_i(w, b) = 1 - y_i(w^Tx_i + b) \leq 0 \ \ \ \ i = 1, 2, ..., n wmin 21∣∣w∣∣2s.t. gi(w,b)=1−yi(wTxi+b)≤0 i=1,2,...,n
求解线性可分的 SVM 分类器的步骤为:
-
构造拉格朗日函数:
min w , b max λ L ( w , b , λ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 n λ i [ 1 − y i ( w T x i + b ) ] s . t . λ i ≥ 0 \min_{w, b}{\max_{\lambda}{L(w, b, \lambda)}} = \frac{1}{2}||w||^2 + \displaystyle\sum_{i=1}^{n}\lambda _i[1 - y_i(w^Tx_i + b)] \ \ s.t. \ \ \lambda _i \ge 0 w,bminλmaxL(w,b,λ)=21∣∣w∣∣2+i=1∑nλi[1−yi(wTxi+b)] s.t. λi≥0 -
利用强对偶性进行转化(便于后续求导等操作):
min w , b max λ L ( w , b , λ ) = max λ min w , b L ( w , b , λ ) \min_{w, b}{\max_{\lambda}{L(w, b, \lambda)}} = \max_{\lambda}{\min_{w, b}{L(w, b, \lambda)}} w,bminλmaxL(w,b,λ)=λmaxw,bminL(w,b,λ) -
固定 λ \lambda λ,分别对参数 w w w 和参数 b b b 求偏导( L ( w , b , λ ) L(w, b, \lambda) L(w,b,λ) 关于 w 、 b w、b w、b 最小化):
∂ L ∂ w = w − ∑ i = 1 n λ i x i y i = 0 ∂ L ∂ b = ∑ i = 1 n λ i y i = 0 \frac{\partial L}{\partial w} = w - \displaystyle\sum_{i=1}^{n}\lambda _ix_iy_i = 0 \\\frac{\partial L}{\partial b} = \displaystyle\sum_{i=1}^{n}\lambda _iy_i = 0 ∂w∂L=w−i=1∑nλixiyi=0∂b∂L=i=1∑nλiyi=0 -
将上述结果带回到拉格朗日函数:
L ( w , b , λ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 n λ i [ 1 − y i ( w T x i + b ) ] = 1 2 w T w + ∑ i = 1 n λ i − w T ∑ i = 1 n λ i y i x i − b ∑ i = 1 n λ i y i = 1 2 w T ∑ i = 1 n λ i y i x i − w T ∑ i = 1 n λ i y i x i − b ⋅ 0 + ∑ i = 1 n λ i = ∑ i = 1 n λ i − 1 2 ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j x i T x j L(w, b, \lambda) = \frac{1}{2}||w||^2 + \displaystyle\sum_{i=1}^{n}\lambda _i[1 - y_i(w^Tx_i + b)] \\ = \frac{1}{2}w^Tw + \displaystyle\sum_{i=1}^{n}\lambda _i - w^T\displaystyle\sum_{i=1}^{n}\lambda _iy_ix_i - b\displaystyle\sum_{i=1}^{n}\lambda _iy_i \\ = \frac{1}{2}w^T\displaystyle\sum_{i=1}^{n}\lambda _iy_ix_i - w^T\displaystyle\sum_{i=1}^{n}\lambda _iy_ix_i - b · 0 + \displaystyle\sum_{i=1}^{n}\lambda _i \\ = \displaystyle\sum_{i=1}^{n}\lambda _i - \frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n}\lambda_i\lambda_jy_iy_jx_i^Tx_j L(w,b,λ)=21∣∣w∣∣2+i=1∑nλi[1−yi(wTxi+b)]=21wTw+i=1∑nλi−wTi=1∑nλiyixi−bi=1∑nλiyi=21wTi=1∑nλiyixi−wTi=1∑nλiyixi−b⋅0+i=1∑nλi=i=1∑nλi−21i=1∑nj=1∑nλiλjyiyjxiTxj
此时, L ( w , b , λ ) L(w, b, \lambda) L(w,b,λ) 只存在一个变量,即 λ \lambda λ。 -
内部的最小值求解完成,接着求解外部的最大值:
max λ [ ∑ i = 1 n λ i − 1 2 ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j x i T x j ] s . t . ∑ i = 1 n λ i y i = 0 λ i ≥ 0 \max_\lambda \ [\displaystyle\sum_{i=1}^{n}\lambda _i - \frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n}\lambda_i\lambda_jy_iy_jx_i^Tx_j] \\s.t. \ \ \displaystyle\sum_{i=1}^{n}\lambda _iy_i = 0 \\\lambda _i \ge 0 λmax [i=1∑nλi−21i=1∑nj=1∑nλiλjyiyjxiTxj]s.t. i=1∑nλiyi=0λi≥0
优化问题变成了上述形式,这是一个二次规划问题,对于此类问题,常用序列最小优化(Sequential Minimal Optimization,SMO)算法进行求解。SMO 算法的核心思想非常简单,每次只优化一个参数,而固定住其他参数,仅求解当前这个优化参数的极值。
SMO 算法每次只优化一个参数,但我们的目标函数有约束条件 ∑ i = 1 n λ i y i = 0 \displaystyle\sum_{i=1}^{n}\lambda _iy_i = 0 i=1∑nλiyi=0,没法一次只变动一个参数,所以我们选择一次变动两个参数。具体步骤如下:
-
选择两个需要更新的参数 λ i 、 λ j \lambda _i、\lambda _j λi、λj,固定其他参数,于是得到以下约束:
λ i y i + λ j y j = c λ i ≥ 0 , λ j ≥ 0 \lambda _iy_i + \lambda_jy_j = c \ \ \ \ \lambda _i \ge 0, \ \lambda _j \ge 0 λiyi+λjyj=c λi≥0, λj≥0
其中 c = − ∑ k ≠ i , j λ k y k c = -\displaystyle\sum_{k \ne {i, j}}\lambda _ky_k c=−k=i,j∑λkyk,由此得出 λ j = c − λ i y i y i \lambda_j = \frac{c - \lambda_iy_i}{y_i} λj=yic−λiyi,也就是说,我们可以用 λ i \lambda _i λi 的表达式替代 λ j \lambda _j λj,这样就相当于把目标问题转化成了仅有一个约束条件 λ i ≥ 0 \lambda_i \ge 0 λi≥0 的最优化问题。 -
对于仅有一个约束条件的最优化问题,可以对 λ i \lambda _i λi 进行求偏导,令导数为零,求出变量值 λ i _ n e w \lambda _{i\_{new}} λi_new,然后根据 λ i _ n e w \lambda _{i\_{new}} λi_new 求出 λ j _ n e w \lambda _{j\_{new}} λj_new。
-
多次迭代,直至收敛。
通过 SMO 算法求得最优解 λ ∗ \lambda ^* λ∗。
-
-
构造最大间隔超平面:
w = ∑ i = 1 n λ i y i x i 1 − y i ( w T x i + b ) = 0 w = \displaystyle\sum_{i=1}^{n}\lambda _iy_ix_i \\1 - y_i(w^Tx_i + b) = 0 w=i=1∑nλiyixi1−yi(wTxi+b)=0
w w w 是已经求得的。我们知道所有 λ i > 0 \lambda _i > 0 λi>0 对应的点都是支持向量,那么我们可以随便找个支持向量,将其代入式子 1 − y s ( w T x s + b ) = 0 1 - y_s(w^Tx_s + b) = 0 1−ys(wTxs+b)=0,两边同乘 y s y_s ys,因为 y s 2 = 1 y_s^2 = 1 ys2=1,因此得到 b = y s − w T x s b = y_s - w^Tx_s b=ys−wTxs。为了更具鲁棒性,可以求得支持向量的均值:
b = 1 ∣ S ∣ ∑ s ∈ S ( y s − w T x s ) b = \frac{1}{|S|}\displaystyle\sum_{s \in S}(y_s - w^Tx_s) b=∣S∣1s∈S∑(ys−wTxs)
至此, w w w 和 b b b 均已求出。进而构造出最大间隔超平面 w T x + b = 0 w^Tx + b = 0 wTx+b=0。
分类决策函数 f ( x ) = s i g n ( w T x + b ) f(x) = sign(w^Tx + b) f(x)=sign(wTx+b),其中 s i g n ( ⋅ ) sign(·) sign(⋅) 为阶跃函数:
s i g n ( x ) = { − 1 x < 0 0 x = 0 1 x > 0 sign(x) = \left\{\begin{matrix} -1 & x < 0 \\ 0 & x = 0 \\ 1 & x > 0 \end{matrix}\right. sign(x)=⎩ ⎨ ⎧−101x<0x=0x>0
将新样本点导入到决策函数中,即可得到样本的分类结果。
软间隔
解决问题
在实际应用中,完全线性可分的样本集是很少的,如果遇到了无法实现完全线性可分的样本集,该怎么办?如下图所示:

为了解决上述问题,就提出了软间隔,相比于硬间隔的苛刻条件,软间隔允许个别样本点出现在间隔带里面。也就是说,我们允许部分样本点不满足约束条件 1 − y i ( w T x i + b ) ≤ 0 1 - y_i(w^Tx_i + b) \leq 0 1−yi(wTxi+b)≤0。为了度量这个间隔软到何种程度,我们为每个样本引入了一个松弛变量 ξ i \xi _i ξi,令 ξ i ≥ 0 \xi _i \ge 0 ξi≥0,且 1 − y i ( w T x i + b ) − ξ i ≤ 0 1 - y_i(w^Tx_i + b) - \xi _i \leq 0 1−yi(wTxi+b)−ξi≤0。如下图所示:

优化目标及求解
增加软间隔后,优化目标就变成了如下:
min w 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i s . t . g i ( w , b ) = 1 − y i ( w T x i + b ) − ξ i ≤ 0 ξ i ≥ 0 , i = 1 , 2 , . . . , n \min_w \ \frac{1}{2}||w||^2 + C\displaystyle\sum_{i=1}^{n}\xi _i \\ s.t. \ \ g_i(w, b) = 1 - y_i(w^Tx_i + b) - \xi _i \leq 0 \ \ \ \ \xi _i \ge 0, \ \ i = 1, 2, ..., n wmin 21∣∣w∣∣2+Ci=1∑nξis.t. gi(w,b)=1−yi(wTxi+b)−ξi≤0 ξi≥0, i=1,2,...,n
其中, C C C 是一个大于 0 0 0 的常数(惩罚参数),可以理解为对错误样本的惩罚程度。若 C C C 为无穷大, ξ i \xi _i ξi 必然为无穷小,如此一来线性 SVM 就又变成了线性可分,当 C C C 为有限值时,才会允许部分样本不遵循约束条件。
接下来,我们将针对新的优化目标进行最优化问题求解,求解步骤如下:
-
构造拉个朗日函数:
min w , b , ξ max λ , μ L ( w , b , ξ , λ , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i + ∑ i = 1 n λ i [ 1 − ξ i − y i ( w T x i + b ) ] − ∑ i = 1 n μ i ξ i s . t . λ i ≥ 0 μ i ≥ 0 \min_{w, b, \xi}{\max_{\lambda, \mu}{L(w, b, \xi, \lambda, \mu)}} = \frac{1}{2}||w||^2 + C\displaystyle\sum_{i=1}^{n}\xi _i + \displaystyle\sum_{i=1}^{n}\lambda _i[1 - \xi _i - y_i(w^Tx_i + b)] - \displaystyle\sum_{i=1}^{n}\mu _i\xi _i \\ s.t. \ \ \lambda _i \ge 0 \ \ \ \ \mu _i \ge 0 w,b,ξminλ,μmaxL(w,b,ξ,λ,μ)=21∣∣w∣∣2+Ci=1∑nξi+i=1∑nλi[1−ξi−yi(wTxi+b)]−i=1∑nμiξis.t. λi≥0 μi≥0
其中, λ i 、 μ i \lambda_i、\mu_i λi、μi 是拉格朗日乘子, w 、 b 、 μ i w、b、\mu_i w、b、μi 是优化问题的参数。 -
利用强对偶性进行转化:
min w , b , ξ max λ , μ L ( w , b , ξ , λ , μ ) = max λ , μ min w , b , ξ L ( w , b , ξ , λ , μ ) \min_{w, b, \xi}{\max_{\lambda, \mu}{L(w, b, \xi, \lambda, \mu)}} = \max_{\lambda, \mu}{\min_{w, b, \xi}{L(w, b, \xi, \lambda, \mu)}} w,b,ξminλ,μmaxL(w,b,ξ,λ,μ)=λ,μmaxw,b,ξminL(w,b,ξ,λ,μ) -
分别对参数 w 、 b 、 ξ i w、b、\xi_i w、b、ξi 求偏导,并令偏导为零,得到如下关系:
w = ∑ i = 1 n λ i y i x i 0 = ∑ i = 1 n λ i y i C = λ i + μ i w = \displaystyle\sum_{i=1}^{n}\lambda _iy_ix_i \\ 0 = \displaystyle\sum_{i=1}^{n}\lambda _iy_i \\ C = \lambda_i + \mu_i w=i=1∑nλiyixi0=i=1∑nλiyiC=λi+μi -
将上述结果带回到拉格朗日函数:
min w , b , ξ L ( w , b , ξ , λ , μ ) = ∑ i = 1 n λ i − 1 2 ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j x i T x j \min _{w, b, \xi} \ L(w, b, \xi, \lambda, \mu) = \displaystyle\sum_{i=1}^{n}\lambda _i - \frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n}\lambda_i\lambda_jy_iy_jx_i^Tx_j w,b,ξmin L(w,b,ξ,λ,μ)=i=1∑nλi−21i=1∑nj=1∑nλiλjyiyjxiTxj
最小化结果只有 λ \lambda λ,而没有 μ \mu μ,所以只需要最大化 λ \lambda λ 就好。 -
内部的最小值求解完成,接着求解外部的最大值:
max λ [ ∑ i = 1 n λ i − 1 2 ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j x i T x j ] s . t . ∑ i = 1 n λ i y i = 0 λ i ≥ 0 C − λ i − μ i = 0 \max_\lambda \ [\displaystyle\sum_{i=1}^{n}\lambda _i - \frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n}\lambda_i\lambda_jy_iy_jx_i^Tx_j] \\s.t. \ \ \displaystyle\sum_{i=1}^{n}\lambda _iy_i = 0 \\\lambda _i \ge 0 \\C - \lambda_i - \mu_i = 0 λmax [i=1∑nλi−21i=1∑nj=1∑nλiλjyiyjxiTxj]s.t. i=1∑nλiyi=0λi≥0C−λi−μi=0
可以发现,软间隔与硬间隔相似,只是多了个约束条件。利用 SMO 算法求解最优拉格朗日乘子 λ ∗ \lambda ^* λ∗。
-
构造最大间隔超平面:
w = ∑ i = 1 n λ i y i x i b = 1 ∣ S ∣ ∑ s ∈ S ( y s − w T x s ) w = \displaystyle\sum_{i=1}^{n}\lambda _iy_ix_i \\b = \frac{1}{|S|}\displaystyle\sum_{s \in S}(y_s - w^Tx_s) w=i=1∑nλiyixib=∣S∣1s∈S∑(ys−wTxs)
将求得的 λ i \lambda_i λi 代入上式,得到 w w w 和 b b b,最终求得超平面 w T x + b = 0 w^Tx + b = 0 wTx+b=0。
核函数
线性不可分
上述讨论的硬间隔和软间隔都是在说样本集的完全线性可分或大部分线性可分,但是我们可能会碰到的一种情况是样本点不是线性可分的,如下图所示:

这种情况的解决办法就是,将二维空间中线性不可分的样本点映射到高维空间中,让样本点在高维空间中实现线性可分,如下图所示:

对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间里,再通过间隔最大化的方式,学习得到的支持向量机,就是非线性 SVM。
我们用 x x x 表示原来的样本点,用 ϕ ( x ) \phi (x) ϕ(x) 表示 x x x 映射到新的特征空间后得到的新向量,那么分隔的超平面可以表示为 f ( x ) = w ϕ ( x ) + b f(x) = w\phi (x) + b f(x)=wϕ(x)+b。
对于非线性 SVM,对偶问题就变成了如下:
min λ [ 1 2 ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j ( ϕ ( x i ) ⋅ ϕ ( x j ) ) − ∑ i = 1 n λ i ] s . t . ∑ i = 1 n λ i y i = 0 λ i ≥ 0 C − λ i − μ i = 0 \min_\lambda \ [\frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n}\lambda _i\lambda _jy_iy_j(\phi (x_i) · \phi (x_j)) - \displaystyle\sum_{i=1}^{n}\lambda _i] \\s.t. \ \ \displaystyle\sum_{i=1}^{n}\lambda _iy_i = 0 \\\lambda _i \ge 0 \\C - \lambda_i - \mu_i = 0 λmin [21i=1∑nj=1∑nλiλjyiyj(ϕ(xi)⋅ϕ(xj))−i=1∑nλi]s.t. i=1∑nλiyi=0λi≥0C−λi−μi=0
可以看到非线性 SVM 与线性 SVM 唯一的不同之处,就是之前的 ( x i ⋅ x j ) (x_i · x_j) (xi⋅xj) 变成了 ( ϕ ( x i ) ⋅ ϕ ( x j ) ) (\phi (x_i) · \phi (x_j)) (ϕ(xi)⋅ϕ(xj))。
核函数的作用
为什么需要核函数呢?这是因为低维空间映射到高维空间后,维度可能会很大,如果对全部样本进行点乘计算,可能会耗费很大的计算量。
但如果存在这样的一个核函数 k ( x , y ) = ( ϕ ( x i ) , ϕ ( x j ) ) k(x, y) = (\phi (x_i), \phi (x_j)) k(x,y)=(ϕ(xi),ϕ(xj)),使得 x i x_i xi 与 x j x_j xj 在特征空间的内积等于它们在原始样本空间中通过函数 k ( x , y ) k(x, y) k(x,y) 计算得到的结果,我们就不需要计算高维甚至无穷维空间的内积了。
举个例子,假设我们有一个多项式核函数:
k ( x , y ) = ( x ⋅ y + 1 ) 2 k(x, y) = (x · y + 1)^2 k(x,y)=(x⋅y+1)2
将样本点代入:
k ( x , y ) = ( ∑ i = 1 n ( x i ⋅ y i ) + 1 ) 2 k(x, y) = (\displaystyle\sum_{i=1}^{n}(x_i · y_i) + 1)^2 k(x,y)=(i=1∑n(xi⋅yi)+1)2
展开后:
∑ i = 1 n x i 2 y i 2 + ∑ i = 2 n ∑ j = 1 i − 1 ( 2 x i x j ) ( 2 y i y j ) + ∑ i = 1 n ( 2 x i ) ( 2 y i ) + 1 \displaystyle\sum_{i=1}^{n}x_i^2y_i^2 + \displaystyle\sum_{i=2}^{n}\displaystyle\sum_{j=1}^{i-1}(\sqrt 2x_ix_j)(\sqrt 2y_iy_j) + \displaystyle\sum_{i=1}^{n}(\sqrt 2x_i)(\sqrt 2y_i) + 1 i=1∑nxi2yi2+i=2∑nj=1∑i−1(2xixj)(2yiyj)+i=1∑n(2xi)(2yi)+1
如果没有核函数,则需要把原样本点向量映射为:
x ′ = ( x 1 2 , . . . , x n 2 , . . . , 2 x 1 , . . . , 2 x n , 1 ) x' = (x_1^2, ..., x_n^2, ..., \sqrt 2x_1, ..., \sqrt 2x_n, 1) x′=(x12,...,xn2,...,2x1,...,2xn,1)
再将其运用于内积计算,才能与多项式核函数达到相同的效果。
可见核函数的引入一方面减少了计算量,另一方面也减少了存储数据时的内存消耗。
常见核函数
常用的核函数有如下:
-
线性核函数:
k ( x i , x j ) = x i T x j k(x_i, x_j) = x_i^Tx_j k(xi,xj)=xiTxj -
多项式核函数:
k ( x i , x j ) = ( x i T x j ) d k(x_i, x_j) = (x_i^Tx_j)^d k(xi,xj)=(xiTxj)d -
高斯核函数:
k ( x i , x j ) = e − ∣ ∣ x i − x J ∣ ∣ 2 σ 2 k(x_i, x_j) = e^{-\frac{||x_i - x_J||}{2\sigma ^2}} k(xi,xj)=e−2σ2∣∣xi−xJ∣∣
上述是三个常用的核函数,其中只有高斯核函数是需要调参的。
SVM 算法优缺点
优点
- 有严格的数学理论支持,可解释性强,不依靠统计方法,从而简化了通常的分类和回归问题;
- 能找出对任务至关重要的关键样本(即支持向量);
- 采用核技巧之后,可以处理非线性分类/回归任务;
- 最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
缺点
-
训练时间长。当采用 SMO 算法时,由于每次都需要挑选一对参数,因此时间复杂度为 O ( N 2 ) O(N^2) O(N2),其中 N N N 为训练样本的数量;
-
当采用核技巧时,如果需要存储核矩阵,则空间复杂度为 O ( N 2 ) O(N^2) O(N2);
-
模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂度较高。
因此支持向量机目前只适合小批量样本的任务,无法适应百万甚至上亿样本的任务。