为什么 θ i \theta_i θi的取值会造成远程衰减性
旋转位置编码的出发点为:通过绝对位置编码的方式实现相对位置编码。
对词向量 q \boldsymbol{q} q添加绝对位置信息 m m m,希望找到一种函数 f f f,使得:
< f ( q , m ) , f ( k , n ) > = g ( q , k , m − n ) <f(\boldsymbol{q}, m), f(\boldsymbol{k}, n)> = g(\boldsymbol{q}, \boldsymbol{k}, m - n) <f(q,m),f(k,n)>=g(q,k,m−n)
假设词向量是二维的,借用复数来进行求解(具体求解过程参考:https://spaces.ac.cn/archives/8265),最终得到一种可行解:
f ( q , m ) = q e i m θ = ( c o s m θ − s i n m θ s i n m θ c o s m θ ) ( q 0 q 1 ) \begin{align} f(\boldsymbol{q}, m) &= \boldsymbol{q} e^{im \theta} \\ &= \left(\begin{matrix} cos\ m\theta& -sin\ m\theta\\ sin\ m\theta& cos\ m\theta \end{matrix} \right) \left(\begin{array}{c} q_0\\ q_1 \end{array} \right) \end{align} f(q,m)=qeimθ=(cos mθsin mθ−sin mθcos mθ)(q0q1)
扩展到多维:
f ( q , m ) = R m q f(\boldsymbol{q}, m) = \boldsymbol{R}_m \boldsymbol{q} f(q,m)=Rmq
R m = ( c o s m θ 0 − s i n m θ 0 0 0 ⋯ 0 0 s i n m θ 0 c o s m θ 0 0 0 ⋯ 0 0 0 0 c o s m θ 1 − s i n m θ 1 ⋯ 0 0 0 0 s i n m θ 1 c o s m θ 1 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 0 ⋯ c o s m θ d / 2 − 1 − s i n m θ d / 2 − 1 0 0 0 0 ⋯ s i n m θ d / 2 − 1 c o s m θ d / 2 − 1 ) \boldsymbol{R}_m = \left(\begin{matrix} cos\ m\theta_0& -sin\ m\theta_0& 0& 0& \cdots& 0& 0\\ sin\ m\theta_0& cos\ m\theta_0& 0& 0& \cdots& 0& 0\\ 0& 0& cos\ m\theta_1& -sin\ m\theta_1& \cdots& 0& 0\\ 0& 0& sin\ m\theta_1& cos\ m\theta_1& \cdots& 0& 0\\ \vdots& \vdots& \vdots& \vdots& \ddots& \vdots& \vdots\\ 0& 0& 0& 0& \cdots& cos\ m\theta_{d/2 - 1}& -sin\ m\theta_{d/2-1}\\ 0& 0& 0& 0& \cdots& sin\ m\theta_{d/2 - 1}& cos\ m\theta_{d/2-1}\\ \end{matrix}\right) Rm= cos mθ0sin mθ000⋮00−sin mθ0cos mθ000⋮0000cos mθ1sin mθ1⋮0000−sin mθ1cos mθ1⋮00⋯⋯⋯⋯⋱⋯⋯0000⋮cos mθd/2−1sin mθd/2−10000⋮−sin mθd/2−1cos mθd/2−1
相当于左乘一个旋转矩阵,或者说高维向量,每两维一组,分别旋转一个角度,且不改变模长。
显然, ( R m q ) T ( R n k ) = q T R m T R n k = q T R n − m k (\boldsymbol{R}_m \boldsymbol{q})^{T} (\boldsymbol{R}_n \boldsymbol{k})= \boldsymbol{q}^T \boldsymbol{R}_m^T \boldsymbol{R}_n \boldsymbol{k} = \boldsymbol{q}^T \boldsymbol{R}_{n-m} \boldsymbol{k} (Rmq)T(Rnk)=qTRmTRnk=qTRn−mk,这样Attention就包含相对位置信息了。
下面分析为什么 θ i \theta_i θi的取值会造成远程衰减性
远程衰减性指的是,对于两个词向量,如果两者相对距离较近,那么它们的注意力分数应该偏高,反之应该偏低。
假设 q \boldsymbol{q} q和 k \boldsymbol{k} k均为ones向量,则 ( R m q ) T ( R n k ) = q T R n − m k = 2 ∑ i = 0 d / 2 − 1 c o s ( n − m ) θ i (\boldsymbol{R}_m \boldsymbol{q})^{T} (\boldsymbol{R}_n \boldsymbol{k})= \boldsymbol{q}^T \boldsymbol{R}_{n-m} \boldsymbol{k} = 2\sum_{i=0}^{d/2-1} cos\ (n-m)\theta_i (Rmq)T(Rnk)=qTRn−mk=2∑i=0d/2−1cos (n−m)θi,设相对距离 n − m n-m n−m为 x x x,则相对距离为 x x x的向量之间注意力得分:
g ( x ) = 2 ∑ i = 0 d / 2 − 1 c o s x θ i g(x) = 2\sum_{i=0}^{d/2-1} cos\ x\theta_i g(x)=2i=0∑d/2−1cos xθi
如果任意 θ i = 0 \theta_i=0 θi=0,则 g ( x ) = d g(x)=d g(x)=d,无论相对距离多大,注意力得分都相等
如果任意 θ i = 1 \theta_i=1 θi=1,则 g ( x ) = d c o s x g(x)=d\ cos\ x g(x)=d cos x,随着相对距离增大,注意力得分呈周期性变化,但不会震荡衰减:
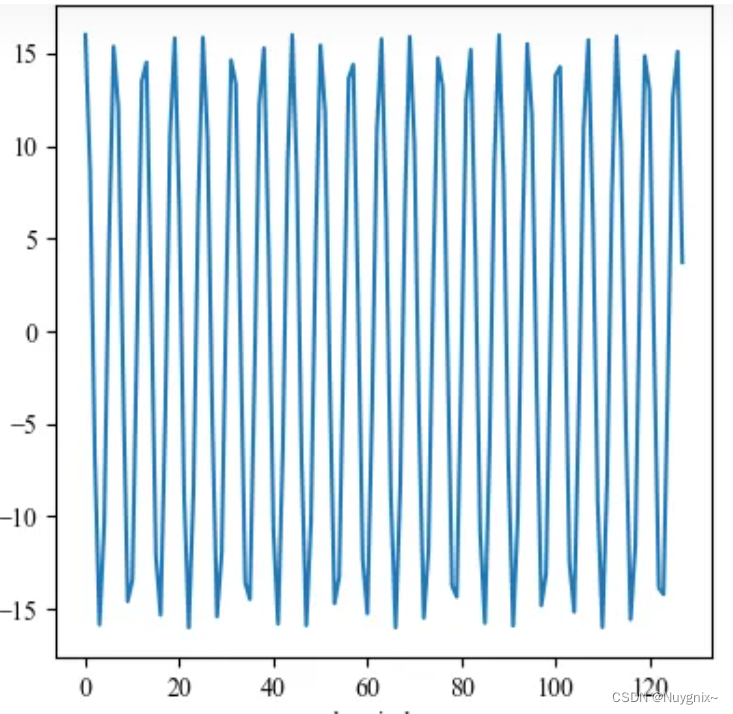
而作者在 θ i \theta_i θi的选择上,沿用了Sinusoidal位置编码的方案,即 θ i = 1000 0 − 2 i / d \theta_i=10000^{-2i/d} θi=10000−2i/d,它会带来一定的远程衰减性。
每个 θ i \theta_i θi, c o s x θ i cos\ x\theta_i cos xθi的周期大小 T i T_i Ti等于 2 π θ i = 2 π 1000 0 − 2 i / d = 2 π ∗ 1 0 8 i / d \frac{2\pi}{\theta_i} = \frac{2\pi}{10000^{-2i/d}} = 2\pi*10^{8i/d} θi2π=10000−2i/d2π=2π∗108i/d,所以 i i i越大, T i T_i Ti越大,最小周期为 T 0 = 2 π T_0 = 2\pi T0=2π,最大周期为 T d / 2 − 1 = 2 π ∗ 1 0 ( 4 − 8 d ) T_{d/2-1} = 2\pi*10^{(4-\frac{8}{d})} Td/2−1=2π∗10(4−d8)。
如果对于所有的 x x x, x < 1 4 T d / 2 − 1 = π 2 ∗ 1 0 ( 4 − 8 d ) x<\frac{1}{4}T_{d/2-1}=\frac{\pi}{2}*10^{(4-\frac{8}{d})} x<41Td/2−1=2π∗10(4−d8),也就是说, c o s x θ d / 2 − 1 cos\ x\theta_{d/2-1} cos xθd/2−1处于单调递减区间(下方的蓝色区间)
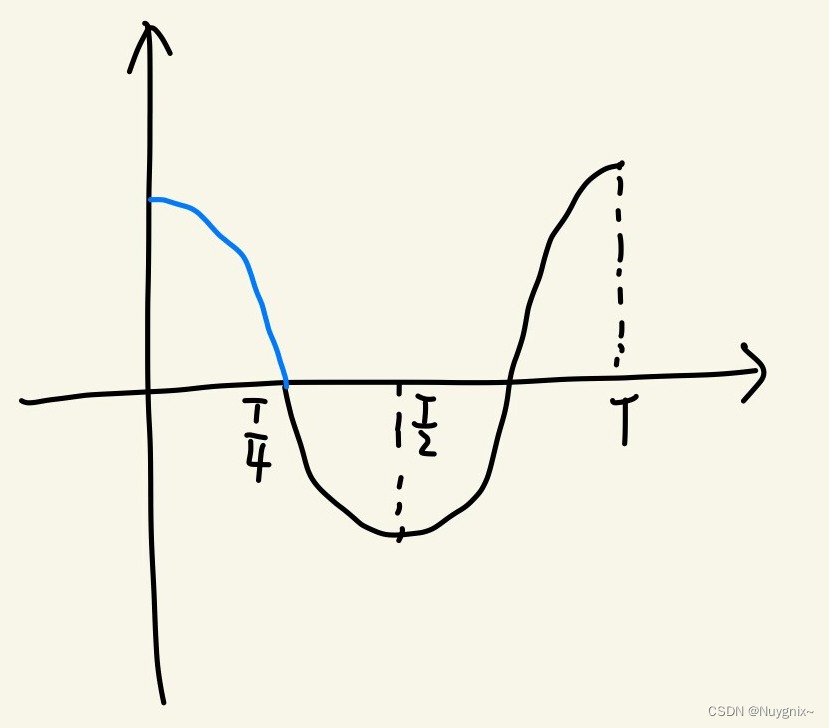
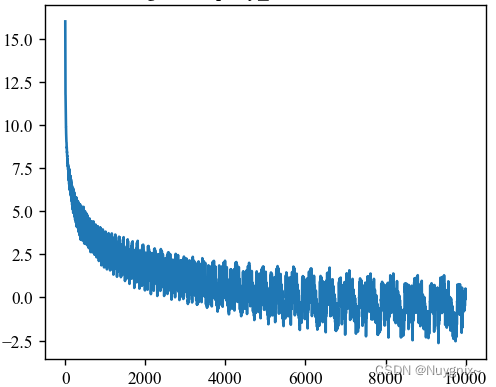
由于前面的 c o s x θ i cos x\theta_i cosxθi呈周期变化,而周期变化的函数 + 单调递减的函数 = 震荡递减的函数。因此,注意力得分 g ( x ) g(x) g(x)随着相对距离 x x x的增大而震荡减小。
比如在LLaMA中, d = 4096 d=4096 d=4096, 1 4 T d / 2 − 1 \frac{1}{4}T_{d/2-1} 41Td/2−1近似于 1 0 4 10^4 104,由于实际应用中,最大序列长度一般不会大于 1 0 4 10^4 104,所以相对距离 x < 1 4 T d / 2 − 1 x<\frac{1}{4}T_{d/2-1} x<41Td/2−1一般是成立的,当然,也可以增大 θ i = 1000 0 − 2 i / d \theta_i=10000^{-2i/d} θi=10000−2i/d中的10000,这样 T d / 2 − 1 T_{d/2-1} Td/2−1会变得更大。
当 d = 4 d=4 d=4时,最大周期 T d / 2 − 1 T_{d/2-1} Td/2−1是628,下面的示例 x x x会超过 1 4 T d / 2 − 1 \frac{1}{4}T_{d/2-1} 41Td/2−1,因此 g ( x ) g(x) g(x)呈周期性,并不是震荡减小
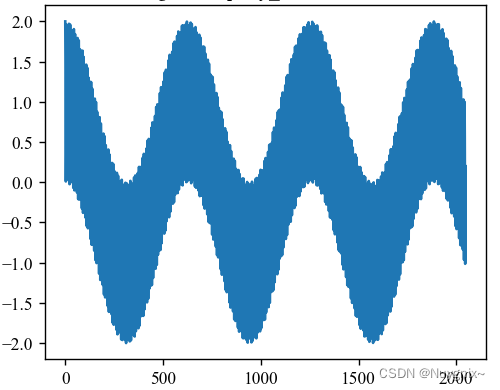
当 d = 256 d=256 d=256时,下面的示例 x x x不超过 1 4 T d / 2 − 1 = 14617 \frac{1}{4}T_{d/2-1}=14617 41Td/2−1=14617,因此震荡减小。