个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题

 http://t.csdnimg.cn/yUl2I   

【C++】         

 http://t.csdnimg.cn/6AbpV 

数据结构与算法

 http://t.csdnimg.cn/hKh2l

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

括号生成

题目链接：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

题目

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

• 1 <= n <= 8

解法

题目解析

题目的意思非常简单，给定我们一个数字 n 用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

算法原理思路讲解 

我们要解决这道题目，首先要知道的是什么是有效的括号，首先有效的括号应该符合下面两点

• 总的左括号数量等于总的右括号数量（左括号数量 == 总的右括号数量）
• 从头开始的任意一个子串，总的左括号的数量都大于等于总的右括号的数量

• 放⼊左括号时需判断此时左括号数量是否⼩于字符串总⻓度的⼀半（若左括号的数量⼤于等于字符串⻓度的⼀半时继续放置左括号，则左括号的总数量⼀定⼤于右括号的总数量）；
• 放⼊右括号时需判断此时右括号数量是否⼩于左括号数量。

并且由题目意思可以的到，需要填入的空为 2n，那么我们便可以设计出决策树来了。

我们可以一共选择 2n 次，将不符合有效的括号的剪枝掉。

一、画出决策树

以 n=2 为例子

​

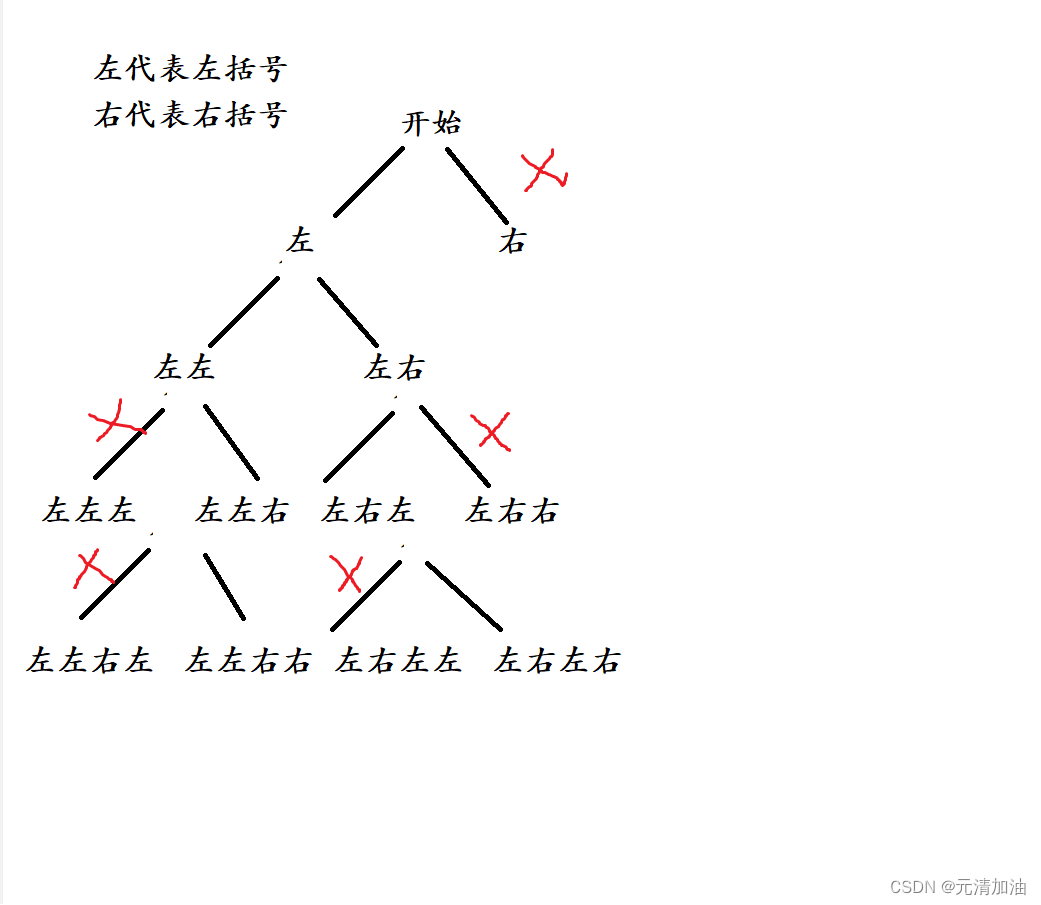
决策树就是我们后面设计函数的思路

二、设计代码

（1）全局变量

int left,right,sum;
string path;
vector<string> ret;

• left（当前状态的字符串中的左括号数量） 
• right（当前状态的字符串中的右括号数量）
• sum（总的左右括号最多的数量） 
• path（记录路径的左右括号）
• ret（存放所有有效括号的可能）

（2）设计递归函数

void dfs();

• 参数：无；
• 返回值：⽆；
• 函数作⽤：查找所有合理的括号序列并存储在答案列表中

1.  递归结束条件：当前状态右括号⻓度与 n 相等，记录当前状态并返回；
2. 若此时左括号数量⼩于 n ，则在当前状态的字符串末尾添加左括号并继续递归， 递归结束撤销添加操作；
3. 若此时右括号数量⼩于左括号数量（右括号数量可以由当前状态的字符串⻓度减去左括号数量求得），则在当前状态的字符串末尾添加右括号并递归，递归结束撤销添加操作； 

以上思路讲解完毕，大家可以自己做一下了

  代码实现

• 空间复杂度：O(n)，除了答案数组之外，我们所需要的空间取决于递归栈的深度，每一层递归函数需要 O(1) 的空间，最多递归 2n 层，因此空间复杂度为 O(n)

class Solution {
public:int left,right,sum;string path;vector<string> ret;void dfs(){if (right == sum){ret.push_back(path);return;}if (left < sum){path.push_back('(');left++;dfs();path.pop_back();left--;}if (right < left){path.push_back(')');right++;dfs();path.pop_back();right--;}}vector<string> generateParenthesis(int n) {sum = n;dfs();return ret;}
};