【等差数列
⟹ \Longrightarrow ⟹ 通项公式: a n = a 1 + ( n − 1 ) d = a m + ( n − m ) d = n d + a 1 − d = A n + B a_n= a_1+(n-1)d =a_m+(n-m)d=nd+a_1-d=An+B an=a1+(n−1)d=am+(n−m)d=nd+a1−d=An+B ⟹ \Longrightarrow ⟹ A = d , B = a 1 − d A=d,B=a_1-d A=d,B=a1−d
⟹ \Longrightarrow ⟹ 求和公式: S n = n ( a 1 + a n ) 2 = n a n + 1 2 ( n 为偶数时,可虚拟小数) = n a 1 + n ( n − 1 ) 2 d = d 2 n 2 + ( a 1 − d 2 ) n = C n 2 + D n S_n=\frac{n(a_1+a_n)}{2}=na_{\frac{n+1}{2}}(n为偶数时,可虚拟小数)=na_1+\frac{n(n-1)}{2}d=\frac{d}{2}n^2+(a_1-\frac{d}{2})n=Cn^2+Dn Sn=2n(a1+an)=na2n+1(n为偶数时,可虚拟小数)=na1+2n(n−1)d=2dn2+(a1−2d)n=Cn2+Dn ⟹ \Longrightarrow ⟹ C = d 2 , D = a 1 − d 2 C=\frac{d}{2},D=a_1-\frac{d}{2} C=2d,D=a1−2d
其中,
S n = n a n + 1 2 S_n=na_{\frac{n+1}{2}} Sn=na2n+1 ⟹ \Longrightarrow ⟹ 相同的奇数项和之比 a k b k \frac{a_k}{b_k} bkak= S 2 k − 1 T 2 k − 1 \frac{S_{2k-1}}{T_{2k-1}} T2k−1S2k−1
S n = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2dn2+(a1−2d)n ⟹ \Longrightarrow ⟹ 对称轴为 n = − a 1 − d 2 2 × d 2 = 1 2 − a 1 d n=-\frac{a_1-\frac{d}{2}}{2×\frac{d}{2}}=\frac{1}{2}-\frac{a_1}{d} n=−2×2da1−2d=21−da1,最值取在最靠近对称轴的整数处
⟹ \Longrightarrow ⟹下标和:+
⟹ \Longrightarrow ⟹连续等长片段和/前n项和:新公差为 d n 2 dn^2 dn2
⟹ \Longrightarrow ⟹ 偶数项和与奇数项和之比:
若等差数列一共有 2 n 2n 2n项,则 S 偶 − S 奇 = n d , S 偶 S 奇 = a n + 1 a n S_偶-S_奇=nd,\frac{S_偶}{S_奇}=\frac{a_{n+1}}{a_n} S偶−S奇=nd,S奇S偶=anan+1。
若等差数列一共有 2 n — 1 2n—1 2n—1项,则 S 奇 − S 偶 = a n + 1 S_奇-S_偶=a_{n+1} S奇−S偶=an+1, S 奇 S 偶 = n n − 1 \frac{S_奇}{S_偶}=\frac{n}{n-1} S偶S奇=n−1n, S 2 n − 1 = S 奇 + S 偶 = ( 2 n − 1 ) a n S_{2n-1}=S_奇+S_偶=(2n-1)a_n S2n−1=S奇+S偶=(2n−1)an
⟹ \Longrightarrow ⟹ a n a_n an与 S n S_n Sn的快速转换: S n S_n Sn的二次项系数是 a n a_n an一次项系数的一半, a n a_n an的一次项系数是 S n S_n Sn二次项系数的二倍
⟹ \Longrightarrow ⟹ 轮换对称性
⟹ \Longrightarrow ⟹ 判定等差数列:①定义法: a n − a n − 1 = d a_n-a_{n-1}=d an−an−1=d;②通项形如 a n = A n + B a_n=An+B an=An+B;③前n项和形如 S n − C n 2 + D n S_n-Cn^2+Dn Sn−Cn2+Dn】
类比记忆法:牢记等差,引出等比
【等比数列
⟹ \Longrightarrow ⟹ 通项公式: a n = a 1 q n − 1 = a m q n − m = a k q n − k = a 1 q q n a_n=a_1q^{n-1}=a_mq^{n-m}=a_kq^{n-k}=\frac{a_1}{q}q^n an=a1qn−1=amqn−m=akqn−k=qa1qn
⟹ \Longrightarrow ⟹ 前n项和公式:当q=1时, S n = n a 1 ;当 q ≠ 1 时, S n = a 1 ( 1 − q n ) 1 − q = a 1 − a n q 1 − q = a 1 − a n + 1 1 − q S_n=na_1;当q≠1时,S_n=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_nq}{1-q}=\frac{a_1-a_{n+1}}{1-q} Sn=na1;当q=1时,Sn=1−qa1(1−qn)=1−qa1−anq=1−qa1−an+1
⟹ \Longrightarrow ⟹下标和:×
⟹ \Longrightarrow ⟹ 连续等长片段和:新公比为 q n q^n qn
⟹ \Longrightarrow ⟹ 偶数项和与奇数项和之比:
若等比数列一共有 2 n 2n 2n项,则 S 偶 S 奇 = q \frac{S_偶}{S_奇}=q S奇S偶=q。
若等比数列一共有 2 n 一 1 2n一1 2n一1项,则 S 奇 S_奇 S奇与 S 偶 S_偶 S偶之间的关系无规律。】
【莫名巧合:等差数列
通项公式: a n = A n + B a_n=An+B an=An+B ⟹ \Longrightarrow ⟹ A = d , B = a 1 − d A=d,B=a_1-d A=d,B=a1−d
求和公式: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn ⟹ \Longrightarrow ⟹ C = d 2 , D = a 1 − d 2 C=\frac{d}{2},D=a_1-\frac{d}{2} C=2d,D=a1−2d
所以记住, A = d , B = a 1 − d , C = d 2 , D = a 1 − d 2 ,验证: A + B = C + D A=d,B=a_1-d,C=\frac{d}{2},D=a_1-\frac{d}{2},验证:A+B=C+D A=d,B=a1−d,C=2d,D=a1−2d,验证:A+B=C+D】
【递推数列
⟹ \Longrightarrow ⟹类等差数列 ⟹ \Longrightarrow ⟹累加法 ⟹ \Longrightarrow ⟹形如 a n + 1 = a n + f ( n ) 或 a n + 1 − a n = f ( n ) a_{n+1}=a_n+f(n)或a_{n+1}-a_n=f(n) an+1=an+f(n)或an+1−an=f(n) ⟹ \Longrightarrow ⟹写出若干项,再相加求解。
⟹ \Longrightarrow ⟹类等比数列 ⟹ \Longrightarrow ⟹累乘法 ⟹ \Longrightarrow ⟹ a n + 1 = a n ⋅ f ( n ) 或 a n + 1 a n = f ( n ) a_{n+1}=a_n·f(n)或\frac{a_{n+1}}{a_n}=f(n) an+1=an⋅f(n)或anan+1=f(n) ⟹ \Longrightarrow ⟹写出若干项,再相乘求解。
⟹ \Longrightarrow ⟹构造等差数列 ⟹ \Longrightarrow ⟹满足 b n + 1 − b n = 常数 b_{n+1}-b_n=常数 bn+1−bn=常数 ⟹ \Longrightarrow ⟹结论1:当看到 a n + 1 = a n c a n + 1 a_{n+1}=\frac{a_n}{ca_n+1} an+1=can+1an,那么{ 1 a n \frac{1}{a_n} an1}为等差数列;结论2:当看到 a n + 1 = q a n + q n a_{n+1}=qa_n+q^n an+1=qan+qn,两边同时除以 q n + 1 q^{n+1} qn+1来构造等差数列。
⟹ \Longrightarrow ⟹构造等比数列 ⟹ \Longrightarrow ⟹满足 b n + 1 b n = 常数 \frac{b_{n+1}}{b_n}=常数 bnbn+1=常数 ⟹ \Longrightarrow ⟹结论1:当看到 a n + 1 = q a n + c a_{n+1}= qa_n+c an+1=qan+c时,转化为 a n + 1 + k = q ( a n + k ) a_{n+1}+k=q(a_n+k) an+1+k=q(an+k),其中 k = c q − 1 k=\frac{c}{q-1} k=q−1c,构造等比数列即可。或者,类一次函数, a n + 1 = A ⋅ a n + B a_{n+1}=A·a_n+B an+1=A⋅an+B,构造等比数法, b n = a n + B A − 1 b_n=a_n+\frac{B}{A-1} bn=an+A−1B。结论2:当看到 a n + 1 = A a n + B n + C a_{n+1}=Aa_n+Bn+C an+1=Aan+Bn+C型,可化成 a n + 1 + p ( n + 1 ) + q = A ( a n + p n + q ) a_{n+1}+p(n+1)+q=A(a_n+pn+q) an+1+p(n+1)+q=A(an+pn+q)的形式来求通项。
⟹ \Longrightarrow ⟹没上述特点,列举前面若干项,寻找规律】
文章目录
- 数列
- 2023
- 2022
- 真题(2022-19)-代数-数列-等比数列-出现“三个数”-等比中项;-几何-平面几何
- 真题(2022-21)-代数-数列-等比数列-出现“三个数”,用等比中项- a c = b 2 ac=b^2 ac=b2;-代数-几何-平面几何-三角形-勾股定理
- 真题(2022-23)-代数-数列-等比数列-出现“三个数”,用等比中项;+代数-函数-一元二次函数
- 真题(2022-24)-代数-数列-等差数列-判定等差数列:①定义法: a n − a n − 1 = d a_n-a_{n-1}=d an−an−1=d;②通项形如 a n = A n + B a_n=An+B an=An+B;③前n项和形如 S n − C n 2 + D n S_n-Cn^2+Dn Sn−Cn2+Dn;-代数-数列-递推数列-形如 a n + 1 = a n + f ( n ) 或 a n + 1 − a n = f ( n ) a_{n+1}=a_n+f(n)或a_{n+1}-a_n=f(n) an+1=an+f(n)或an+1−an=f(n),称为类等差数列,可以写出若干项,再相加求解。=先写出若干项,再用累加法求解。
- 2021
- 真题(2021-02)-代数-数列-等差数列-出现“三”,用等差中项,2b=a+c;-前10题特值法、设未知数
- 真题(2021-24)-代数-数列-等比数列-等比数列判定-特征判断法-
- 真题(2021-25)-代数-数列-等差数列和等比数列;-几何-平面几何-三角形-相似;这种纯文字题,需要设未知数,但是很麻烦
- 2020
- 2019
- 真题(2019-15)-代数-数列-递推公式-构造等比数列-结论1:当看到 a n + 1 = q a n + c a_{n+1}= qa_n+c an+1=qan+c时,转化为 a n + 1 + k = q ( a n + k ) a_{n+1}+k=q(a_n+k) an+1+k=q(an+k),其中 k = c q − 1 k=\frac{c}{q-1} k=q−1c,构造等比数列即可。
- 真题(2019-16)-代数-数列-等比数列-数列的判定-
- 真题(2019-25)-代数-数列-等差数列-数列判定-特征判断法- S n S_n Sn的特征:形如一个没有常数项的一元二次函数: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn(C,D为常数)
- 2018
- 2017
- 真题(2017-03)-代数-数列-等差数列-出现“三”-等差中项-数列应用题
- 2016
- 真题(2016-24)-代数-数列-递推公式-直接计算法-举反例
- 2015
- 真题(2015-20)-E-代数-数列-等差数列
- 真题(2015-23)-代数-数列-等差数列-前n项和的最值-若 a 1 < 0 , d > 0 a_1<0,d>0 a1<0,d>0时, S n S_n Sn有最小值。
- 2014
- 真题(2014-07)-代数-数列-等差数列-出现“三”,用等差中项-
- 真题(2014-18)-代数-数列-等差数列&等比数列-既是等差数列又是等比数列的数列是非零的常数列
- 真题(2014-21)-A-代数-数列-等差数列;-方程-一元二次方程-判别式- △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
- 2013
- 真题(2013-13)-代数-数列-等差数列-下标和公式;-代数-方程-一元二次方程-韦达定理- x 1 + x 2 = − b / a x_1+x_2=-b/a x1+x2=−b/a
- 真题(2013-25)-代数-数列-递推公式-难度升级-中间段才出现周期
数列
2023
真题(2023-18)-代数-数列-等比数列-性质-递增需要 a 1 > 1 , q > 1 a_1>1,q>1 a1>1,q>1;-代数-方程-一元二次方程-根-因式分解


真题(2023-24)-代数-数列-等比数列- a n a_n an与 S n S_n Sn的关系(重要)


2022
有趣,2022年跟等比中项杠上了
真题(2022-19)-代数-数列-等比数列-出现“三个数”-等比中项;-几何-平面几何
19.在△ 𝐴𝐵𝐶 中,𝐷 为 𝐵𝐶 边上的点, 𝐵𝐷 、 𝐴𝐵 、𝐵𝐶成等比数列,则 ∠𝐵𝐴𝐶 = 90°。
(1)𝐵𝐷 = 𝐷𝐶。
(2) 𝐴𝐷 ⊥ 𝐵𝐶。

真题(2022-21)-代数-数列-等比数列-出现“三个数”,用等比中项- a c = b 2 ac=b^2 ac=b2;-代数-几何-平面几何-三角形-勾股定理
21.某直角三角形的三边长 𝑎 , 𝑏 , 𝑐 成等比数列,则能确定公比的值。
(1)𝑎 是直角边长。
(2)𝑐 是斜边长。

真题(2022-23)-代数-数列-等比数列-出现“三个数”,用等比中项;+代数-函数-一元二次函数
23.已知𝑎,𝑏为实数,则能确定𝑎的值。
(1)𝑎,𝑏,𝑎 + 𝑏成等比数列。
(2)𝑎(𝑎 + 𝑏) > 0。

真题(2022-24)-代数-数列-等差数列-判定等差数列:①定义法: a n − a n − 1 = d a_n-a_{n-1}=d an−an−1=d;②通项形如 a n = A n + B a_n=An+B an=An+B;③前n项和形如 S n − C n 2 + D n S_n-Cn^2+Dn Sn−Cn2+Dn;-代数-数列-递推数列-形如 a n + 1 = a n + f ( n ) 或 a n + 1 − a n = f ( n ) a_{n+1}=a_n+f(n)或a_{n+1}-a_n=f(n) an+1=an+f(n)或an+1−an=f(n),称为类等差数列,可以写出若干项,再相加求解。=先写出若干项,再用累加法求解。
24.已知正数列{ a n a_n an},则{ a n a_n an}是等差数列。
(1) a n + 1 2 − a n 2 = 2 n , n = 1 , 2 , . . . a_{n+1}^2-a_n^2=2n,n=1,2,... an+12−an2=2n,n=1,2,...。
(2) a 1 + a 3 = 2 a 2 a_1+a_3=2a_2 a1+a3=2a2。


2021
真题(2021-02)-代数-数列-等差数列-出现“三”,用等差中项,2b=a+c;-前10题特值法、设未知数
2.三位年轻人的年龄成等差数列,且最大与最小的两人年龄差的10倍是另一人的年龄,则三人中年龄最大的是( )。
A.19
B.20
C.21
D.22
E.23

真题(2021-24)-代数-数列-等比数列-等比数列判定-特征判断法-
24.已知数列{ a n a_n an},则数列{ a n a_n an}为等比数列。
(1) a n a n + 1 > 0 a_na_{n+1}>0 anan+1>0。
(2) a n + 1 2 − 2 a n 2 − a n a n + 1 = 0 a^2_{n+1}-2a^2_n-a_na_{n+1}=0 an+12−2an2−anan+1=0。

真题(2021-25)-代数-数列-等差数列和等比数列;-几何-平面几何-三角形-相似;这种纯文字题,需要设未知数,但是很麻烦
25.给定两个直角三角形,则这两个直角三角形相似。
(1)每个直角三角形边长成等比数列。
(2)每个直角三角形边长成等差数列。


2020
真题(2020-05)-代数-数列-等差数列-最值-等差数列的前n项和可以整理成一元二次函数的形式: S n = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2dn2+(a1−2d)n,对称轴为 n = − a 1 − d 2 2 × d 2 = 1 2 − a 1 d n=-\frac{a_1-\frac{d}{2}}{2×\frac{d}{2}}=\frac{1}{2}-\frac{a_1}{d} n=−2×2da1−2d=21−da1,最值取在最靠近对称轴的整数处。or-莫名巧合:等差数列-通项公式: a n = A n + B a_n=An+B an=An+B ⟹ \Longrightarrow ⟹ A = d , B = a 1 − d A=d,B=a_1-d A=d,B=a1−d;求和公式: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn ⟹ \Longrightarrow ⟹ C = d 2 , D = a 1 − d 2 C=\frac{d}{2},D=a_1-\frac{d}{2} C=2d,D=a1−2d,所以记住, A = d , B = a 1 − d , C = d 2 , D = a 1 − d 2 ,验证: A + B = C + D A=d,B=a_1-d,C=\frac{d}{2},D=a_1-\frac{d}{2},验证:A+B=C+D A=d,B=a1−d,C=2d,D=a1−2d,验证:A+B=C+D
5、若等差数列{ a n a_n an} 满足 a 1 = 8 a_1=8 a1=8,且 a 2 + a 4 = a 1 a_2+a_4=a_1 a2+a4=a1,则{ a n a_n an} 的前n 项和的最大值为( )
A.16
B.17
C.18
D.19
E.20


最值:
1.等差数列前n项和 S n S_n Sn有最值的条件
(1)若 a 1 < 0 , d > 0 a_1<0,d>0 a1<0,d>0时, S n S_n Sn有最小值。
(2)若 a 1 > 0 , d < 0 a_1>0,d<0 a1>0,d<0时, S n S_n Sn有最大值。
2.求解等差数列 S n S_n Sn最值的方法
(1)一元二次函数法
等差数列的前n项和可以整理成一元二次函数的形式: S n = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2dn2+(a1−2d)n,对称轴为 n = − a 1 − d 2 2 × d 2 = 1 2 − a 1 d n=-\frac{a_1-\frac{d}{2}}{2×\frac{d}{2}}=\frac{1}{2}-\frac{a_1}{d} n=−2×2da1−2d=21−da1,最值取在最靠近对称轴的整数处。
特别地,若 S m = S n S_m=S_n Sm=Sn,即 S m + n = 0 S_{m+n}=0 Sm+n=0时,对称轴为 m + n 2 \frac{m+n}{2} 2m+n。
(2) a n = 0 a_n=0 an=0法
最值一定在“变号”时取得,可令a=0,则有
① 若解得n为整数,则 S n = S n − 1 S_n=S_{n-1} Sn=Sn−1均为最值。例如,若解得n=6,则 S 6 = S 5 S_6=S_5 S6=S5为其最值。
② 若解得n为非整数,则当n取其整数部分m(m=[n])时, S m S_m Sm取到最值。例如,若解得n=6.9,则 S 6 S_6 S6为其最值。
真题(2020-11)-代数-数列-递推数列-没特点,列举若干项,找周期;类等差数列,累加法;类等比数列,累乘法。
11、已知数列{ a n a_n an}满足 a 1 = 1 a_1=1 a1=1, a 2 = 2 a_2=2 a2=2,且 a n + 2 = a n + 1 − a n ( n = 1 , 2 , 3 , . . . ) a_{n+2}=a_{n+1}-a_n(n=1,2,3,...) an+2=an+1−an(n=1,2,3,...),则 a 100 a_{100} a100=( )
A.1
B.-1
C.2
D.-2
E.0


2019
真题(2019-15)-代数-数列-递推公式-构造等比数列-结论1:当看到 a n + 1 = q a n + c a_{n+1}= qa_n+c an+1=qan+c时,转化为 a n + 1 + k = q ( a n + k ) a_{n+1}+k=q(a_n+k) an+1+k=q(an+k),其中 k = c q − 1 k=\frac{c}{q-1} k=q−1c,构造等比数列即可。
-秒杀:复杂选项(选多法):复杂选项可秒杀,按多的选(选多法),选项哪些因素出现多,就选哪些(90%准确率)1、99多,排除选项DE;2、-1,+1多,排除选项B。结果只能是A,C。看题干a1=0,C任何情况的不为0,所以选A。
15、设数列{ a n {a_n} an}满足 a 1 = 0 , a n + 1 − 2 a n = 1 a_1=0,a_{n+1}-2a_n=1 a1=0,an+1−2an=1,则 a 100 = a_{100}= a100=()
A. 2 99 − 1 2^{99}-1 299−1
B. 2 99 2^{99} 299
C. 2 99 + 1 2^{99}+1 299+1
D. 2 100 − 1 2^{100}-1 2100−1
E. 2 100 + 1 2^{100}+1 2100+1


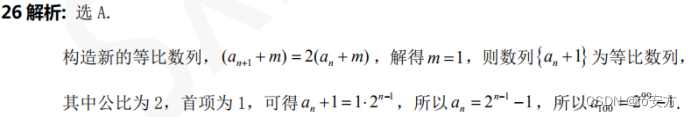
秒杀:复杂选项(选多法):复杂选项可秒杀,按多的选(选多法),选项哪些因素出现多,就选哪些(90%准确率)1、99多,排除选项DE;2、-1,+1多,排除选项B。结果只能是A,C。看题干a1=0,C任何情况的不为0,所以选A。
真题(2019-16)-代数-数列-等比数列-数列的判定-
16、甲、乙、丙三人各自拥有不超过10本图书,甲再购入2本图书后,他们拥有的图书量构成等比数列,则能确定甲拥有图书的数量。
(1) 已知乙拥有的图书数量。
(2) 已知丙拥有的图书数量。


真题(2019-25)-代数-数列-等差数列-数列判定-特征判断法- S n S_n Sn的特征:形如一个没有常数项的一元二次函数: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn(C,D为常数)
25、设数列{ a n a_n an}的前n项和为 S n S_n Sn,则{ a n a_n an}等差。
(1) S n = n 2 + 2 n , n = 1 , 2 , 3 S_n=n^2+2n,n=1,2,3 Sn=n2+2n,n=1,2,3。
(2) S n = n + 2 n + 1 , n = 1 , 2 , 3 S_n=n^+2n+1,n=1,2,3 Sn=n+2n+1,n=1,2,3。


2018
真题(2018-07)-代数-数列-等比数列-无穷等比数列
7.四边形 A 1 B 1 C 1 D 1 A_1B_1C_1D_1 A1B1C1D1是平行四边形, A 2 B 2 C 2 D 2 A_2B_2C_2D_2 A2B2C2D2是 A 1 B 1 C 1 D 1 A_1B_1C_1D_1 A1B1C1D1四边的中点, A 3 B 3 C 3 D 3 A_3B_3C_3D_3 A3B3C3D3分别是 A 2 B 2 C 2 D 2 A_2B_2C_2D_2 A2B2C2D2四边中点,依次下去,得到四边形序列 A n B n C n D n A_nB_nC_nD_n AnBnCnDn(n = 1、2、3…) ,设 A n B n C n D n A_nB_nC_nD_n AnBnCnDn面积为 S n S_n Sn,且 S 1 = 12 S_1=12 S1=12,则 S 1 + S 2 + S 3 + . . . = () S_1+S_2+S_3+...=() S1+S2+S3+...=()
A. 16 16 16
B. 20 20 20
C. 24 24 24
D. 28 28 28
E. 30 30 30
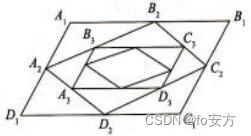




真题(2018-17)-B-代数-数列-等差数列-求和公式: S n = n ( a 1 + a n ) 2 = n a n + 1 2 ( n 为偶数时,可虚拟小数) = n a 1 + n ( n − 1 ) 2 d = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{n(a_1+a_n)}{2}=na_{\frac{n+1}{2}}(n为偶数时,可虚拟小数)=na_1+\frac{n(n-1)}{2}d=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2n(a1+an)=na2n+1(n为偶数时,可虚拟小数)=na1+2n(n−1)d=2dn2+(a1−2d)n
17.{ a n a_n an}等差数列,则能确定 a 1 + a 2 + . . . + a 9 a_1+a_2+...+a_9 a1+a2+...+a9的值。
(1)已知 a 1 a_1 a1的值。
(2)已知 a 5 a_5 a5的值。



2017
真题(2017-03)-代数-数列-等差数列-出现“三”-等差中项-数列应用题
3.甲、乙、丙三种货车载重量成等差数列,2 辆甲种车和 1 辆乙种车的满载量为 95 吨,1辆甲种车和 3 辆丙种车载重量为 150 吨,则用甲、乙、丙各一辆车一次最多运送货物为( )吨。
A.125
B.120
C.115
D.110
E.105


2016
真题(2016-24)-代数-数列-递推公式-直接计算法-举反例
24.已知数列 a 1 , a 2 , a 3 , . . . , a 10 a_1,a_2,a_3,...,a_{10} a1,a2,a3,...,a10,则 a 1 − a 2 + a 3 − . . . + a 9 − a 10 ≥ 0 a_1-a_2+a_3-...+a_9-a_{10}≥0 a1−a2+a3−...+a9−a10≥0
(1) a n ≥ a n + 1 , n = 1 , 2 , . . . , 9 a_n≥a_{n+1},n=1,2,...,9 an≥an+1,n=1,2,...,9
(2) a n 2 ≥ a n + 1 2 , n = 1 , 2 , . . . , 9 a_n^2≥a_{n+1}^2,n=1,2,...,9 an2≥an+12,n=1,2,...,9

2015
真题(2015-20)-E-代数-数列-等差数列
20.设{ a n a_n an}是等差数列,则能确定数列{ a n a_n an}。
(1) a 1 + a 6 = 0 a_1+a_6=0 a1+a6=0
(2) a 1 a 6 = − 1 a_1a_6=-1 a1a6=−1

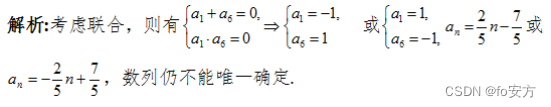
真题(2015-23)-代数-数列-等差数列-前n项和的最值-若 a 1 < 0 , d > 0 a_1<0,d>0 a1<0,d>0时, S n S_n Sn有最小值。
23.已知数列{ a n a_n an}是公差大于零的等差数列,{ S n S_n Sn}是{ a n a_n an}的前n 项和。则 S n ≥ S 10 , n = 1 , 2 , . . . S_n≥S_{10},n=1,2,... Sn≥S10,n=1,2,...
(1) a 10 = 0 a_{10}=0 a10=0
(2) a 11 a 10 < 0 a_{11}a_{10}<0 a11a10<0



2014
真题(2014-07)-代数-数列-等差数列-出现“三”,用等差中项-
7.已知{ a n a_n an}为等差数列,且 a 2 − a 5 + a 8 = 9 a_2-a_5+a_8=9 a2−a5+a8=9 ,则 a 1 + a 2 + . . . + a 9 = () a_1+a_2+...+a_9=( ) a1+a2+...+a9=()
A.27
B.45
C.54
D.81
E.182
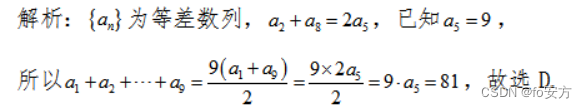

真题(2014-18)-代数-数列-等差数列&等比数列-既是等差数列又是等比数列的数列是非零的常数列
18.甲、乙、丙三人的年龄相同
(1)甲、乙、丙的年龄成等差数列
(2)甲、乙、丙的年龄成等比数列


真题(2014-21)-A-代数-数列-等差数列;-方程-一元二次方程-判别式- △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
21.方程 x 2 + 2 ( a + b ) x + c 2 = 0 x^2+2(a+b)x+c^2=0 x2+2(a+b)x+c2=0 有实根。
(1) a, b, c 是一个三角形的三边长。
(2)实数a, b, c 成等差数列。


2013
真题(2013-13)-代数-数列-等差数列-下标和公式;-代数-方程-一元二次方程-韦达定理- x 1 + x 2 = − b / a x_1+x_2=-b/a x1+x2=−b/a
13.已知{ a n a_n an}为等差数列,若 a 2 a_2 a2和 a 10 a_{10} a10是方程 x 2 − 10 x − 9 = 0 x^2-10x-9=0 x2−10x−9=0的两个根,则 a 5 + a 7 = a_5+a_7= a5+a7=( )。
A. − 10 -10 −10
B. − 9 -9 −9
C. 9 9 9
D. 10 10 10
E. 12 12 12

真题(2013-25)-代数-数列-递推公式-难度升级-中间段才出现周期
25.设 a 1 = 1 , a 2 = k , . . . , a n + 1 = ∣ a n − a n − 1 ∣ , ( n ≥ 2 ) a_1=1,a_2=k,...,a_{n+1}=|a_n-a_{n-1}|,(n≥2) a1=1,a2=k,...,an+1=∣an−an−1∣,(n≥2) ,则 a 100 + a 101 + a 102 = 2 a_{100}+a_{101}+a_{102}=2 a100+a101+a102=2
(1) k = 2 k = 2 k=2
(2)k 是小于 20 的正整数







![如何预防[[MyFile@waifu.club]].wis [[backup@waifu.club]].wis勒索病毒感染您的计算机?](https://img-blog.csdnimg.cn/direct/7469270cadcc4d8894498d858b805957.png)