图像基本运算
一、实验内容:
1. 熟悉和掌握利用Matlab工具进行数字图像的读、写、显示等数字图像处理基本步骤。
2. 熟练掌握各种图像点运算的基本原理及方法。
3. 能够从深刻理解点运算,并能够思考拓展到一定的应用领域。
二、实验原理:
1、单幅图像像素灰度的点运算;
2、两幅图像的代数与逻辑运算;
3、单幅图像缩放与旋转的几何变换。
三、实验方法及程序
1、点运算
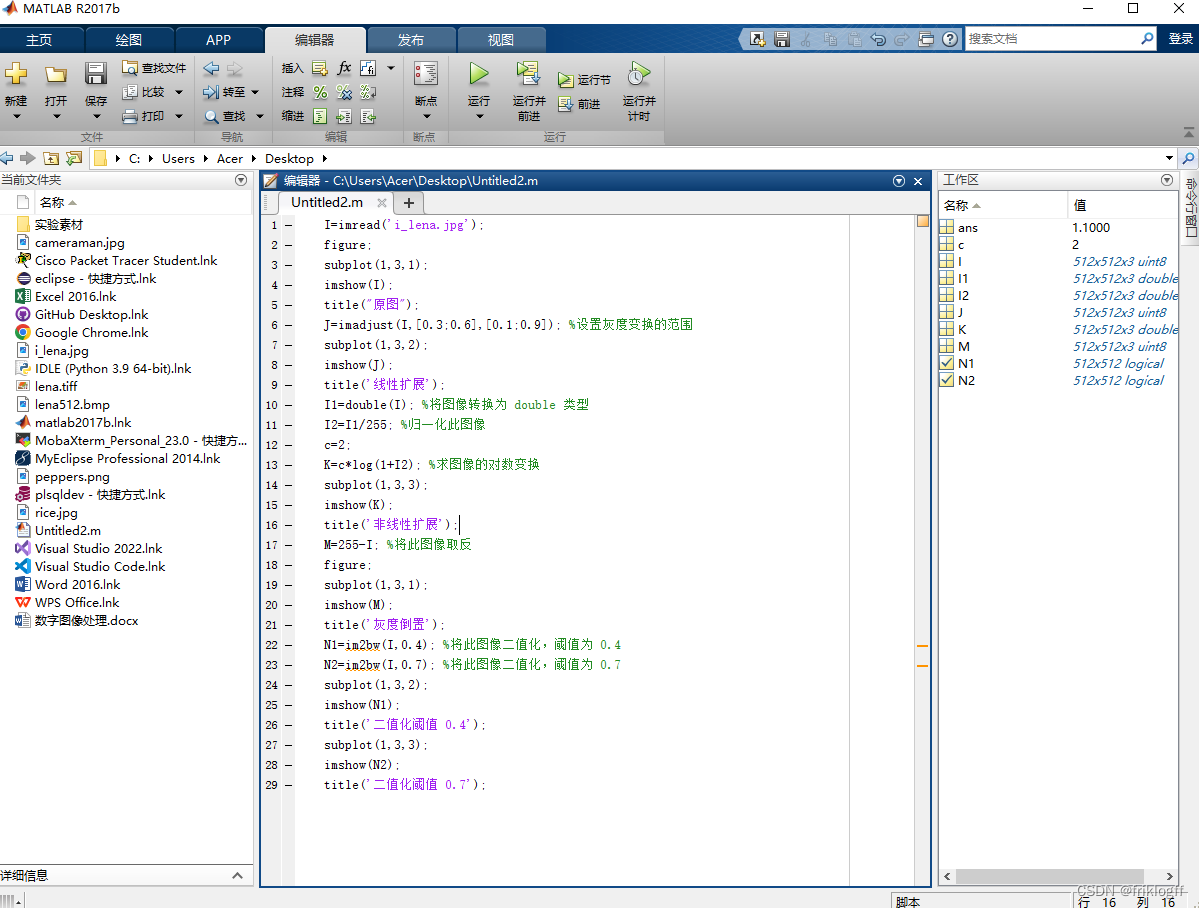
(1)选择一幅图像 lena.jpg,设置输入/输出变换的灰度级范围,a=0.3, b=0.6,c=0.1,d=0.9。
(2)设置非线性扩展函数的参数 c=2。
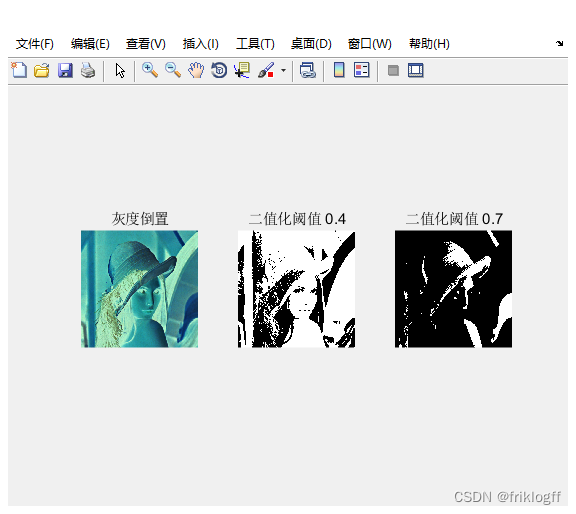
(3)采用灰度倒置变换函数 s 255 r 进行图像变换。
(4)设置二值化图像的阈值,分别为 level=0.4,level=0.7 参考程序如下:
2、图像代数、逻辑运
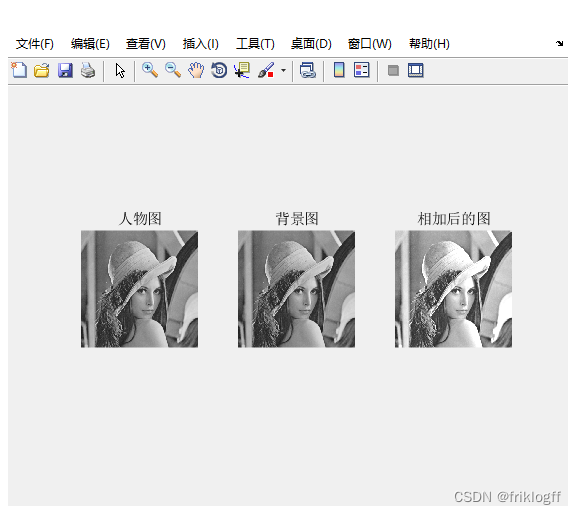
(1)选取两幅大小一样的灰度图像 i_lena.jpg 和 rice.png,将两幅图像 进行加法运算。程序如下所示:

(2)选取一幅混合图像,如(1)相加得到的图像 i_lena.jpg,将混合图 像与背景图像做减法运算,程序如下所示:

3、图像几何变换
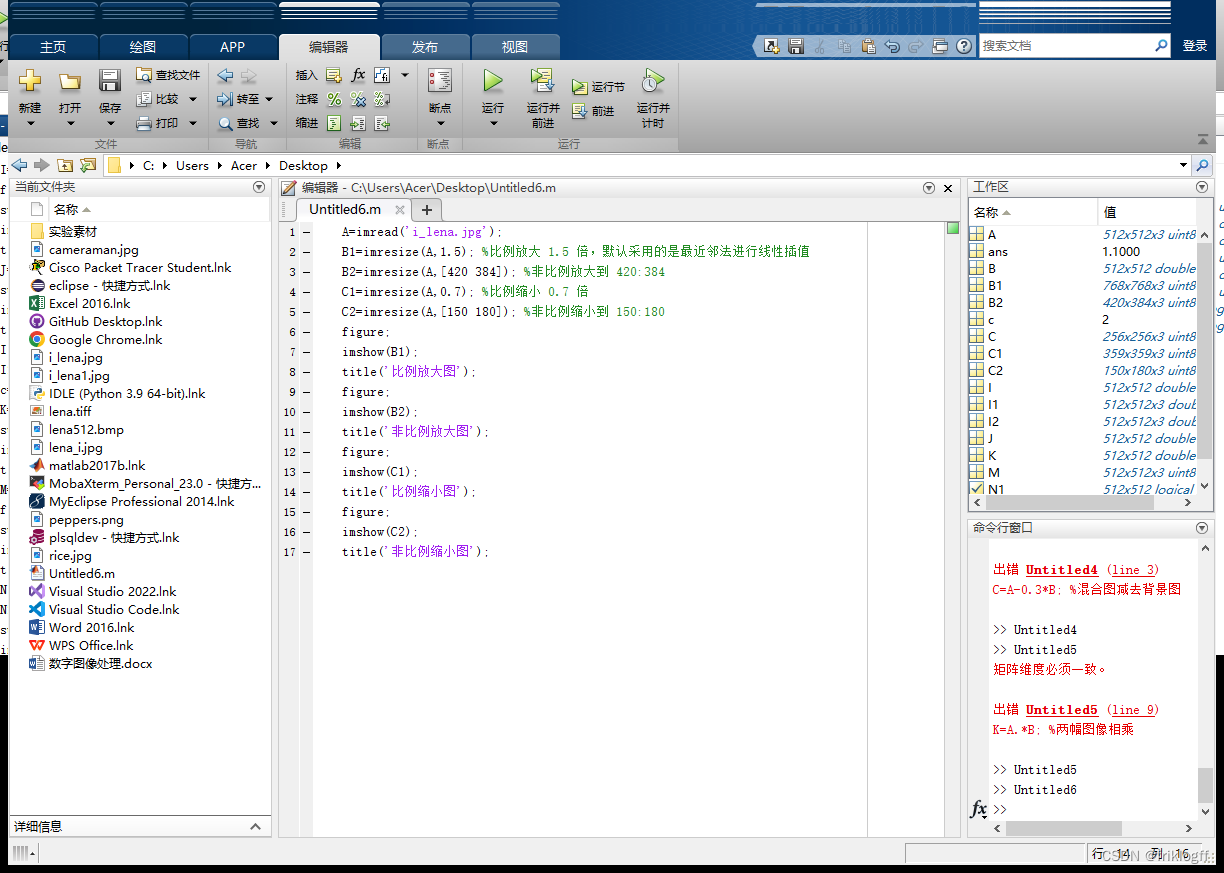
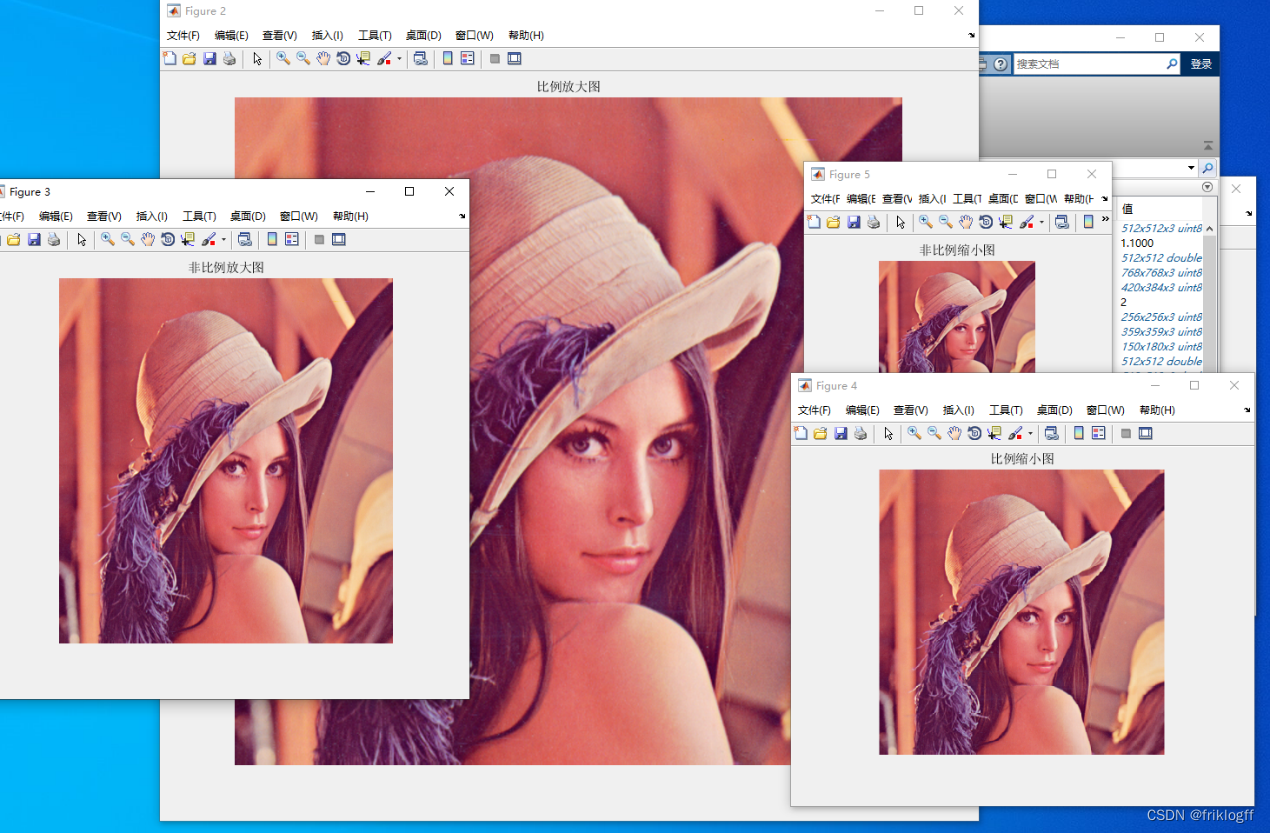
(1)选取一幅大小为256256像素的图像,如 i_lena.jpg.分别将图比例放大 1.5 倍,比例缩小 0.7 倍,非比例放大到420384像素,非比例缩小到150180像素。 程序如下所示:
(2)读取一幅图片,如 i_lena.jpg,设置图像旋转的角度分别为 0 45 和 0 90 ,采用 图形旋转函数 imrotate 对图像进行旋转。程序如下所示
五、实验结果分析
1、点运算

2、图像代数、逻辑运
(1)
(2)

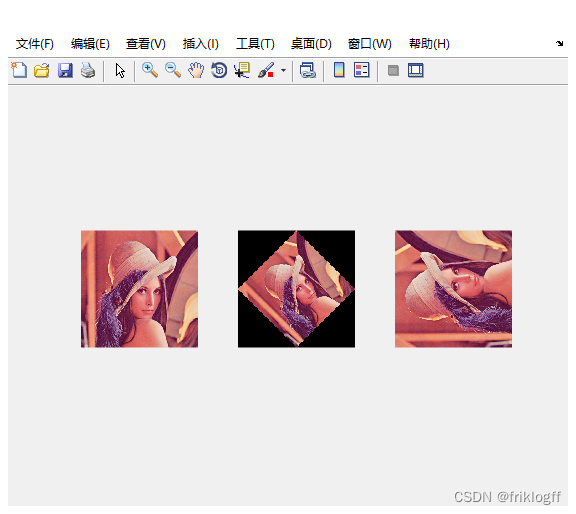
3、图像几何变换
(1)
(2)
六、思考题
1.线性扩展与对数非线性扩展各有什么特点?对数非线性交换能否使图像的低灰度级压缩,高灰度级扩展或者低灰度级扩展,高灰度级压缩?
答:
线性扩展:简单地通过线性变换扩展图像的灰度级,适用于整体对比度较低的图像。
对数非线性扩展:强调低灰度级的细节,对高灰度级进行压缩,适用于增强图像细节的同时压缩高亮区域,使图像更具视觉效果。
对数非线性扩展可以实现:
- 低灰度级压缩,使低灰度级区域更加黑暗。
- 高灰度级扩展,增强图像的高亮部分。
2.任意两幅图片相叠加得到一幅混合图像,将此混合图像减去其中的一幅原图 像能得到另一幅原图像吗?通过以上实验小结各种图像代数运算的应用特点。
答:
图像相叠加得到混合图像,减去其中一幅原图像可以得到另一幅原图像。
图像代数运算(加法、减法)可用于图像融合、增强和还原。
3.由非比例缩放得到的图片能够恢复到原图片吗?为什么?
答:
由非比例缩放得到的图片通常不能完全恢复到原图片。
非比例缩放引入了信息的丢失,导致不能准确还原原始图像。
4.图像的旋转会导致图像的失真吗?若有,有什么办法可以解决这个问题?
答:
旋转可能导致图像失真,尤其是在角度较大时。
使用插值算法(如双线性插值)可以在旋转过程中减少失真,但在大角度旋转时,还是可能引入一定程度的失真。