算法leetcode｜94. 二叉树的中序遍历（多语言实现）

文章目录

94. 二叉树的中序遍历：
- 样例 1：
- 样例 2：
- 样例 3：
- 提示：
分析：
题解：
- rust：
- go：
- c++：
- python：
- java：

94. 二叉树的中序遍历：

给定一个二叉树的根节点 root ，返回它的中序遍历。

样例 1：

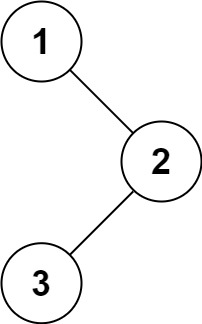
输入：root = [1,null,2,3]输出：[1,3,2]

样例 2：

输入：root = []输出：[]

样例 3：

输入：root = [1]输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

分析：

面对这道算法题目，二当家的再次陷入了沉思。
二叉树的中序遍历和前序遍历，后续遍历是二叉树常用的遍历方式。
使用递归方式比循环非递归方式更加简单，直观，易于理解。
通常二叉树的中序遍历一定要使用一个栈结构，因为中序遍历的要求是遍历完左子树才能遍历当前节点，但是遍历到了左子树就无法再回到当前节点了，所以一般都是使用压栈的方式，先将当前节点压栈，遍历完左子树再将当前节点出栈，这样空间复杂度就会是 O(n) （递归也相当于使用了栈结构）。
说起来这不是什么大问题，但是算法就是要想办法优化降低时间和空间的复杂度，于是寄出一种可以将空间复杂度降低为 O(1) 的中序遍历方式，Morris 中序遍历。
事实上Morris 中序遍历不是没有代价的，由于要做额外的节点连接和恢复，相当于用时间换空间。

题解：

rust：

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {pub fn inorder_traversal(mut root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {let mut ans = Vec::new();while root != None {if root.as_ref().unwrap().borrow().left != None {// 寻找当前 root 节点的前驱节点：前驱 predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止let mut predecessor = root.as_ref().unwrap().borrow().left.clone();while predecessor.as_ref().unwrap().borrow().right != None&& predecessor.as_ref().unwrap().borrow().right != root {predecessor = predecessor.unwrap().borrow().right.clone();}if predecessor.as_ref().unwrap().borrow().right == None {// 让前驱 predecessor 节点的右指针指向当前 root 节点，继续遍历左子树，之后会再次回到当前 root 节点predecessor.unwrap().borrow_mut().right = root.clone();// 遍历左子树root = root.unwrap().borrow().left.clone();continue;} else {// 左子树遍历完毕又回到了当前 root 节点，让前驱 predecessor 节点的右指针与当前 root 节点断开，恢复原样predecessor.unwrap().borrow_mut().right = None;}}// 遍历当前 root 节点ans.push(root.as_ref().unwrap().borrow().val);// 遍历当前 root 节点的右子树root = root.unwrap().borrow().right.clone();}return ans;}
}

go：

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func inorderTraversal(root *TreeNode) []int {var ans []intfor root != nil {if root.Left != nil {// 寻找当前 root 节点的前驱节点：前驱 predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止predecessor := root.Leftfor predecessor.Right != nil && predecessor.Right != root {// 有右子树且没有设置过指向 root，则继续向右走predecessor = predecessor.Right}if predecessor.Right == nil {// 让前驱 predecessor 节点的右指针指向当前 root 节点，继续遍历左子树，之后会再次回到当前 root 节点predecessor.Right = root// 遍历左子树root = root.Leftcontinue} else {// 左子树遍历完毕又回到了当前 root 节点，让前驱 predecessor 节点的右指针与当前 root 节点断开，恢复原样predecessor.Right = nil}}// 遍历当前 root 节点ans = append(ans, root.Val)// 遍历当前 root 节点的右子树root = root.Right}return ans
}

c++：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> ans;while (root != nullptr) {if (root->left != nullptr) {// 寻找当前 root 节点的前驱节点：前驱 predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止TreeNode *predecessor = root->left;while (predecessor->right != nullptr && predecessor->right != root) {predecessor = predecessor->right;}if (predecessor->right == nullptr) {// 让前驱 predecessor 节点的右指针指向当前 root 节点，继续遍历左子树，之后会再次回到当前 root 节点predecessor->right = root;// 遍历左子树root = root->left;continue;} else {// 左子树遍历完毕又回到了当前 root 节点，让前驱 predecessor 节点的右指针与当前 root 节点断开，恢复原样predecessor->right = nullptr;}}// 遍历当前 root 节点ans.emplace_back(root->val);// 遍历当前 root 节点的右子树root = root->right;}return ans;}
};

python：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:ans = list()while root is not None:if root.left is not None:# 寻找当前 root 节点的前驱节点：前驱 predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止predecessor = root.leftwhile predecessor.right is not None and predecessor.right != root:# 有右子树且没有设置过指向 root，则继续向右走predecessor = predecessor.rightif predecessor.right is None:# 让前驱 predecessor 节点的右指针指向当前 root 节点，继续遍历左子树，之后会再次回到当前 root 节点predecessor.right = root# 遍历左子树root = root.leftcontinueelse:# 左子树遍历完毕又回到了当前 root 节点，让前驱 predecessor 节点的右指针与当前 root 节点断开，恢复原样predecessor.right = None# 遍历当前 root 节点ans.append(root.val)# 遍历当前 root 节点的右子树root = root.rightreturn ans

java：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<Integer>();while (root != null) {if (root.left != null) {// 寻找当前 root 节点的前驱节点：前驱 predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止TreeNode predecessor = root.left;while (predecessor.right != null && predecessor.right != root) {predecessor = predecessor.right;}if (predecessor.right == null) {// 让前驱 predecessor 节点的右指针指向当前 root 节点，继续遍历左子树，之后会再次回到当前 root 节点predecessor.right = root;// 遍历左子树root = root.left;continue;} else {// 左子树遍历完毕又回到了当前 root 节点，让前驱 predecessor 节点的右指针与当前 root 节点断开，恢复原样predecessor.right = null;}}// 遍历当前 root 节点ans.add(root.val);// 遍历当前 root 节点的右子树root = root.right;}return ans;}
}