逻辑回归案例

假设表示

基于上述情况，要使分类器的输出在[0,1]之间，可以采用假设表示的方法。
设$h_{\theta }(x)=g({\theta }^{T}x)$，
其中$g(z)=\frac{1}{(1+e^{-z})}$, 称为逻辑函数（Sigmoid function，又称为激活函数，生物学上的S型曲线）
$$h_{\theta }(x)=\frac{1}{(1+e^{-{\theta }^{T}X})}$$

其两条渐近线分别为h(x)=0和h(x)=1

在分类条件下，最终的输出结果是：
$$h_{\theta }(x)=P(y=1│x,\theta )$$

其代表在给定x的条件下 其y=1的概率

$$P(y=1│x,\theta )+P(y=0│x,\theta )=1$$

决策边界（ Decision boundary）

对假设函数设定阈值$h(x)=0.5$，
当$h(x)\ge 0.5$ 时，输出结果y=1.

根据假设函数的性质，当 $x\ge 0时，$h(x)≥0.5
用${\theta }^{T}x$替换x，则当${\theta }^{T}x\ge 0$时，$h(x)\ge 0.5，y=1$

解出 ${\theta }^{T}x\ge 0$，其答案将会是一个在每一个$x_i$轴上都有的不等式函数。

这个不等式函数将整个空间分成了y=1 和 y=0的两个部分，称之为决策边界。

激活函数的代价函数

在线性回归中的代价函数：
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

令$Cost（h\theta (x)，y）=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$，
Cost是一个非凹函数，有许多的局部最小值，不利于使用梯度下降法。对于分类算法，设置其代价函数为：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})\ast log(1-h_{\theta }(x^{(i)}))]$$

对其化简：
$$Cost（h_{\theta }(x),y）=-ylog(h_{\theta }(x))-((1-y)log(1-h_{\theta }(x)))$$
检验：
当 $y=1$时，$-log(h_{\theta }(x))$
当 $y=0$时，$-log(1-h_{\theta }(x))$

那么代价函数可以写成：
$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$

对于代价函数，采用梯度下降算法求θ的最小值：
$${\theta }_j:={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}$$
代入梯度：
$${\theta }_j:={\theta }_j-\alpha \sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^i$$

sklearn 代码

导入库

##  基础函数库
import numpy as np ## 导入画图库
import matplotlib.pyplot as plt## 导入逻辑回归模型函数
from sklearn.linear_model import LogisticRegression

模型训练

## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])## 调用逻辑回归模型
lr_clf = LogisticRegression()## 用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2

模型参数查看

## 查看其对应模型的w
print('the weight of Logistic Regression:',lr_clf.coef_)## 查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)

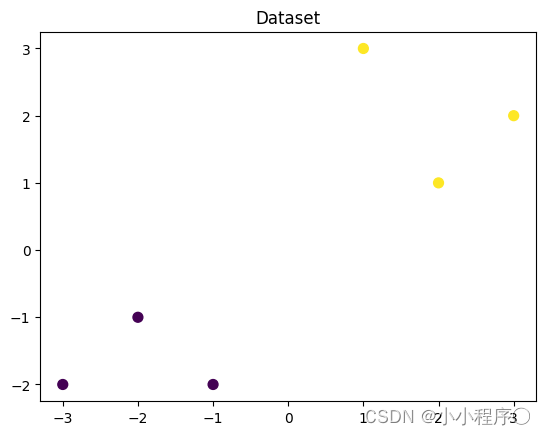
可视化构造的数据样本点

plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()

模型预测

## 在训练集和测试集上分别利用训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1)
y_label_new2_predict = lr_clf.predict(x_fearures_new2)print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)## 由于逻辑回归模型是概率预测模型（前文介绍的 p = p(y=1|x,\theta)）,所以我们可以利用 predict_proba 函数预测其概率
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)