谨以此博客作为复习期间的记录。

软间隔思想的由来

在上一篇博客中，回顾了线性可分的支持向量机,但在实际情况中，很少有完全线性可分的情况，大部分线性可分的情况都是整体线性可分，个别样本点无法线性分割开。因此就要避免这极个别样本点对分割平面产生的影响。
线性可分支持向量机

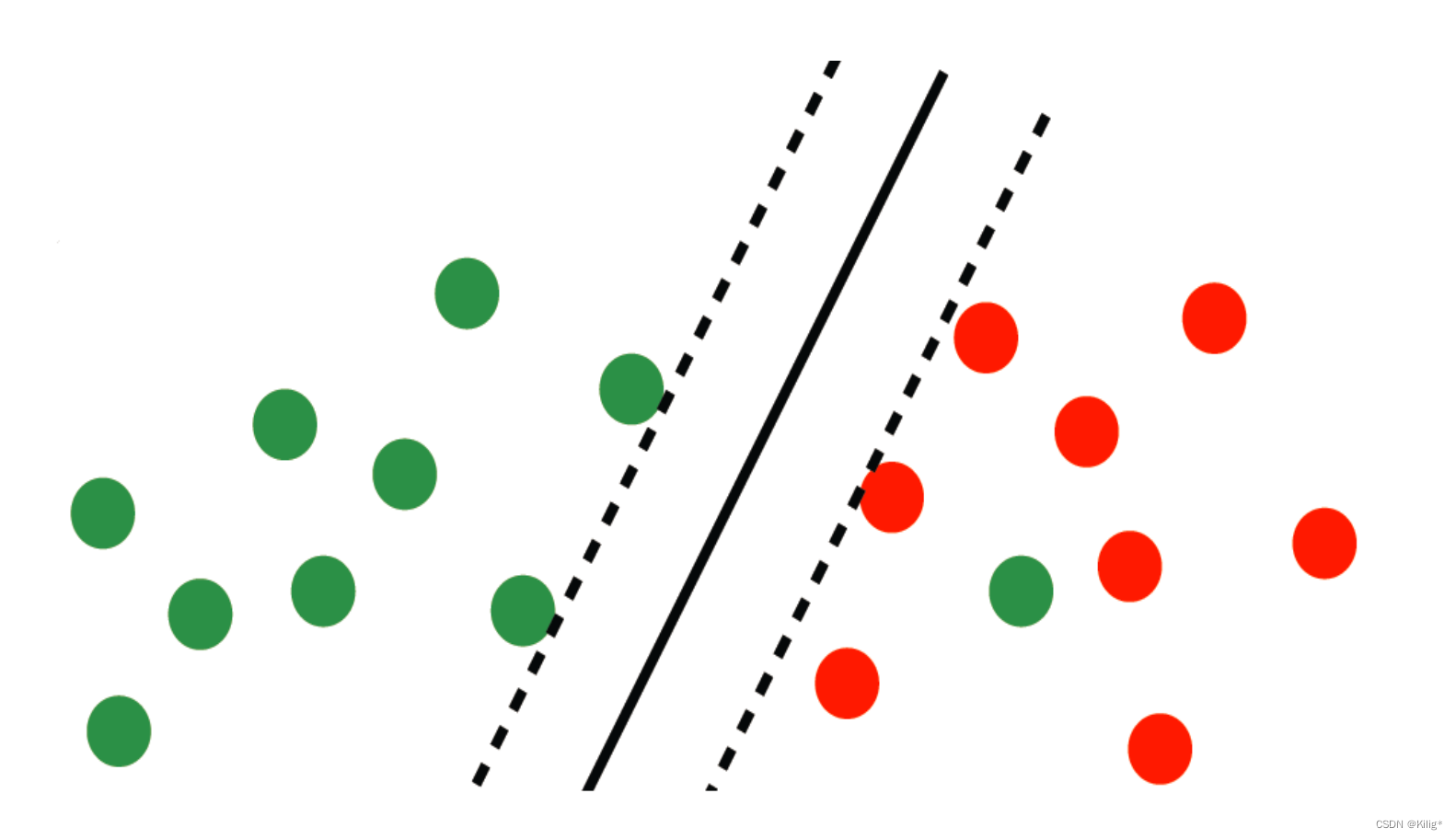
软间隔的引入

在分类过程中，允许极个别数据点“越界”，如何在目标函数中体现这一点呢？
软间隔支持向量机（Soft Margin Support Vector Machine）的数学形式可以通过修改支持向量机（SVM）的优化目标函数和约束条件来实现。软间隔允许一些数据点越界，引入了松弛变量来处理这些点。

首先，我们考虑软间隔的目标函数和约束条件：

1. 目标函数：
   最小化目标函数，同时考虑间隔的最大化和误分类点的惩罚，即：
   $$\underset{\mathbf{w},b,\mathbf{\xi }}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^N{\xi }_i$$
   这里 $\mathbf{w}$ 是超平面的法向量，$b$ 是截距，$\mathbf{\xi }$ 是松弛变量，$C>0$ 是一个超参数，用于控制对误分类点的惩罚程度。

2. 约束条件：
   考虑函数间隔大于等于 1 的约束条件，以及松弛变量 $\mathbf{\xi }$ 的非负性约束：
   $$\begin{array}{rl}& y_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)\ge 1-{\xi }_i,i=1,2,\dots ,N\\ & {\xi }_i\ge 0,i=1,2,\dots ,N\end{array}$$

线性支持向量机学习算法
输入: 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_N, y_N\right)\right\} T={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}, 其中, $x_i\in \mathcal{X}={\mathbf{R}}^n,y_i\in$ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N \mathcal{Y}=\{-1,+1\}, \quad i=1,2, \cdots, N Y={−1,+1},i=1,2,⋯,N;
输出: 分离超平面和分类决策函数.
(1) 选择惩罚参数 $C>0$, 构造并求解凸二次规划问题
$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ \text{ s.t. }& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0⩽{\alpha }_i⩽C,i=1,2,\cdots ,N\end{array}$$

求得最优解 ${\alpha }^{\ast }={\left({\alpha }_1{}^{\ast },{\alpha }_2{}^{\ast },\cdots ,{\alpha }_N{}^{\ast }\right)}^{\mathrm{T}}$.
(2) 计算 $w^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$

选择 ${\alpha }^{\ast }$ 的一个分量 ${\alpha }_j{}^{\ast }$ 适合条件 $0<{\alpha }_j^{\ast }<C$, 计算
$$b^{\ast }=y_j-\sum _{i=1}^N{y}_i{\alpha }_i^{\ast }\left(x_i\cdot x_j\right)$$
(3) 求得分离超平面
$$w^{\ast }\cdot x+b^{\ast }=0$$

分类决策函数:
$$f(x)=\mathrm{sign}\left(w^{\ast }\cdot x+b^{\ast }\right)$$