原理
傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。
定义:给定一个函数 f(t),傅立叶变换将这个函数从时域(时间域)转换到频域(频率域)上的函数 。傅立叶变换的数学表示如下:
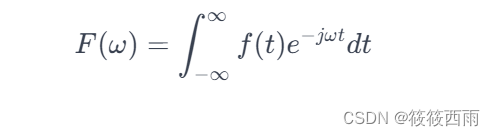
在这个表示中,F(ω) 表示频域上的复数函数,f(t) 表示时域上的函数,ω 表示频率,j 表示虚数单位。这个公式描述了将时域信号 f(t) 转换为频域信号 F(ω) 的过程。
原理:
复指数函数:傅立叶变换的核心是复指数函数ω,它表示在不同频率上的正弦和余弦振荡。傅立叶变换实际上是将信号分解为不同频率的复振幅和相位。
积分:傅立叶变换中的积分操作将时域函数给定范围内的所有时间点考虑在内,以获得频率域上的表示。这表示我们考虑了信号的所有时间信息以获取频率信息。
频谱:F(ω)表示了信号在频率ω处的振幅和相位信息。频谱显示了信号中各个频率分量的重要性。
逆变换:傅立叶变换不仅可以将信号从时域转换到频域,还可以进行逆变换,将信号从频域还原回时域,这允许我们在频域上对信号进行操作后再转换回时域。
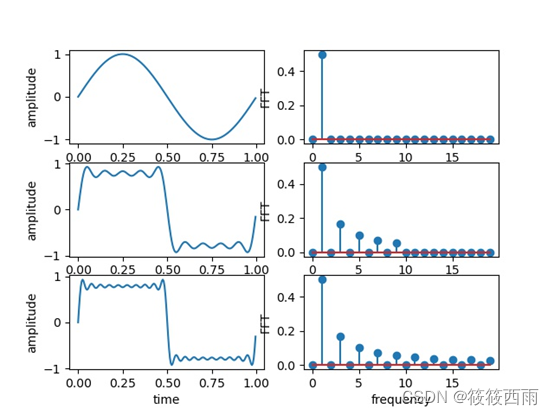
输出如下图所示的结果:
生成包含1个、5个和10个正弦波信号的时域图和它们的FFT(傅立叶变换)的频域图,将它们放置在3x2的子图布局中。比较不同数量的正弦波信号在时域和频域上的表示。
代码展示
import numpy as np
from matplotlib import pyplot as plt# 时间长度为1,采样间隔为0.005
x = np.arange(0, 1, 0.005)
# 采样点数
n = len(x)
# 由于对称性,只取单边频谱,又由于我们事先知道实验中信号的频率小于20,所以只取前20个
freq = np.arange(20)y = []
F = []
# 分别取1,5,10个正弦波叠加
for num in [1, 5, 10]:y_signal = 0for i in range(num):# 正弦波的频率为1,3,5,7...y_signal += np.sin(2*np.pi*(2*i+1)*x)/(2*i+1)y.append(y_signal)F_signal = np.fft.fft(y_signal)# 取abs是为了计算复数的幅度谱,/n是为了归一化F.append(np.abs(F_signal[range(20)])/n)_, axs = plt.subplots(3, 2)for i in range(3):axs[i, 0].plot(x, y[i])axs[i, 0].set_xlabel('time')axs[i, 0].set_ylabel('amplitude')axs[i, 1].stem(freq, F[i])axs[i, 1].set_xlabel('frequency')axs[i, 1].set_ylabel('FFT')plt.savefig('1D_FFT.jpg')
plt.show()结果展示
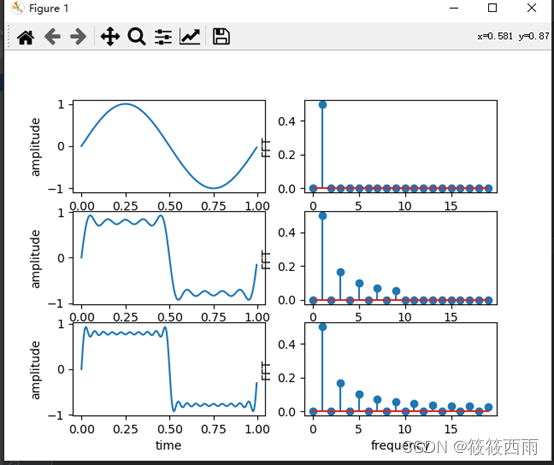
主要代码解释
创建时间向量 x:
x = np.arange(0, 1, 0.005):创建一个从0到1的时间向量 x,采样间隔为0.005秒,用于表示信号的时间范围。
获取采样点数 n:
n = len(x):计算时间向量 x 中的采样点数,以便在后续的FFT归一化中使用。
创建频率向量 freq:
freq = np.arange(20):创建一个频率向量 freq,包含从0到19的整数值,表示将计算的频率范围。
创建信号和频域数据:
使用for循环分别取1、5和10个正弦波信号,并在每个循环中生成信号,并计算其FFT。
y_signal = 0:初始化一个信号变量y_signal,用于存储叠加的正弦波信号。
在内部的for循环中,叠加不同频率的正弦波信号到y_signal。
F_signal = np.fft.fft(y_signal):计算y_signal的傅立叶变换,结果存储在F_signal中。
F.append(np.abs(F_signal[range(20)])/n):将计算的FFT结果归一化并存储在列表F中,仅保留前20个频率成分。