前言

完全背包问题，相比0/1背包问题，实就每个物品可以取无限次。

---

一、完全背包的状态设计

有n(n≤100)种物品和一个容量为m(m≤10000)的背包。第i种物品的容量是c[i]，价值是w[i]。现在需要选择一些物品放入包， 每种物品可以无限选择,组总容量不能超过背包容量，求能够达到的物品的最大总价值。

以上就是完全背包问题的完整描述，和0/1背包的区别就是每种物品可以无限选取;

1、状态设计

状态(i , j)表示前 i 种物品恰好放入容量为 j 的背包(0 ≤ i < n, 0 ≤ j ≤ m)；令 dp[i][j]示状态(i, j)下该背包得到的最大价值，即前 i 种物品(每种物品可以选择无限件)恰好放入容量为j的背包所得到的最大总价值;

2、状态转移方程

$$dp[i][j]=max(dp[i-1][j-c[i]\ast k]+w[i]\ast k)(0\le k\le j/c[i])$$

因为每种物品有无限种可放置，将它归类为以 下两种情况:

• 不放：如果“第 i 种物品不放入容量为 j 的背包"，那么问题转化成求**" 前i - 1种物品放入容量为 j 的背包"的问题，所以最大价值就等于"前i - 1种物品放入容量为 j 的背包"的最大价值**，对应状态转移方程中k = 0的情况，即dp[i-1][j]
• 放k个：如果第 i 种物品放入容为j的背包",那么问题转化成求"前 i - 1 种物品放入容量为j - c[i] * k的背包"的问题；那么此时最大价值就等于"前i - 1种物品放入容量为j-c[i] * k的背包"的最大价值加上放入 k 个第 i 种物品的价值，即dp[i-1][j - c[i] * k] + w[i] * k
  枚举所有满足条件的 k 就是我们所求的 “前i种物品恰好放入容为j的背包” 的最大价值了。
  注意：由于每件物品都可以无限选择，所以这里描述的时候都是用的"种"作为单位，即代表不同种类的物品。

3、对比0/1背包问题

完全背包问题是0/1包问题的扩展，区别就是它可以选择取0件、取1件、取2 件、取…k件，而0/1包问题只能取0件、取1件。如果从状态转移方程出发,我们可以把两个问题进行归纳统一，得到一个统一的状态转移方程如下:
$$dp[i][j]=max(dpli-1][j-c[i]\ast k]+w[i]\ast k)$$

• 对于0/1包问题，k的取值为0, 1
• 对于完全背包问题，k的取值为0, 1, 2, 3, ……, j / c[i];

4、时间复杂度分析

对于n种物品放入一个容量为m的背包，状态数为O(nm)，每次状态转移的消耗为O(k)，所以整个状态转移的过程时间复杂渡是大于O(nm)的，那么实际是多少呢?
考虑最坏情况下，即c[i]= 1时，那么要计算的dp[][j]的转移数为 nm ，**总的状态转移次数就是nm^{2**，所以整个算法的时间复杂度是O(nm}2)的，也就是说状态转移均摊时间复杂度是O(m)的。
接下来一节会对完全背包问题的时间和空间复杂度进行优化。

二、完全背包问题的优化

1、时间复杂度优化

我们把状态转移方程进行展开后得到如下的k+1个式子:
$$dp[i][j]=max\{\begin{array}{rlr}& dp[i-1][j]& (1)\\ & dp[i-1][j-c[i]]+w[i]& (2)\\ & dp[i-1][j-c[i]\ast 2]+w[i]\ast 2& (3)\\ & ...& \\ & dp[i-1][j-c[i]\ast k]+w[i]\ast k& (k+1)\end{array}$$
利用待定系数法，用j - c[i]代替上式的 j 得到如下式子:
$$dp[i][j-c[i]]=max\{\begin{array}{rlr}& dp[i-1][j-c[i]]& (1)\\ & dp[i-1][j-c[i]\ast 2]+w[i]& (2)\\ & dp[i-1][j-c[i]\ast 3]+w[i]\ast 2& (3)\\ & ...& \\ & dp[i-1][j-c[i]\ast k]+w[i]\ast (k-1)& (k)\end{array}$$
等式两边都加上w[]得到:
$$dp[i][j-c[i]]+w[i]=max\{\begin{array}{rlr}& dp[i-1][j-c[i]]+w[i]& (1)\\ & dp[i-1][j-c[i]\ast 2]+w[i]\ast 2& (2)\\ & dp[i-1][j-c[i]\ast 3]+w[i]\ast 3& (3)\\ & ...& \\ & dp[i-1][j-c[i]\ast k]+w[i]\ast k& (k)\end{array}$$
于是我们发现，这里的(1…k)式等价于最开始的状态转移方程中的(2) … (k+1)式，所以原状态转移方程可以简化为:
$$dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i])$$

这样就把原本均摊时间复杂度为O(m)的状态转移优化到了O(1)。
那么我们来理解一下这个状态转移方程的含义:
对于第i种物品，其实只有两种选择: 一个都不放、至少放一个。

• 一个都不放就是"前i - 1种物品放满一个容量为 j 的背包"的情况，即dp[i-1][i]

• 至少放一个的话，我们在”前i种物品装满j - c[i]容量的背包“的情况中再塞一个第i种物品，就能保证至少放一个第i种物品了，此时的价值为dp[i][j - c[i]] + w[i]，最大价值即二者取大。

如果只是为了掌握完全背包的模板，那么这个公式可以开头就讲，但是许多动态规划问题都不是裸题，需要我们从问题本身入手一步步的分析，优化从而解决问题，所以了解原理及公式推导是很有必要的。

2、空间复杂度优化

空间复杂度优化不用说就能猜到一定又是滚动数组优化，因为状态转移方程提示的已经很明显了，我们仍然从状态图上来观察，是否可以进行滚动数组优化。

根据优化后的状态转移方程，我们发现状态转移的过程如图所示:

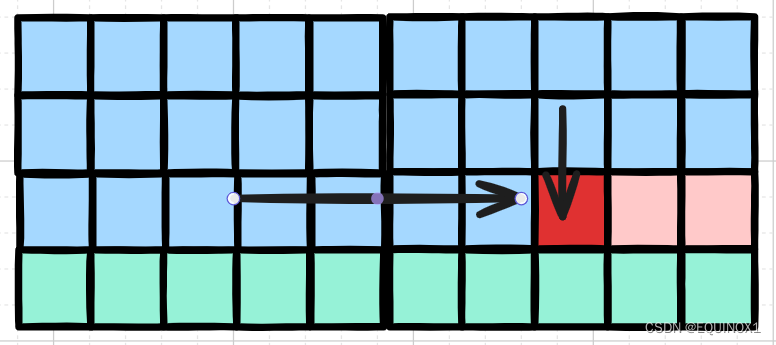
蓝色的格子代表的是已经计算出来的状态，红色的格子代表的是当前正在计算的状态，即dp[i][j]，它的值来自dp[i-1][j]和dp[i][j-c[i]]，这两个值对应的格子一定是蓝色的，绿色色的格子代表尚未进行计算的状态;

为了将问题描述的更加清晰，我们把(i, j)看成是二维笛卡尔坐标系上的点，i在x轴上, j在y轴上，如图所示:

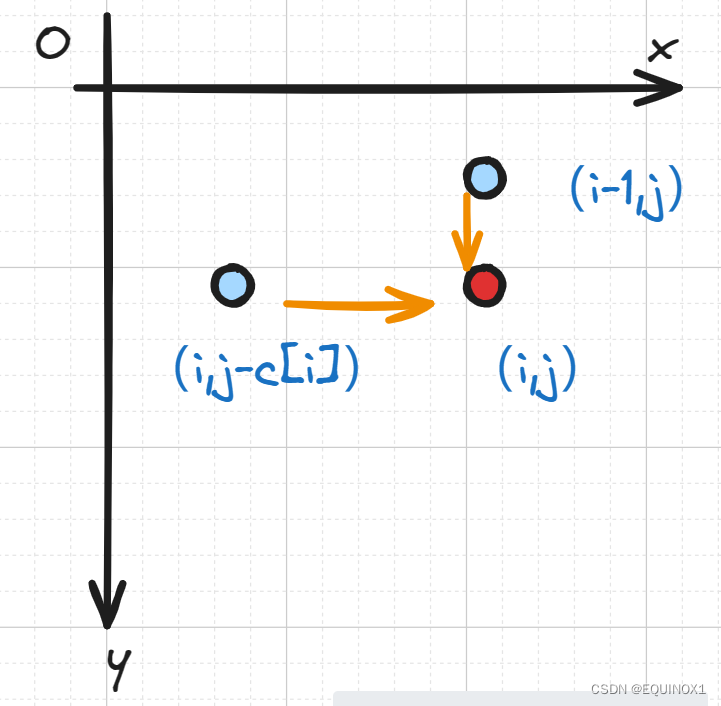
任何一个状态在计算出来以后，只会给x坐标比它大或者y坐标比它大的使用，所以我们只需要保留一行状态，按照x递增进行顺序计算,就可以做到把二维的问题转换成一维,将状态转移方程变成如下表示:
$$dp[j]=max(dp[j],dp[j-c[i]]+w[i])$$

三、OJ练习

裸题

P1616 疯狂的采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

友情提示：不开long long见祖宗

很直白的裸题，t就是背包容量，给了m种物品，求最大价值。

直接跑板子，最后一个点不开long long会错

AC代码如下：

#include <iostream>
#include <cstring>
using namespace std;
#define N 10010
#define M 10000010
#define int long long
int t, m;
int c[N], w[N], dp[M]{0};signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);// freopen("in.txt", "r", stdin);// freopen("out.txt", "w", stdout);cin >> t >> m;for (int i = 0; i < m; i++)cin >> c[i] >> w[i];for (int i = 0; i < m; i++)for (int j = c[i]; j <= t; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[t];return 0;
}

[P2722 USACO3.1] 总分 Score Inflation - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

同样裸题，直接跑板子即可。

AC代码如下：

#include <iostream>
#include <cstring>
using namespace std;
#define N 10010
#define M 10010
#define int long long
int t, m;
int c[N], w[N], dp[M]{0};signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);// freopen("in.txt", "r", stdin);// freopen("out.txt", "w", stdout);cin >> t >> m;for (int i = 0; i < m; i++)cin >> w[i] >> c[i];for (int i = 0; i < m; i++)for (int j = c[i]; j <= t; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[t];return 0;
}

---

完全背包+离散化

P1853 投资的最大效益 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

根据题目呢，如果我们不考虑n年后的情况，只考虑第一年能够得到的最大资产，那么很简单，就是一个完全背包问题的裸题，我们把债券当作物品，初始总资产当作容量，求出最大收益，然后最大收益加上初始总资产就是第一年能够得到的最大资产

那么n年的情况呢？

我们发现他这个债券机制太科幻了，我们每年得到收益后还能原价卖出债券，下一年再拿新的资产去选择新的债券购买方案，虽然不知道现实中有没有这种好事，但是对于我们做题而言反而简单了。

我们第一年结束得到了新的资产，第二年拿着第一年的资产再来一次完全背包，年底再卖掉，第三年拿着第二年的资产再来……

我们发现所谓的n年就是让你跑n次完全背包罢了

到这里可以直接写板子了，加一层循环罢了。但是！！！你的资产越来越大，也就是说你的状态数组dp的空间就有要求了，很可能再某一年你的背包直接爆炸了

我们发现题目里说了债券的价格为1000的倍数，那么我们就可以将数据离散化了

状态转移过程中把容量除以1000，物品体积也除以1000，价值不做改变，这样我们原先最大价值为dp[s]，这样一来就变成了dp[s/1000]了，就有了下面的代码

AC代码如下：

#include <iostream>
#include <cstring>
using namespace std;
#define N 10010
#define M 1000010
#define int long long
int s, n, d;
int c[N], w[N], dp[M]{0};signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);// freopen("in.txt", "r", stdin);// freopen("out.txt", "w", stdout);cin >> s >> n >> d;for (int i = 0; i < d; i++){cin >> c[i] >> w[i];}for (int k = 0; k < n; k++){memset(dp, 0, sizeof(dp));for (int i = 0; i < d; i++)for (int j = c[i] / 1000; j <= s / 1000; j++)dp[j] = max(dp[j], dp[j - c[i] / 1000] + w[i]);s += dp[s / 1000];}cout << s;return 0;
}

最小值

[P2918 USACO08NOV] Buying Hay S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

不难想到这是个完全背包的问题，那么对问题进行抽象，怎样选取物品和容量呢？这里给出两种角度，两种角度有着不同的处理细节。

F1 每个公司package的重量为价值，价格为体积

这样思考其实是很简单粗暴，也是最好理解的，我们即然要求购买干草量不小于目标值的所有方案中的最小花费，那么我们设定一个总花费的上限，然后以上限为总容量，以每个公司的包裹为n种物品，其重量为价值，价格为体积

这样我们跑一遍完全背包后，只要找到满足dp[j] >= s的最小j即可（s为需要购买的干草重量）

显然dp[j]是单调递增的，钱越多买的越多嘛，所以直接二分查找答案并输出即可。

#include <iostream>
#include <cstring>
using namespace std;
#define N 110
#define M 100000
#define int long long
int s, n, ans = M;
int c[N], w[N], dp[M + 1]{0};signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);freopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);cin >> n >> s;for (int i = 0; i < n; i++)cin >> w[i] >> c[i];for (int i = 0; i < n; i++)for (int j = c[i]; j <= M; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << (lower_bound(&dp[0], &dp[M], s) - &dp[0]);return 0;
}

F2 每个公司package的价格为价值，重量为体积

这样的话，先不考虑具体代码的实现，最终我们的答案就是dp[s]了吗？

不一定，很可能实际情况情况导致我们不能恰购买s的干草，即物品的体积导致容量s背包装不满，此时dp[s]为非法值，所以我们最终要找到一个dp[j]最小的j（j>=s）

这样的话我们由于求的是最小花费，所以这里状态转移的时候要转移最小值，所以不可避免地要对dp数组预处理为很大的非法值。

初态dp[0] = 0，背包容量的上限为s + 5000，这个根据数据范围很好得出

直接上代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 110
#define M 55010
#define int long long
int s, n, ans = M;
int c[N], w[N], dp[M]{0};signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);cin >> n >> s;for (int i = 0; i < n; i++)cin >> c[i] >> w[i];memset(dp, 0x3f, sizeof(dp));dp[0] = 0;for (int i = 0; i < n; i++)for (int j = c[i]; j <= s + 5000; j++)dp[j] = min(dp[j], dp[j - c[i]] + w[i]);cout << *min_element(&dp[s], &dp[s + 5001]);return 0;
}