双语!性能优越|融合黏菌和差分变异的量子哈里斯鹰算法SDMQHHO

在这里插入图片描述

前面的文章里卡卡介绍了哈里斯鹰优化算法(Harris Hawks Optimization, HHO).HHO是 Heidari等[1]于2019年提出的一种新型元启发式算法，设计灵感来源于哈里斯鹰在捕食猎物过程中的合作行为以及突然袭击的狩猎风格，具有需调参数少、原理简单易实现、局部搜索能力强等优点，在许多工程领域得到广泛的应用。

然而，HHO算法虽然在CEC2005中有较好的性能，但HHO在CEC2017等更复杂的基准函数问题中的能力还缺乏科学证据，这类基准函数不仅包含单模和多模，而且还包括混合和复合函数，对算法在摆脱局部最优的能力以及全局寻优能力都是极大的考验。而由作者前面文章中的分析可知，虽然HHO的开发能力强，但HHO存在全局/局部搜索不平衡，在迭代后期HHO将只进行开发，若面对复杂问题其在迭代后期易陷入局部最优，因此本文作者将对HHO进行改进，并在CEC2017、CEC2020和CEC2022中进行测试(Matlab/Python)，以验证其在复杂问题中优越性能。(PS：最近由于学业繁忙以及开发Python代码，更新比平时慢了点，以后对Python熟悉了后更新速度会快上来)

00 文章目录

1 哈里斯鹰优化算法原理

2 融合黏菌算法和差分进化的量子哈里斯鹰优化算法

3 代码目录

4 实验结果

5 源码获取

01 哈里斯鹰优化算法原理

关于哈里斯鹰算法原理及其优缺点分析作者在前面的文章中已经作了介绍

02 融合黏菌算法和差分进化的量子哈里斯鹰优化算法

本文基于哈里斯鹰优化算法的特点及其缺陷进行如下改进。

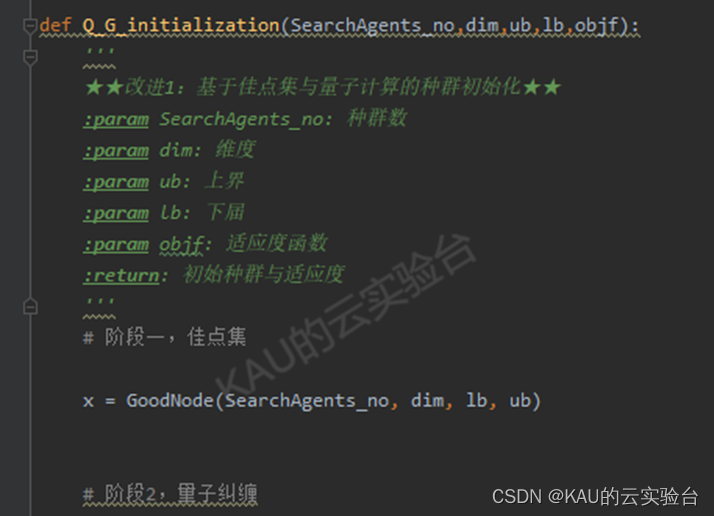
2.1 基于量子计算和佳点集的种群初始化

阶段1：佳点集

HHO通过随机生成初始种群的方法，容易出现种群分布不均匀，会导致种群多样性减少，种群质量不高，影响算法的收敛速度。

佳点集是一种有效的均匀选点方法。该理论由华罗庚先生提出[2]，在许多群智能优化算法中都得到了应用，由佳点集的定义，设GD是D维欧式空间中的单位立方体，若r∈GD，形为：
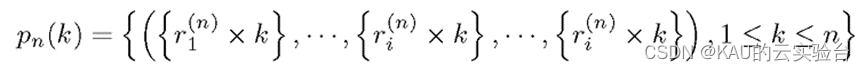
在这里插入图片描述

其偏差满足：

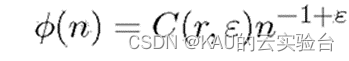
在这里插入图片描述

则称Pn(k)为佳点集，r为佳点，其中C(r, ε)是是只与r、ε(ε>0)有关的常数。取rk={2cos(2pir/p)}，1≤k≤n，p是满足(p-D/2)≥D的最小素数，理论[3]上已证明，用n个佳点构成的加权和比采用任何其他n个点所得到的误差都要小，并尤其适用于高维空间的近似计算。以二维单位搜索空间为例，随机取点与佳点集方法取点的对比如下：
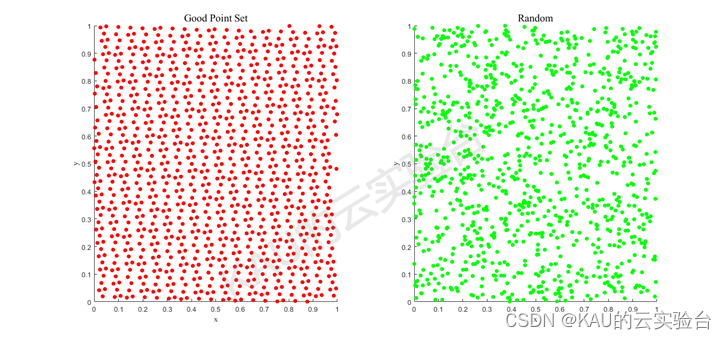
在这里插入图片描述

显然,随机取点并不均匀，并且许多取点位置重合，会造成解的可利用率不高，而佳点集方法能够使得取点更为均匀地分布在搜索空间中，其在全局中的搜索效率将更高。

阶段2：量子计算

量子计算(Quantum Computation，QC)是1982年首先由 Richard Feynman 提出[4]，是目前国内外学者比较关注的前沿学科之一，量子计算理论源于量子力学理论，而量子力学理论、混沌理论与相对论同被列为二十世纪最伟大的发现和科学佳作，可见量子计算的前沿性也是非常突出的。

经典计算与量子计算中的两种基本状态区别在于量子比特还可以表示成叠加态，即两个极化状态的线性组合。根据量子计算的这一特点，可以在初始化阶段引入量子计算的概念，基于一组量子比特，获得更多的初始种群。

…（理论略）

则根据两个阶段的初始化策略，在佳点集初始化得到的初始种群基础上，再进行量子计算的变换，以提高和改善初始种群在搜索空间上的分布质量，加强其全局搜索能力。

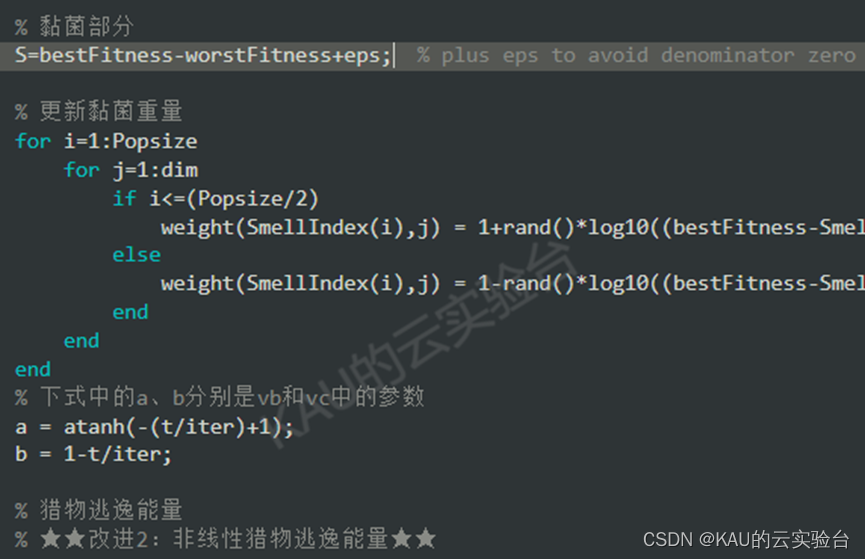
2.2 非线性猎物逃逸能量

由前面文章中作者的分析可以知道，控制哈里斯鹰算法探索与开发阶段的重要参数——猎物逃逸能量E在迭代后期(t>Tmax/2)恒小于1，这会导致算法后期仅进行开发，若前期没有探索到全局最优附近的点，则算法可能会陷入局部最优无法跳出，因此本文对开发与探索的转换策略进行改进。公式略

本文采取了一种基于随机数的转换策略，且猎物逃逸能量E在前期下降慢，使得算法能够进行广泛的区域探索，同时，迭代后期猎物逃逸能量E虽然较小，但算法仍有进行全局探索的可能，提高了算法跳出局部最优的能力。改进前后算法进行探索与开发策略的对比示意图如下：
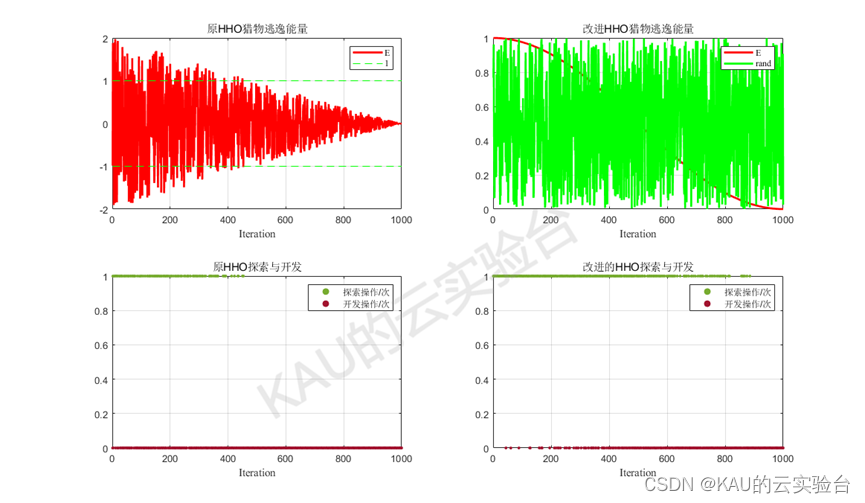
在这里插入图片描述

由图可以看到，改进前HHO在迭代前期探索和开发都有一定概率进行，而到了后期则只有开发操作，若面对复杂问题，前期可能并不能探索到全局最优点附近，因此会陷入局部最优。改进后在后期也有一定概率进行全局探索，因此增强了算法跳出局部最优的能力。

2.3 融合准反向学习与黏菌算法的探索阶段

黏菌算法(slime mould algorithm, SMA)[5]是一种具有优秀全局寻优性能的优化算法，SMA会根据适应度值调整不同的搜索模式，同时会分离出一部分有机物向其他领域探索，并且vb的振荡作用也增加了全局探索的可能性。因此，SMA的多重探索机制使该算法具有强大的全局寻优能力。

针对HHO优化算法面对复杂问题易陷入局部最优的问题，本文将黏菌算法的多重搜索机制引入其搜索阶段以增强HHO算法的全局搜索能力。同时考虑到传统SMA中，当rand<z时，黏菌种群由解空间随机生成黏菌个体，模拟黏菌分离部分个体探索其他可能存在的食物源的行为，此方法虽可以避免算法早熟，但并没有充分利用当前解的信息。准反向学习（Quasi-oppositional learning，QOL）[6]是在传统反向学习改进的基础上，用于提升个体当前质量的一种方法。由于原反向学习变换跨度过大，搜索精度不高，且生成的解容易停滞在邻域最优解。为了获得质量有明显提高的解，准反向学习被提出，并在后来被证明其更接近最优解[7]。公式略。

准反向解的图示如下：

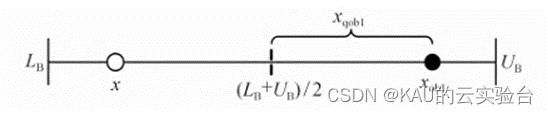
在这里插入图片描述

由图可以看出，准反向解能够实现更广泛和更合理的探索范围，具有更大几率接近搜索空间中的最优点或次优点，因此本文将准反向学习替换黏菌算法中r<z时的随机个体策略，该策略不仅有助于避免早熟，更有机会接近食物源。

结合哈里斯鹰算法中探索阶段的更新策略，本文改进的哈里斯鹰算法探索阶段的搜索策略为，公式略

将探索阶段进行以上改进，将提升算法在全局寻优上的搜索性能，提高搜索精度。

2.4 平均差分变异策略

由于种群中的哈里斯鹰在迭代过程中向最优个体聚集，若存在一个局部最优，随着迭代次数的增加，哈里斯鹰聚集在局部最优周围，易导致种群多样性下降。为避免算法陷入局部最优，防止早熟现象，本文引入平均差分变异[8]对种群个体和全局最优进行修正，其根据迭代的不同阶段采取了两种不同策略，具体如下：公式略

该变异策略在前期在个体附近进行搜索，而在后期倾向于在全局最优附近勘探，有助于算法跳出局部最优。

2.5 算法总流程
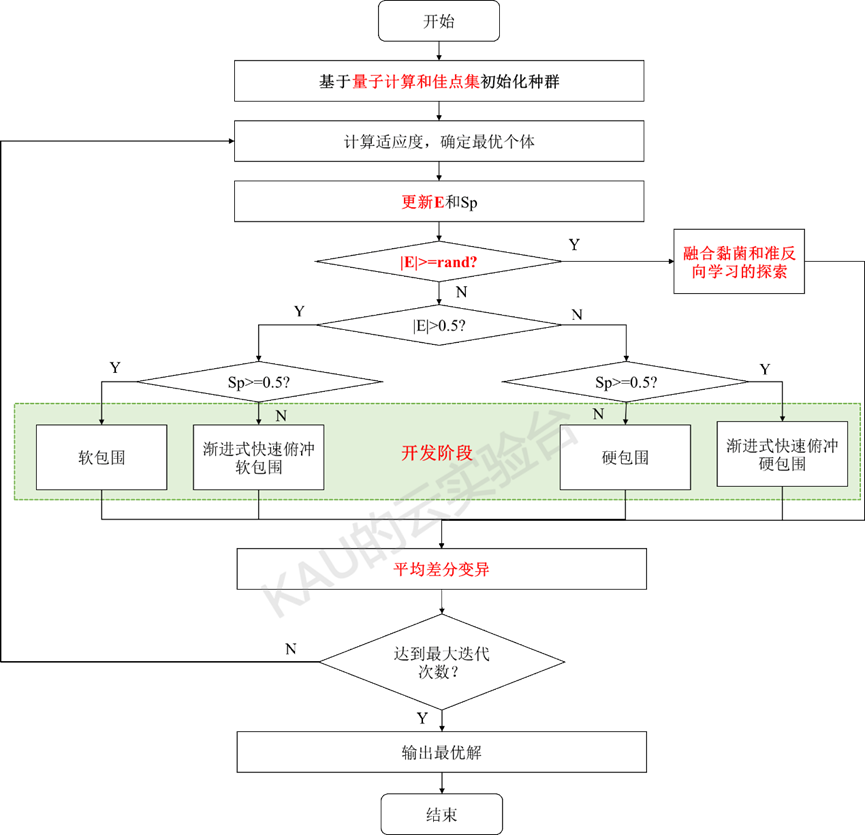
在这里插入图片描述

其中，红色部分为本文改进部分。

03 代码目录

在这里插入图片描述

代码包含了Matlab和Python，由于作者是首次将原创改进用Python写，所以这次开发周期长了些，并且只找到了CEC2017函数的调用，因此Python代码会比Matlab便宜些~，也期待大家使用的反馈。

MATLAB和Python的代码目录如下，作者在使用了Python后的最大感受就是Python的函数管理可以做的很方便，从两方的代码文件数的对比就可以看出。

MATLAB:Main_SDMQHHO_perf.m和Main_Only_SDMQHHO.m为主程序，关于这两个主程序的使用在Readme.txt中作者做了解释：

在这里插入图片描述

代码注释详细，一键运行Main_ SDMQHHO _perf.m即可得到所有运行结果，运行结果包括佳点集比较图、收敛因子比较图、算法在CEC2017/2020/2022测试函数上的迭代图，最后将生成excel表，包含算法在各函数迭代n次的平均值，均值、运行时间、最优解。

同时，文件也有乱码解决，给出了主要代码的txt文件。部分程序如下(perf_SDM_QHHO.m)

在这里插入图片描述

Python:Main_SDMQHHO_perf.py和Main_Only_SDMQHHO.py为主程序，关于这两个主程序的使用在Readme.txt中作者做了解释：
在这里插入图片描述

代码注释详细，一键运行Main_ SDMQHHO _perf.py即可得到所有运行结果，运行结果包括佳点集比较图、收敛因子比较图、算法在CEC2017测试函数上的迭代图，最后将生成excel表，包含算法在各函数迭代n次的平均值，均值、运行时间、最优解。部分程序如下(perf_SDM_QHHO.py)
在这里插入图片描述

04 实验结果

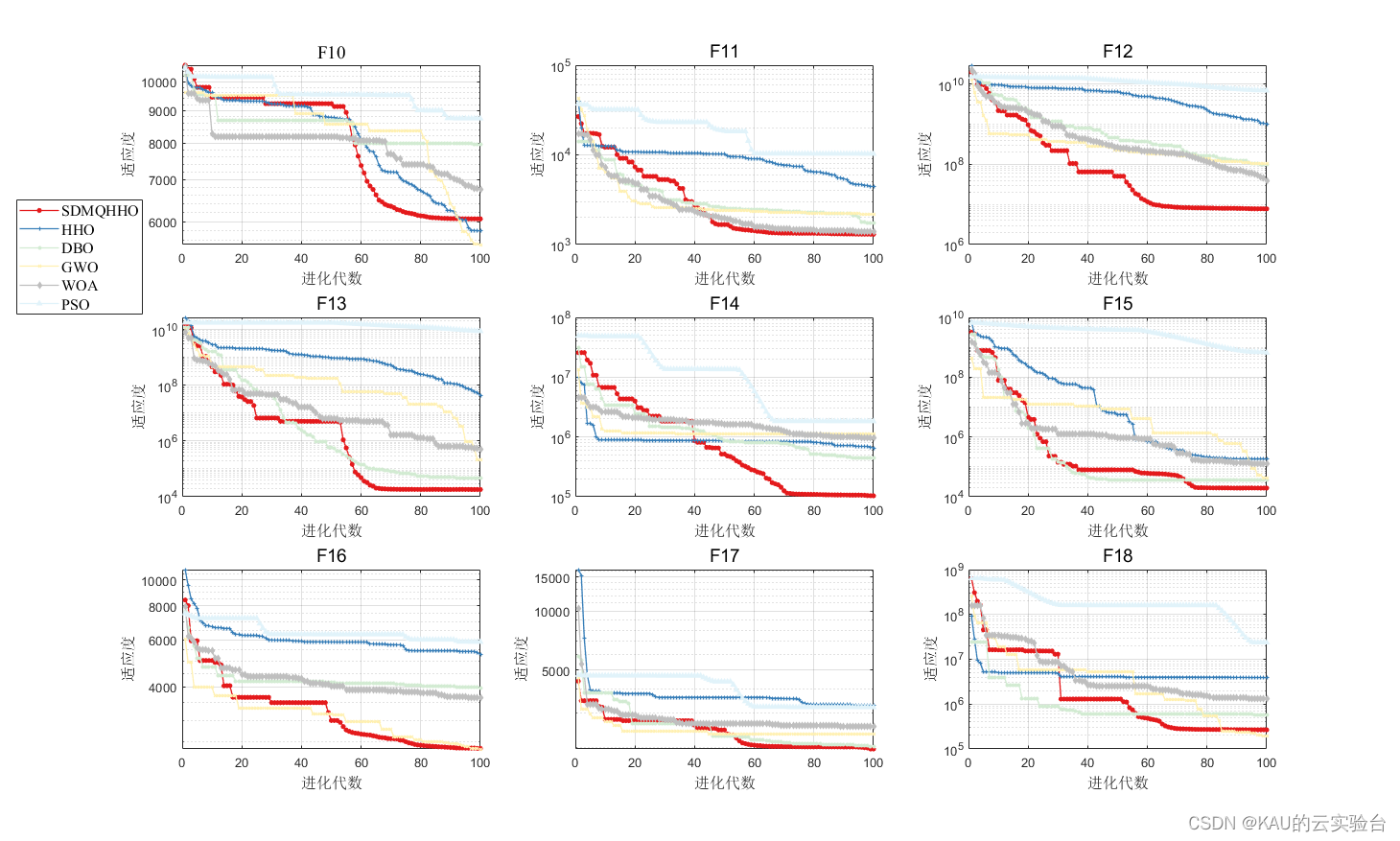
在本节中，MATLAB使用 CEC2017/2020/2022测试SDMQHHO性能，而Python使用CEC2017测试性能（因为作者只找到了CEC2017的测试函数）。结果如下：

MATLAB(由于结果太多了，作者这里对各测试函数都贴出一部分)

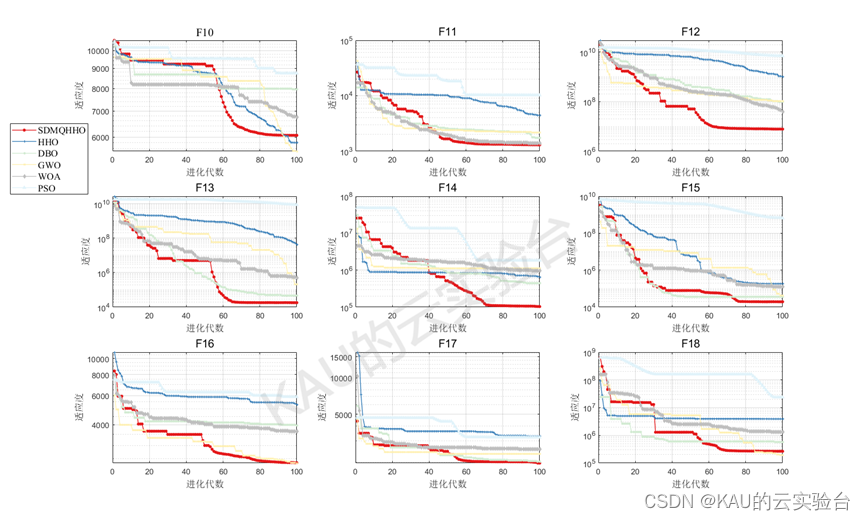
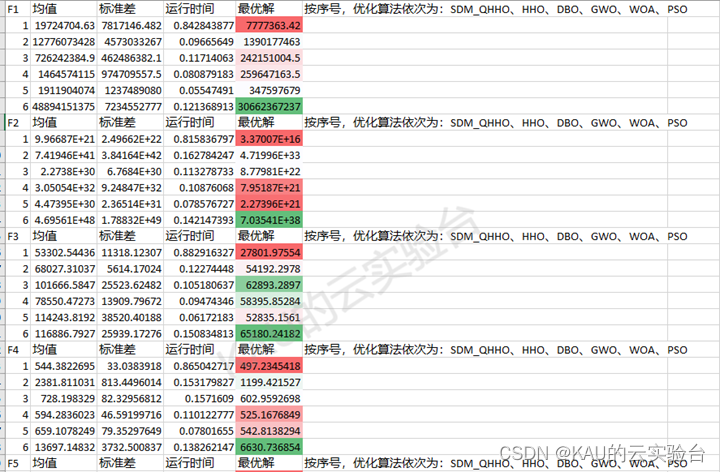
CEC2017
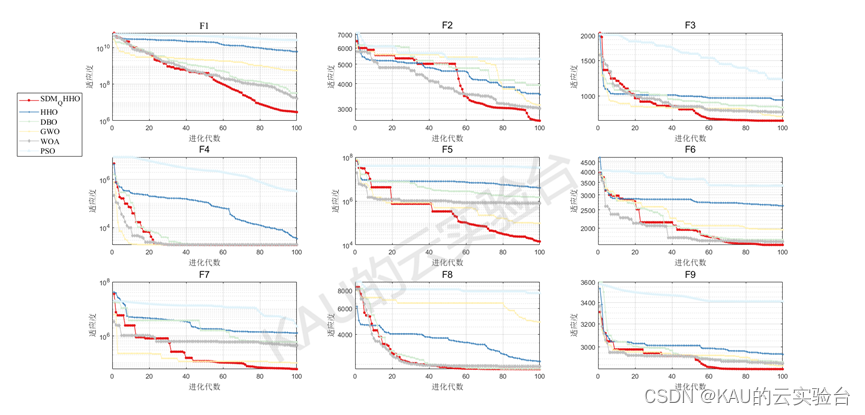
在这里插入图片描述

CEC2020
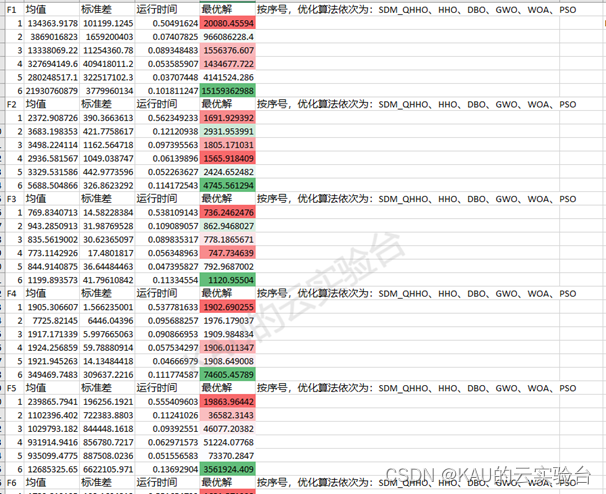
在这里插入图片描述

在这里插入图片描述

CEC2022
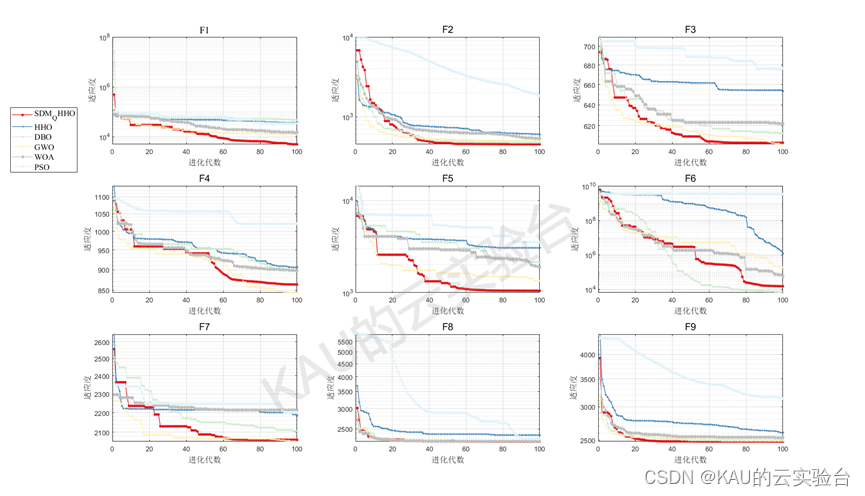
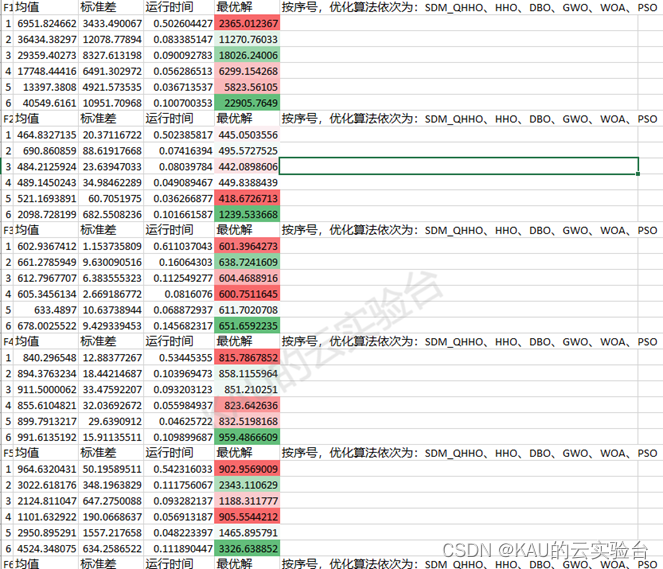
在这里插入图片描述

从结果看出，改进后的算法精度与收敛速度都得到了很大提升，同时可以发现HHO在一些函数表现欠佳，也反映出其面对复杂问题存在一定的早熟的问题。

Python(因为Python不能像matlab可以gui调整legend，也可能是我不会…因此3x3的子图中图例会把图盖住，作者这里用的1x2，也展示部分图)

Python部分（仅有 CEC2017）

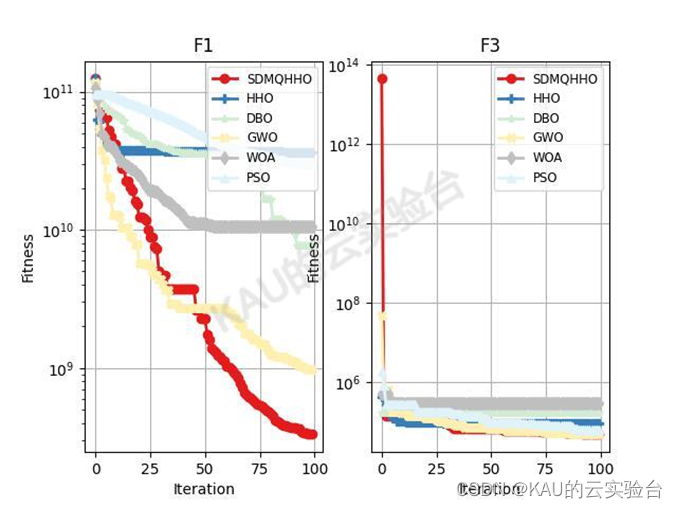
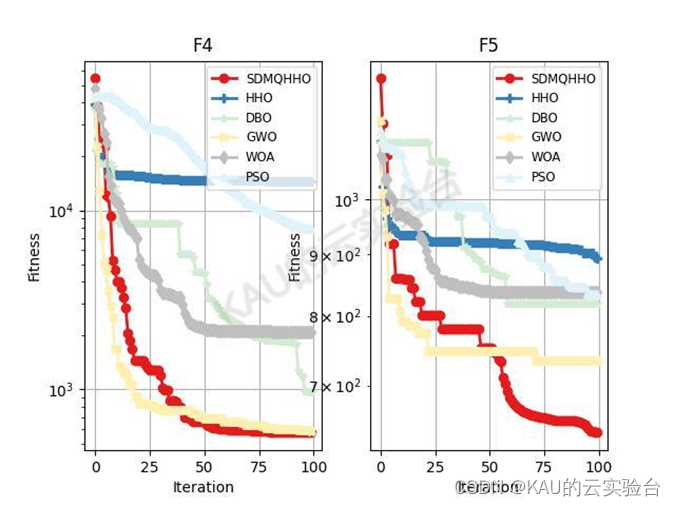
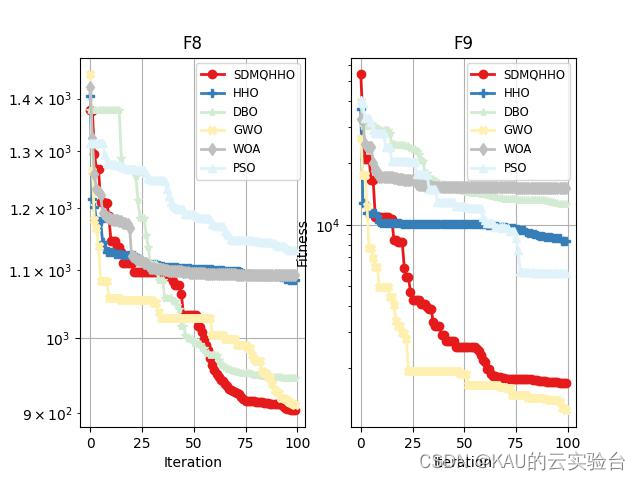
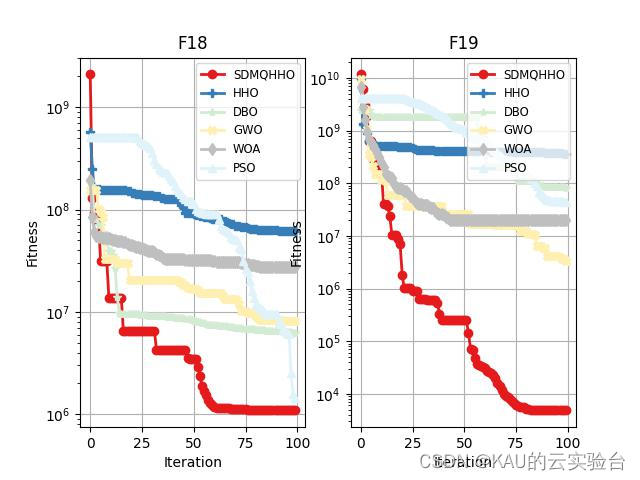
在这里插入图片描述

python代码的运行速度比matlab慢很多，可能是我在python里用了很多矩阵运算

05 源码获取

GZH（KAU的云实验台）后台回复 SDMQHHO (Matlab与Python版本)

含完整改进算法的理论与公式信息的pdf

参考文献

[1] Heidari A A, Mirjalili S, Faris H, et al. Harris Hawks Optimization Algorithm and Applications[J]. Future Generation Computer Systems,2019,97(8):849-872.

[2] 华罗庚,王元.数论在近似分析中的应用[M].北京:科学出版社. 1978: 83-86.Hua LG,Wang Y.Application of number theory in approximate analysis[M. Beijing: Science Press，1978:83-86.

[3] Kiefer J. On large deviations of the empiric D. F. of vector chance variables and a law of the iterated logarithm[J].Pacific Journal of Mathematics,1961,11(2):649-660.

[4] Feynman,R. P.(1982).Simulating physics with computers. International Journal of Theoretical Physic,21(6),22.https: //doi.org/10.1007/bf02650179

[5] LI Shimin, CHEN Huiling, WANG Mingjing, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future generation computer systems, 2020, 111:300–323.

[6] BASE M．Quasi-oppositional differential evolution for optimal reactive power dispatch［J］．International Journal of Electrical Power and Energy Systems，2015，78: 29-40．

[7] T. Si, P.B.C. Miranda, D. Bhattacharya, Novel enhanced Salp Swarm Algorithms using opposition-based learning schemes for global optimization problems, Expert Syst. Appl. 207 (2022), 117961.

[8] Abdesslem Layeb. Differential Evolution Algorithms with Novel Mutations, Adaptive Parameters and Weibull Flight Operator, 08 September 2022, PREPRINT (Version 1) available at Research Square [https://doi.org/10.21203/rs.3.rs-1898342/v1]

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看 (ง•̀_•́)ง(不点也行)