目录

题目地址：

题目：

解题方法：

解题分析：

解题思路：

代码实现：

注：

代码实现（递归）：

代码实现（迭代）：

---

题目地址：

94. 二叉树的中序遍历 - 力扣（LeetCode）

难度：简单

今天刷二叉树的中序遍历，大家有兴趣可以点上看看题目要求，试着做一下。

题目：

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

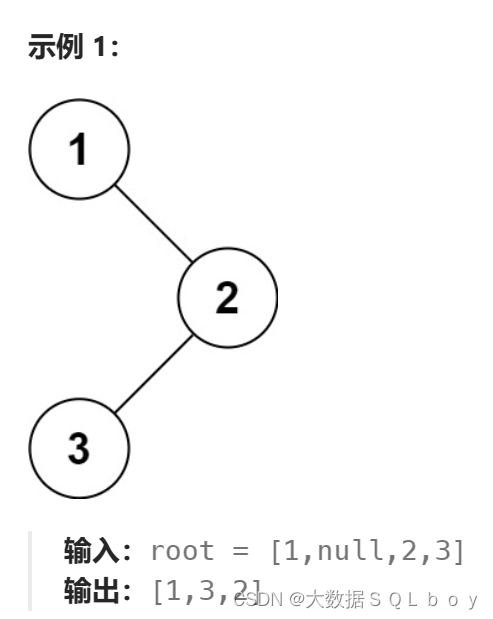
我们直接看题解吧：

解题方法：

方法1，递归

方法2，迭代

方法3，Morris（空间复杂度（1））

解题分析：

中序遍历顺序：左子树->根节点->右子树（即左根右）

递归方法通俗易懂，但效率低，迭代方法，效率虽高，但不易理解，

因此这里着重讲一下Morris方法。

解题思路：

设当前遍历节点为x:

1、若x无左孩子，将x的值放入答案数组，接着访问x右孩子，即x=x.right。

2、若x有左孩子，则找到该左子树中最右的节点(即左子树中序遍历的最后一个节点)记为predecessor。

    · 若predecessor的右孩子为空，则将右孩子指向x,接着访问x左孩子即x=x.left

     ·若predecessor的右孩子不为空，则将右孩子指向x，此时说明已遍历完x的左子树，则将predecessor的右孩子置空，将x的值加入答案数组，然后访问x的右孩子即x=x.right

3、重复上述操作，直至访问完整棵树。

 具体可结合题解-->  ：94. 二叉树的中序遍历 题解

代码实现：

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>(); //创建集合存储节点的值TreeNode predecessor = null;   //创建predxessor节点,并置空while (root != null) {if (root.left != null) {//左孩子不为空// predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止predecessor = root.left;while (predecessor.right != null && predecessor.right != root) {predecessor = predecessor.right;}// 让 predecessor 的右指针指向 root，继续遍历左子树if (predecessor.right == null) {predecessor.right = root;root = root.left;}// 说明左子树已经访问完了，我们需要断开链接else {res.add(root.val);predecessor.right = null;root = root.right;}}// 如果没有左孩子，则直接访问右孩子else {res.add(root.val);root = root.right;}}return res;}
}

注：

其实整个过程我们就多做一步：假设当前遍历到的节点为 x，将 x 的左子树中最右边的节点的右孩子指向 x，这样在左子树遍历完成后我们通过这个指向走回了 x，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

代码实现（递归）：

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();inorder(root, res);return res;}public void inorder(TreeNode root, List<Integer> res) {if (root == null) {return;}inorder(root.left, res);res.add(root.val);inorder(root.right, res);}
}

代码实现（迭代）：

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();Deque<TreeNode> stk = new LinkedList<TreeNode>();while (root != null || !stk.isEmpty()) {while (root != null) {stk.push(root);root = root.left;}root = stk.pop();res.add(root.val);root = root.right;}return res;}
}