欧拉角概述
机器人末端执行器姿态描述方法主要有四种:旋转矩阵法、欧拉角法、等效轴角法和四元数法。所以,欧拉角是描述机械臂末端姿态的重要方法之一。
关于欧拉角的历史,由来已久,莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于任何参考系,一个刚体的取向,是依照顺序,从这参考系,做三个欧拉角的旋转而设定的。所以,刚体的取向可以用三个基本旋转矩阵来决定。换句话说,任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。
欧拉角描述机械臂姿态
在笛卡尔坐标系下,可以通过连续三次且相邻两次旋转不可以绕相同的坐标轴的旋转运动,来描述转动刚体相对于参考坐标系的方向。这三个角度就是欧拉角,当给定定坐标系和动坐标系后,可以产生24种不同旋转次序来描述刚体相对于定坐标系的姿态。
欧拉角法是描述物体姿态最简单的方式,只需要三个元素就可描述出末端坐标系的姿态。定义三个正交的旋转轴,按照绕着指定顺序的旋转轴旋转使刚体从初始姿态到目标姿态。其中绕轴旋转的角度称为欧拉角,以下所指的欧拉角是按照zyz轴的旋转顺序,姿态矩阵的表达式为
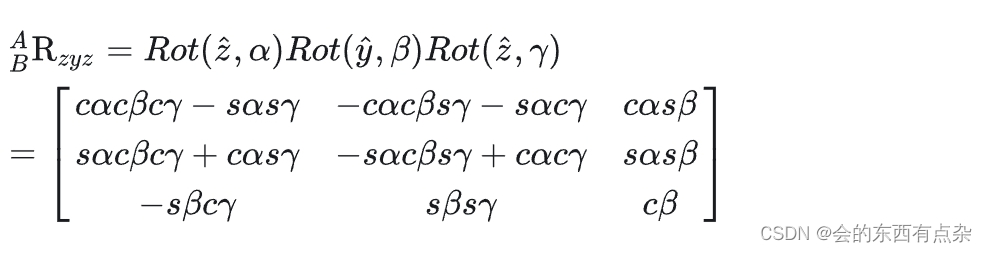
其中,RotX、RotY、RotZ,可以分别用如下代码表示:
public static Matrix<double> RotX(double angle){var c = Math.Cos(angle);var s = Math.Sin(angle);var ans = CreateMatrix.DenseOfArray(new double[,]{{1, 0, 0},{0, c, -s},{0, s, c},});return ans;}public static Matrix<double> RotY(double angle){var c = Math.Cos(angle);var s = Math.Sin(angle);var ans = CreateMatrix.DenseOfArray(new double[,]{{+c, 0, s},{+0, 1, 0},{-s, 0, c},});return ans;}public static Matrix<double> RotZ(double angle){var c = Math.Cos(angle);var s = Math.Sin(angle);var ans = CreateMatrix.DenseOfArray(new double[,]{{c, -s, 0},{s, +c, 0},{0, +0, 1},});return ans;}ABB机器人的欧拉角序列
ABB机械臂欧拉角序列采用ZYX序列,ZYX代表旋转轴的顺序,Z轴为第一个旋转轴、Y轴为第二个旋转轴、X轴为第三个旋转轴。

旋转矩阵示例代码如下:
public static Matrix<double> MakeRotationMatrixFromZyxEuler(double r, double p, double y){var matR = RotZ(r);var matP = RotY(p);var matY = RotX(y);var ans = matR.Multiply(matP).Multiply(matY);return ans;}川崎机器人的欧拉角序列
川崎机械臂欧拉角序列采用ZYZ序列,ZYZ代表旋转轴的顺序,Z轴为第一个旋转轴、Y轴为第二个旋转轴、Z轴为第三个旋转轴。其旋转角度用O、A、T表示。
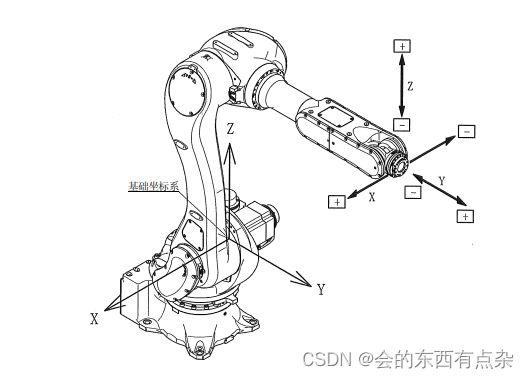
旋转矩阵示例代码如下:
public static Matrix<double> MakeRotationMatrixFromZyzEuler(double o, double a, double t){var matO = RotZ(o);var matA = RotY(a);var matT = RotZ(t);var ans = matO.Multiply(matA).Multiply(matT);return ans;}示例程序
计算机械臂的欧拉角(zyz和zyx两类序列)和旋转矩阵
https://download.csdn.net/download/qq_20660115/88686069