介绍:
K最近邻(K-Nearest Neighbors,KNN)是一种基本的分类和回归算法。它的基本思想是对未知样本进行预测时,先找到训练数据集中与该样本最近的K个样本,然后根据这K个样本的标签进行预测。
KNN模型的基本步骤如下:
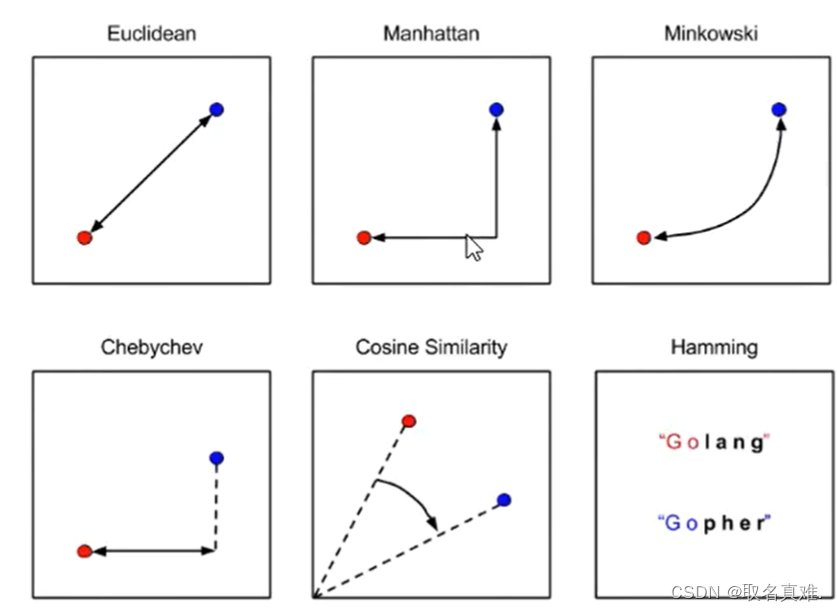
1. 计算未知样本与训练数据集中所有样本的距离,常用的距离度量方法有欧氏距离、曼哈顿距离等。
2. 根据计算得到的距离按照从小到大的顺序排序,选取距离最近的K个样本。
3. 根据K个样本的标签进行投票或者计算加权平均值,得到未知样本的预测结果。KNN模型的优点包括:
1. 简单直观,易于理解和实现。
2. 对异常值不敏感,因为它是基于距离进行判断的。
3. 可以适用于多种数据类型,如数值型、离散型等。KNN模型的缺点包括:
1. 计算量较大,特别是当训练数据集较大时。
2. 对于高维数据,可能会出现维度灾难问题,导致准确率下降。
3. 对于不平衡数据集和噪声数据集可能会有影响。KNN模型在实际应用中广泛使用,特别是在文本分类、图像识别、推荐系统等领域取得了良好的效果。

一、建模
import numpy as np #k Nearest Neighbour(KNN)建模
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inlinedata=pd.read_csv('iris.csv')
X=data.drop(['Species'],axis=1)
y= data['Species']from sklearn.model_selection import StratifiedShuffleSplit,cross_val_score
from sklearn.neighbors import KNeighborsClassifierknn = KNeighborsClassifier(metric='minkowski',p=2)#用minkowski公式,p=2则为欧几里得公式cv = StratifiedShuffleSplit(n_splits=10,test_size=.25,random_state=2)#分测试集accuracies = cross_val_score(knn,X,y,cv=cv,scoring='accuracy')print('cross_validation accuracy scores:{}'.format(accuracies))#准确率
print('mean cross-validation accuracy score:{}'.format(round(accuracies.mean(),3)))#准确率均值'''结果:
cross_validation accuracy scores:[1. 1. 1. 1. 1. 1.0.97368421 1. 1. 1. ]
mean cross-validation accuracy score:0.997
'''二、调参
2.1手动调参
#枚举,调参k
k_range = range(1,31)
k_score = []
for k in k_range:knn=KNeighborsClassifier(n_neighbors=k)scores=cross_val_score(knn,X,y,cv=cv,scoring='accuracy')k_score.append(scores.mean())
print("Accuracy scores are:{}\n".format(k_score))
print("Mean accuracy score:{}\n".format(np.mean(k_score)))'''结果:
Accuracy scores are:[1.0, 1.0, 0.9973684210526315, 1.0, 0.9973684210526315, 0.9973684210526315, 0.9973684210526315, 0.9894736842105264, 0.9921052631578947, 0.9868421052631579, 0.9894736842105264, 0.9842105263157894, 0.9868421052631579, 0.9789473684210526, 0.9868421052631579, 0.9815789473684211, 0.9868421052631579, 0.9815789473684211, 0.9842105263157894, 0.9815789473684211, 0.9815789473684211, 0.9842105263157894, 0.9815789473684211, 0.9815789473684211, 0.9894736842105264, 0.9789473684210528, 0.9868421052631579, 0.9842105263157895, 0.9842105263157894, 0.9842105263157895]Mean accuracy score:0.9878947368421052
'''plt.plot(k_range,k_score,'bo',linestyle='dashed',linewidth=1,markersize=6)#奇数点准确率更高2.2 GridSearchCV调参
GridSearchCV是一个用于模型参数调优的函数,可以根据给定的参数候选空间中的所有可能组合,使用交叉验证方法来评估模型的性能,最终选择出最佳的参数组合。它的调用方式类似于传统的fit函数,但是在fit函数的基础上添加了参数搜索和交叉验证的功能。使用GridSearchCV可以避免手动调整参数的繁琐过程,提高模型的性能和泛化能力。
#Grid search on KNN classifier
from sklearn.model_selection import GridSearchCV
k_range=range(4,31)
weights_options=['uniform','distance']param={'n_neighbors':k_range, 'weights':weights_options}cv = StratifiedShuffleSplit(n_splits=10,test_size=.30,random_state=15)#分测试集grid=GridSearchCV(KNeighborsClassifier(),param,cv=cv,verbose=False,n_jobs=-1)grid.fit(X,y)print(grid.best_score_)
print(grid.best_params_)
print(grid.best_estimator_)
'''结果:
1.0
{'n_neighbors': 11, 'weights': 'distance'}
KNeighborsClassifier(n_neighbors=11, weights='distance')
'''knn_grid=grid.best_estimator_
knn_grid.score(X,y)
#结果:1.0 2.3RandomizedSearchCV调参
RandomizedSearchCV是一个用于超参数优化的函数。它是scikit-learn库中GridSearchCV的一种替代方法。在机器学习模型中,超参数是在训练模型之前设置的参数,而不是通过训练数据学习得到的。超参数优化的目标是找到最佳的超参数组合,以获得最好的模型性能。
RandomizedSearchCV通过在超参数的可能值范围内进行随机搜索,来寻找最佳的超参数组合。与GridSearchCV不同,RandomizedSearchCV不是遍历搜索所有可能的超参数组合,而是在指定的超参数分布中进行随机抽样。使用
RandomizedSearchCV函数,可以指定要优化的模型、超参数的可能值范围、搜索的抽样次数等。函数将根据指定的超参数分布和评估指标,返回最佳超参数组合的模型。
#using randomizedSearchCV
from sklearn.model_selection import RandomizedSearchCV
k_range=range(4,31)
weights_options=['uniform','distance']param={'n_neighbors':k_range, 'weights':weights_options}cv = StratifiedShuffleSplit(n_splits=10,test_size=.30,random_state=15)#分测试集grid==RandomizedSearchCV(KNeighborsClassifier(),param,cv=cv,verbose=False,n_jobs=-1,n_iter=40)grid.fit(X,y)print(grid.best_score_)
print(grid.best_params_)
print(grid.best_estimator_)
'''结果:
1.0
{'n_neighbors': 11, 'weights': 'distance'}
KNeighborsClassifier(n_neighbors=11, weights='distance')
'''knn_grid=grid.best_estimator_
knn_grid.score(X,y)
#结果:1.0