汉诺塔问题(递归超详细)C++，leetcode

文章目录

前言
一、题目分析
二、算法原理
- 1.为什么要用递归
- 2.如何编写代码
三、代码实现
总结

前言

在本文章中，我们将要详细介绍一下汉诺塔问题，本题目我们采用递归的方式解决相关的内容

一、题目分析

在这里插入图片描述
题目要求详解：
🌟 有三个柱子假设名称分别为a,b,c，其中a柱子上有若干个盘子。
🌟这些盘子按照从底往上大小依次减小的次序摆放。
🌟不论盘子在哪个柱子上都必须要求下面盘子的大小都大于上面盘子的大小
🌟将a柱子上的若干盘子通过b柱子按照要求转移到柱子上

二、算法原理

☀️ ☀️ 学过的小伙伴都知道这道题目可以用递归解决，那我们为什么要用递归算法解决，为什么不用贪心，动态规划等算法呢？？

1.为什么要用递归

首先简单看一下递归：函数自己调用自己，将主问题分解为相同子问题，子问题又可以调用相同的子问题。

我们要有规律的放挪动盘子，每一步的意义是什么，同时注意不要分解的太过于细致

把每一步分析一下
🔱🔱n==1,直接可以把a柱子上的盘子放到c柱子上，不用借助b柱子就可以实现
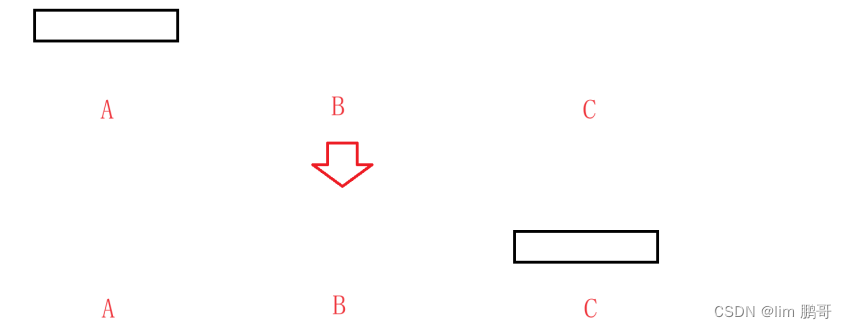
在这里插入图片描述

🔱🔱n==2，题目要求我们把a柱子上的2个盘子通过b柱子转移到c柱子上。

💗💗首先我们要把a柱子上的盘子挪到c柱子上，先想办法把a柱子上最下面那个最大的盘子挪到c柱子上，剩余的那一个才可以挪过去。
💗💗要挪动a柱子上最大的盘子，得先把a柱子上那个小盘子挪走，那这个怎末挪动呢？？
💗💗我们发现这一步和n== 1时的情景非常类似。按照n==1的步骤，把那个小盘子直接挪到b柱子上。
💗💗这时我们就可以把a柱子上最大的那个盘子挪到c柱子上了。
💗💗最后把那个小盘子挪动c柱子上就可以了
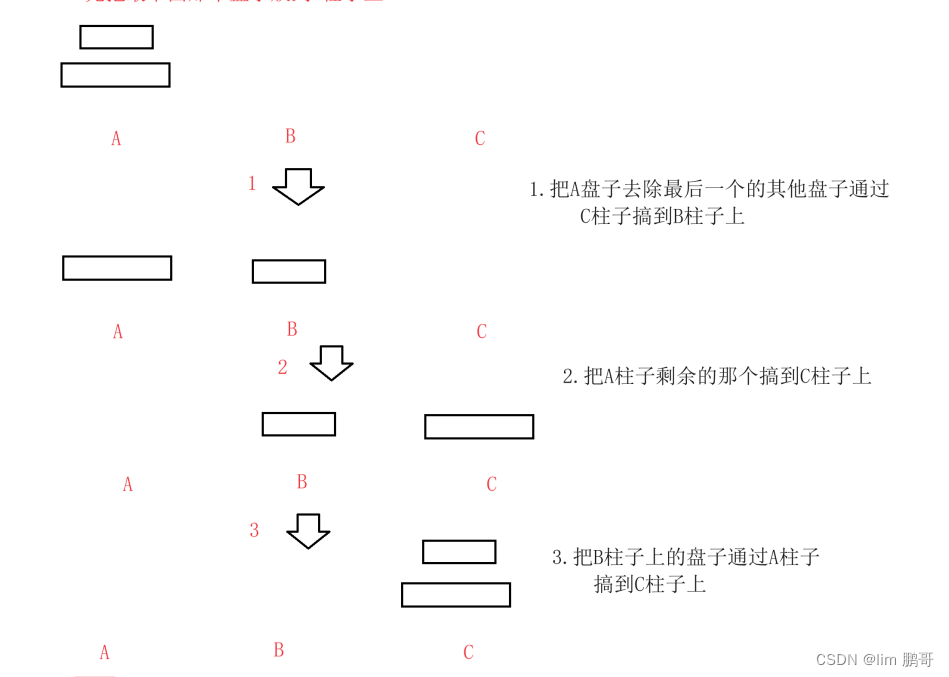
在这里插入图片描述

🔱🔱n==3，题目要求我们把a柱子上的3个盘子通过b柱子转移到c柱子上。

💗💗首先我们要把a柱子上的盘子挪到c柱子上，先想办法把a柱子上最下面那个最大的盘子挪到c柱子上，剩余的那俩个才可以挪过去。
💗💗要挪动a柱子上最大的盘子，得先把a柱子上那两个盘子挪走，那这个怎末挪动呢？？
💗💗我们发现这一步和n== 2时的情景非常类似。按照n==2的步骤，把那俩个小盘子通过c柱子挪动到b柱子上（不能挪动到c柱子上，我们需要用这个柱子放最大盘子）。
💗💗这时我们就可以把a柱子上最大的那个盘子挪到c柱子上了。
💗💗最后把那个俩盘子通过a柱子挪动c柱子上就可以了
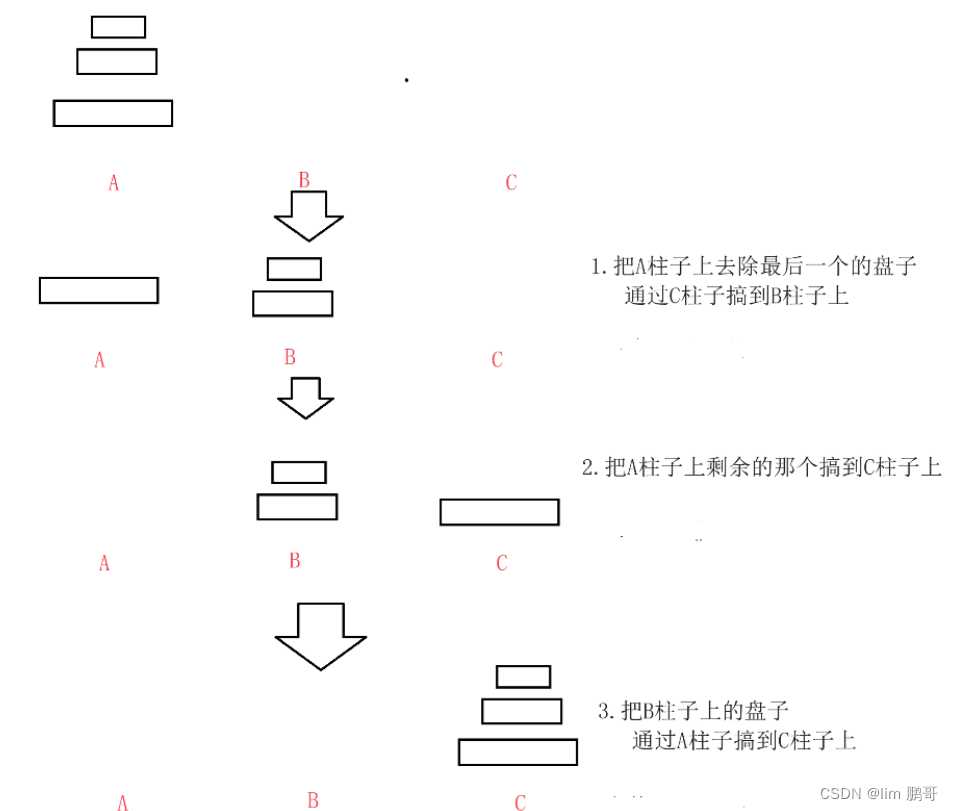
在这里插入图片描述

🔱🔱n==N，题目要求我们把a柱子上的N个盘子通过b柱子转移到c柱子上。

💗💗首先我们要把a柱子上的盘子挪到c柱子上，先想办法把a柱子上最下面那个最大的盘子挪到c柱子上，剩余的那N-1个才可以挪过去。
💗💗要挪动a柱子上最大的盘子，得先把a柱子上那N-1个盘子挪走，那这个怎末挪动呢？？
💗💗我们发现这一步和n== N-1时的情景非常类似。按照n==N-1的步骤，把那N-1个小盘子通过c柱子挪动到b柱子上（不能挪动到c柱子上，我们需要用这个柱子放最大盘子）。
💗💗这时我们就可以把a柱子上最大的那个盘子挪到c柱子上了。
💗💗最后把那N-1盘子通过a柱子挪动c柱子上就可以了

通过这里我们发现，他们采用的相同的方式实现，这与递归的定义是一致的。

递归是一种在函数定义中使用函数自身的方法。在递归过程中，函数将问题分解为更小的子问题，并通过调用自身来解决这些子问题。递归通常用于解决可以被分解为相同类型的子问题的问题，直到达到基本情况为止。

2.如何编写代码

💫 💫.重复子问题----->函数头

将a柱子上的N个盘子借助b柱子转移c柱子上(知道递归需要哪些参数)
dfs(a,b,c,n);

💫 💫.只关心某个问题----->函数体

把递归函数当成一个黑盒，相信他一定能完成任务

1.先把a柱子上除去最后一个盘子通过c柱子挪到b柱子上–>dfs(a,c,b,n-1);
2.把a柱子剩余的挪动到c柱子上------> c.push_back(a.back()); a.pop_back();
3.把b柱子上的盘子通过a柱子转移到c柱子上–》dfs(b,a,c,n-1);

💫 💫.递归出口---》到哪不可再分

我们发现仅仅剩下一个盘子就不可再分，那麽也就是n==1就是递归出口,把a柱子盘子直接放在c柱子上

n==1–>c.push_back(a.back()); a.pop_back();

三、代码实现

class Solution {
public:void hanota(vector<int>& a, vector<int>& b, vector<int>& c) {dfs(a,a.size(),b,c);}void dfs(vector<int>& a, int n,vector<int>& b, vector<int>& c){if(n==1){c.push_back(a.back());a.pop_back();return;}dfs(a,n-1,c,b);c.push_back(a.back());a.pop_back();dfs(b,n-1,a,c);}
};