正定矩阵的定义:https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459
正定矩阵的作用、验证视频:https://www.bilibili.com/video/BV1Ag411M76G/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
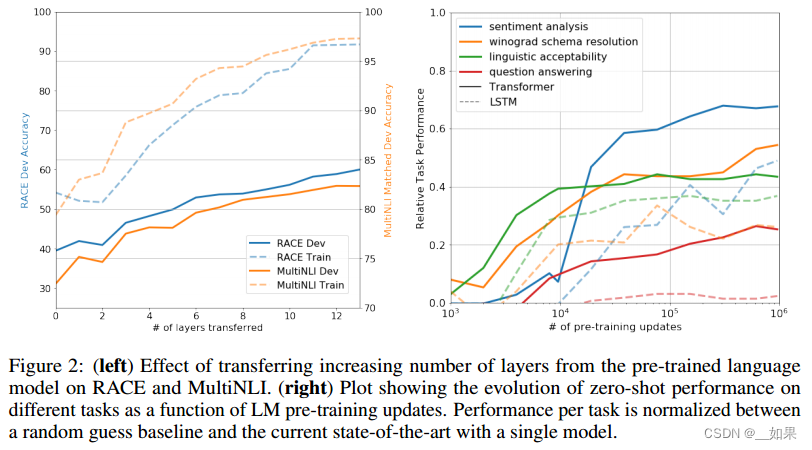
先来看正定矩阵的定义

正定矩阵必须是对称矩阵

第一个问题:为什么需要正定矩阵?正定矩阵的作用是什么?
如下图,任意一个 ”二元二次“ 函数都可以写成 “矩阵运算” 的形式

扩展到 “二次多元” 形式,我们可以写出一个一般形式,如下图
它的一阶导数就是常见的 Ax + b。
它的二阶导就是 A(如果 f(x) 没有前面那个 1/2,那么它的二阶导就是 2A)(二阶导也可以称为 Hessian 矩阵)
如果 矩阵A 是正定的,那么 f(x) 的二阶导就是正定的,此时,f(x) 就是一个严格的下凸函数,拥有唯一全局极小值
二阶导正定是什么意思:(个人直觉) 二阶偏导在所有方向上 > 0


相对的,半正定矩阵的意思是,最小值不唯一

不定矩阵

如下图,面对二次多元函数,如果 A 是正定的,那么要求全局极小值,只需要求一阶偏导 Ax + b =0 的解即可,而这个问题的计算方法和理论是非常丰富的
此外,正定矩阵还可以用来定义一个合理的内积。因为,内积要求任意一个非零向量对自己的内积必须大于 0。而根据正定矩阵的定义,这是恰好满足的,这种性质在 SVM 的核方法里很有用

那么,怎么判断一个矩阵是否是正定矩阵呢?
方法1:从定义出发进行证明,证明对于任意非零向量 x,x^T A x > 0。如下图
但这种方法太复杂,我们几乎不采用

===
方法2:在矩阵A是实对称阵的前提下,计算矩阵 A 的各个特征值,若特征值都大于 0,则矩阵A是正定阵
实际上,A实对称+特征值都大于0 <=> 矩阵A是正定阵。这是一个充分必要条件
我们看看如何证明:
1.证明 A是正定 -> 特征值都大于0:
- 取 x 为特征向量,则 x^T A x = x^T (lamda) x = (lamda) x^T x
- 由于 A正定,所以 x^T A x > 0,也就是说 (lamda) x^T x > 0
- 由于 x^T x > 0,所以 (lamda) >0
- 如此证明了所有特征值 > 0
反过来的证明放下面

2.证明 特征值都大于0 -> A是正定矩阵:
- 若所有特征值都 > 0,那么对于任意向量 x,x^T A x = x^T Q^T (hat) Qx (任意实对称阵可以分解成 正交阵和对角阵 的二次型)
- x^T A x = x^T Q^T (hat) Qx = (Qx)^T (hat) (Qx) 此时我们知道,(hat) 是由矩阵 A 的特征值组成的对角阵,它们都大于 0,那么 (hat) 同时也是一个正定阵,因此 (Qx)^T (hat) (Qx) > 0。所以 x^T A x > 0。
- 证明完毕,A是正定矩阵
这个判别法比较强,因为我们知道特征值了就可以知道很多其它事情,但是,求特征值的计算量比较大,所以这种方法不是我们首选的判别方法
===
方法3:对于实对称阵,若各阶顺序主子式 都大于0 <=> 该矩阵正定 (Sylvester’s Criterion)
(关于这个定理的证明我们先跳过)
这是我们在手算做题时,常用的方法
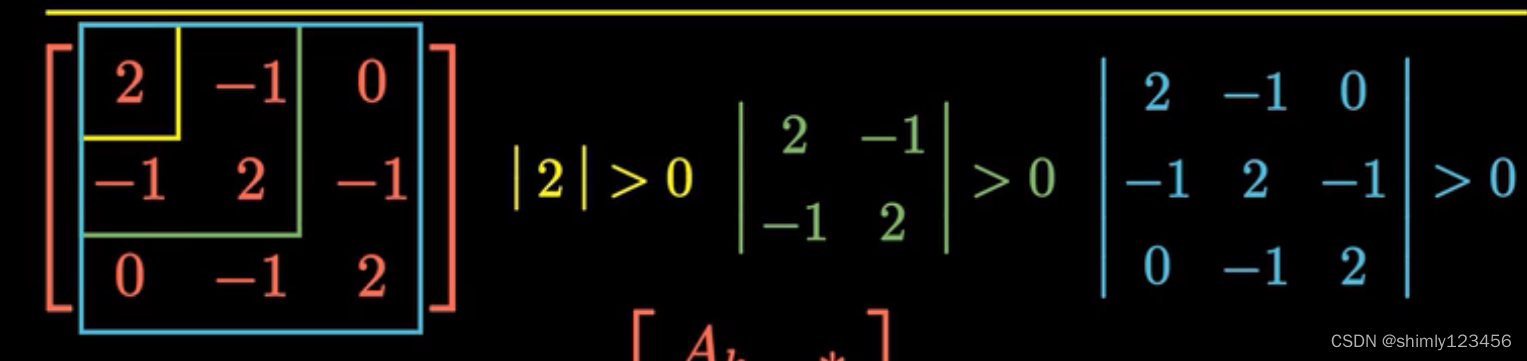
===
方法4:Cholesky 分解
A = R^T R (R 是可逆矩阵) 这个公式是正定阵的一个性质 (证明就 skip 吧,人生苦短)
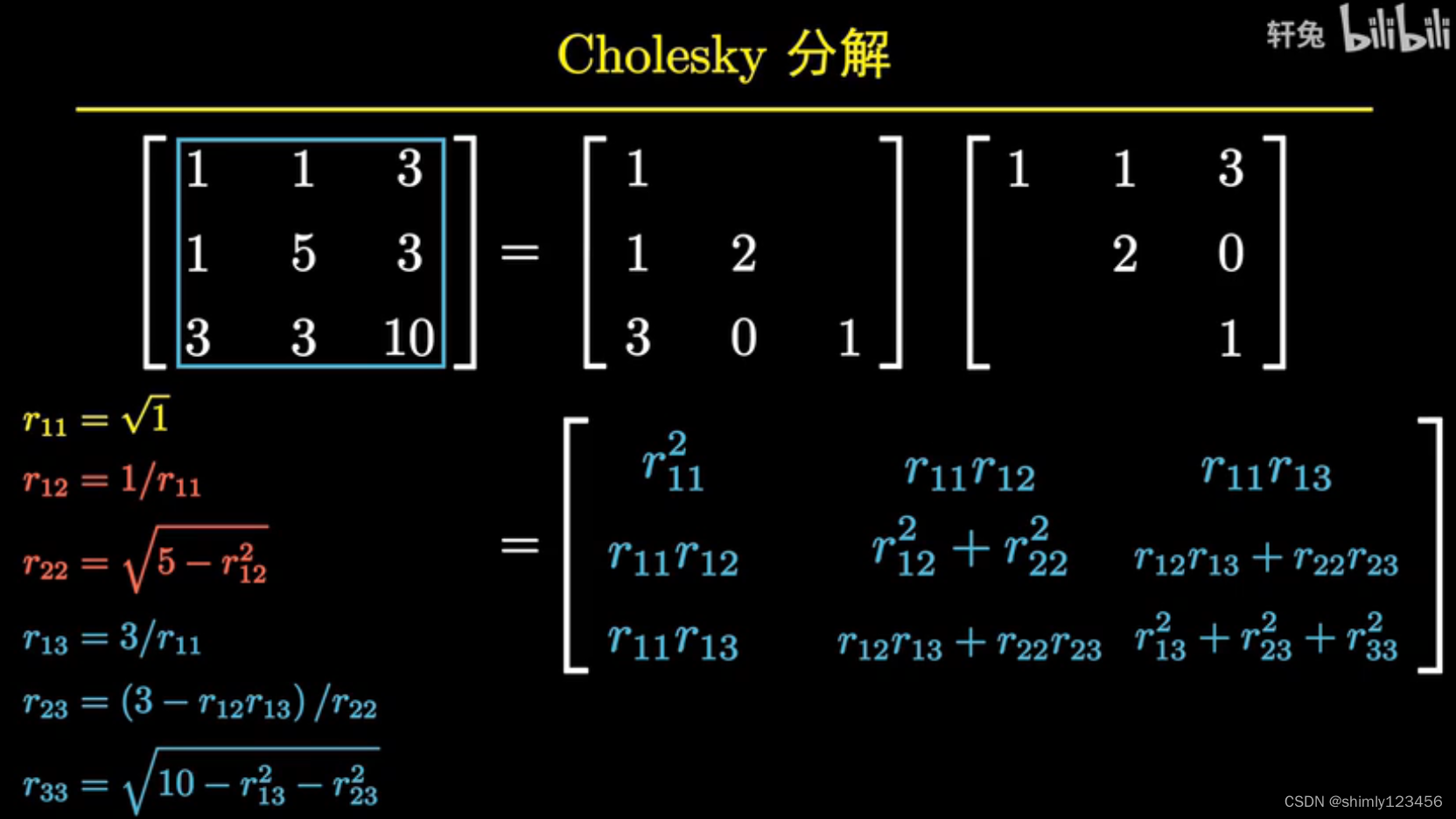
为了让分解出来的 R矩阵 具有唯一性,它需要满足如下图的性质

下图是一个 Cholesky 分解的手算例子
如下图,是用程序进行计算的算法。事件复杂度大约是 n^3/3 的浮点数运算 (在矩阵运算中其实算少的)

如果矩阵不是正定的,可能会在下面两个地方报相应的错误
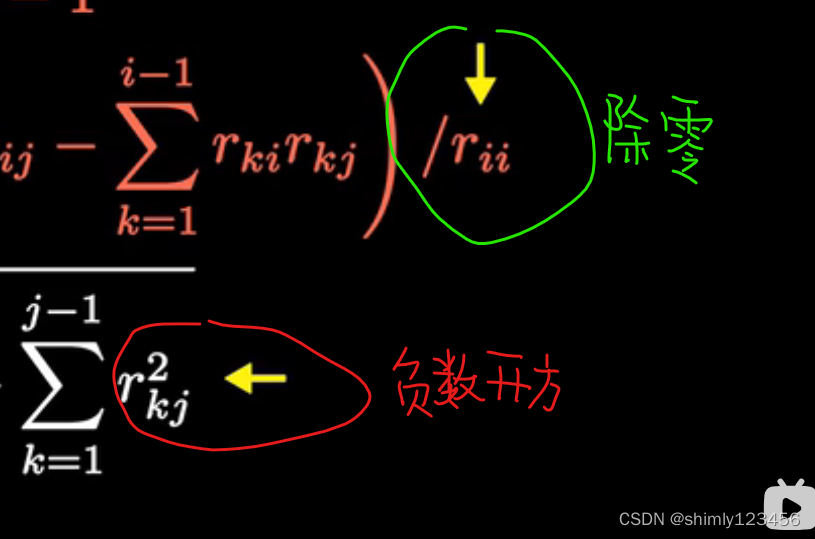
在 MATLAB 中,可以用 chol() 这个命令来得到矩阵A的 cholesky 分解
R = chol(A)
A = R^T R
如果 A 不正定,那么 chol() 就会报错,因此我们可以使用 chol() 判断一个矩阵是否正定
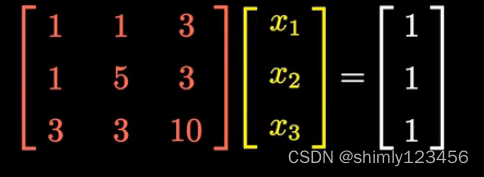
此外,cholesky 分解还可以用来加速解方程组 (面对大型矩阵时有用),比如下图
我们把原来的 Ax = 1 经过分解和换元,得到了 Ry = 1 和 R^T x = y 这两个方程组
虽然方程组数量变多,但是 A 被分解成了上三角和下三角,计算起来方便多了,在大型矩阵中更是如此

正定矩阵还有一个性质,如下图:
证明过程:
- 先把 A 分解成 R^T R (把 R 按照列分块,R^T 按照行分块)
- 那么,aij 的值就是 ri 和 rj 的内积
- 因此,要证明的公式其实就是 ri * rj < ||ri|| * ||rj||
- 这其实就是柯西不等式