k_d树, KNN算法学习笔记_1 距离和范数
二维树中最近邻搜索的示例。这里,树已经构建好了,每个节点对应一个矩形,每个矩形被分割成两个相等的子矩形,叶子对应于包含单个点的矩形
From Wikipedia
1. k k k近邻法是基本且简单的分类与回归方法。 k k k近邻法的基本做法是:对给定的训练实例点和输入实例点,首先确定输入实例点的 k k k个最近邻训练实例点,然后利用这 k k k个训练实例点的类的多数来预测输入实例点的类。
2. k k k近邻模型对应于基于训练数据集对特征空间的一个划分。 k k k近邻法中,当训练集、距离度量、 k k k值及分类决策规则确定后,其结果唯一确定。
3. k k k近邻法三要素:距离度量、 k k k值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。 k k k值小时, k k k近邻模型更复杂; k k k值大时, k k k近邻模型更简单。 k k k值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的 k k k。
常用的分类决策规则是多数表决,对应于经验风险最小化。
4. k k k近邻法的实现需要考虑如何快速搜索k个最近邻点。kd树是一种便于对k维空间中的数据进行快速检索的数据结构。kd树是二叉树,表示对 k k k维空间的一个划分,其每个结点对应于 k k k维空间划分中的一个超矩形区域。利用kd树可以省去对大部分数据点的搜索, 从而减少搜索的计算量。
1.距离度量
在机器学习算法中,我们经常需要计算样本之间的相似度,通常的做法是计算样本之间的距离。
设 x x x和 y y y为两个向量,求它们之间的距离。
这里用Numpy实现,设和为ndarray <numpy.ndarray>,它们的shape都是(N,)
d d d为所求的距离,是个浮点数(float)。
import numpy as np #注意:运行代码时候需要导入NumPy库。
from numpy import linalg as npl
import matplotlib.pyplot as pltnumpy.linalg.norm 文档 Notes
对于ord < 1的值,结果严格来说不是数学上的“范数”,但它仍然可能对各种数值目的有用。
下面的这些范数可以计算:
| ord | 矩阵范数 | 向量范数 | 说明 |
|---|---|---|---|
| ‘fro’ | Frobenius norm | – | Frobenius范数定义为矩阵所有元素的平方和的平方根 |
| ‘nuc’ | nuclear norm | – | 核范数是奇异值的和 |
| inf | max(sum(abs(x), axis=1)) | max(abs(x)) | 绝对值的最大值 |
| -inf | min(sum(abs(x), axis=1)) | min(abs(x)) | 绝对值的最小值 |
| 0 | – | sum(x != 0) | 非零元素的数量 |
| 1 | max(sum(abs(x), axis=0)) | as below | 向量的1范数是绝对值的和 |
| -1 | min(sum(abs(x), axis=0)) | as below | 向量的-1范数是绝对值的最小值 |
| 2 | 2-norm (largest sing. value) | as below | 向量的2范数是奇异值的最大值 |
| -2 | smallest singular value | as below | 向量的-2范数是奇异值的最小值 |
| other | – | sum(abs(x)**ord)**(1./ord) | 其他值的范数, 即: Minkowski范数 |
The Frobenius norm is given by [1]:
∣ ∣ A ∣ ∣ F = [ ∑ i , j a b s ( a i , j ) 2 ] 1 / 2 ||A||_F = [\sum_{i,j} abs(a_{i,j})^2]^{1/2} ∣∣A∣∣F=[i,j∑abs(ai,j)2]1/2
核范数是奇异值的和,即:
∣ ∣ A ∣ ∣ ∗ = ∑ i σ i ( A ) ||A||_* = \sum_i \sigma_i(A) ∣∣A∣∣∗=i∑σi(A)
Frobenius和核范数都只能定义为矩阵,并在x.ndim != 2时引发ValueError。
常见范数[2]
向量范数
| 范数 | 数学表达式 | 描述 | “距离”类型 |
|---|---|---|---|
| 0 范数 | $ |\mathbf{x}|_{0} = #(i \mid x_i \not = 0)$ | 非零向量元素个数之和 | x 到零点的汉明距离 Hamming Distance |
| 1 范数 | ∣ x ∣ 1 = ∑ i ∣ x i ∣ |\mathbf{x}|_{1} = \sum_i \mid x_i \mid ∣x∣1=∑i∣xi∣ | 向量元素绝对值之和 | x 到零点的曼哈顿距离 Manhattan Distance |
| 2 范数 | ∣ x ∣ 2 = ∑ i x i 2 |\mathbf{x}|_{2} = \sqrt{\sum_i x_i^{2}} ∣x∣2=∑ixi2 | 向量元素绝对值的平方和再开方 | x 到零点的欧氏距离 Euclidean Distance |
| p 范数 | ∣ x ∣ p = ∑ i x i p p |\mathbf{x}|_{p} = \sqrt[p]{\sum_i x_i^{p}} ∣x∣p=p∑ixip | 向量元素绝对值的p次方和的1/p次幂 | x 到零点的p阶闵氏距离 Minkowski Distance |
| ∞ \infty ∞ 范数 | ∣ x ∣ ∞ = max ∣ x i ∣ |\mathbf{x}|_{\infty} = \max{ \mid x_i \mid } ∣x∣∞=max∣xi∣ | 所有向量元素绝对值中的最大值 | x 到零点的切比雪夫距离 Chebyshev Distance |
| − ∞ -\infty −∞ 范数 | ∣ x ∣ − ∞ = min ∣ x i ∣ |\mathbf{x}|_{-\infty} = \min{ \mid x_i \mid } ∣x∣−∞=min∣xi∣ | 所有向量元素绝对值中的最小值 | - |
矩阵范数
| 范数 | 数学表达式 | 描述 |
|---|---|---|
| 1 范数 | ∣ A ∣ 1 = max ∑ i ∣ x i , j ∣ |\mathbf{A}|_{1} = \max{ \sum_i \mid x_{i,j} \mid } ∣A∣1=max∑i∣xi,j∣ | 列和范数,即所有矩阵列向量绝对值之和的最大值 |
| 2 范数 | ∣ A ∣ 2 = λ |\mathbf{A}|_{2} = \sqrt{\lambda} ∣A∣2=λ | 谱范数,即 A T A A^TA ATA矩阵的最大特征值的开平方 |
| F 范数 | ∣ A ∣ F = ∑ i ∑ j x i , j 2 |\mathbf{A}|_{F} = \sqrt{ \sum_i \sum_j x_{i,j}^{2} } ∣A∣F=∑i∑jxi,j2 | Frobenius 范数,即矩阵元素绝对值的平方和再开平方 |
| ∞ \infty ∞ 范数 | ∣ A ∣ ∞ = max ∑ j ∣ x i , j ∣ |\mathbf{A}|_{\infty} = \max{ \sum_j \mid x_{i,j} \mid } ∣A∣∞=max∑j∣xi,j∣ | 行和范数,即所有矩阵行向量绝对值之和的最大值 |
| − ∞ -\infty −∞ 范数 | ∣ A ∣ − ∞ = min ∣ x i , j ∣ |\mathbf{A}|_{-\infty} = \min{ \mid x_{i,j} \mid } ∣A∣−∞=min∣xi,j∣ | 所有矩阵元素绝对值中的最小值 |
| 核范数 | ∣ A ∣ ∗ = ∑ i σ i |\mathbf{A}|_{*} = \sum_i \sigma_i ∣A∣∗=∑iσi | 矩阵奇异值之和 |
欧氏距离(Euclidean distance)
欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义,指在 m m m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
距离公式:
d ( x , y ) = ∑ i ( x i − y i ) 2 d\left( x,y \right) = \sqrt{\sum_{i}^{}(x_{i} - y_{i})^{2}} d(x,y)=i∑(xi−yi)2
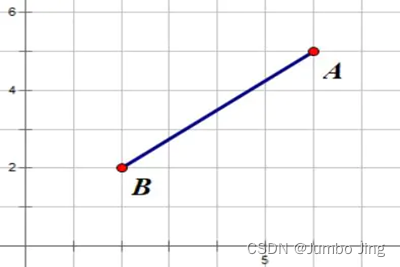
代码实现:
def euclidean(x, y):return np.sqrt(np.sum((x - y)**2))
ndA = np.asanyarray
p1 = ndA((4, 5))
p2 = ndA((12,16))
euDst_ = lambda p1, p2: np.sqrt(np.sum((p1 - p2)**2))
def euDst(p1, p2):return npl.norm(p1 - p2)
曼哈顿距离(Manhattan distance)
想象你在城市道路里,要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源,曼哈顿距离也称为城市街区距离(City Block distance)。
距离公式:
d ( x , y ) = ∑ i ∣ x i − y i ∣ d(x,y) = \sum_{i}^{}|x_{i} - y_{i}| d(x,y)=i∑∣xi−yi∣

代码实现:
def manhattan(x, y):return np.sum(np.abs(x - y))
manDst_ = lambda p1, p2: np.sum(np.abs(p1 - p2))
def manDst(p1, p2):return npl.norm(p1 - p2, ord=1)
切比雪夫距离(Chebyshev distance)
在数学中,切比雪夫距离(Chebyshev distance)或是L∞度量,是向量空间中的一种度量,二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看,切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量,也是超凸度量(injective metric space)的一种。
距离公式:
d ( x , y ) = max i ∣ x i − y i ∣ d\left( x,y \right) = \max_{i}\left| x_{i} - y_{i} \right| d(x,y)=imax∣xi−yi∣

若将国际象棋棋盘放在二维直角座标系中,格子的边长定义为1,座标的 x x x轴及 y y y轴和棋盘方格平行,原点恰落在某一格的中心点,则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离,因此切比雪夫距离也称为棋盘距离。例如位置F6和位置E2的切比雪夫距离为4。任何一个不在棋盘边缘的位置,和周围八个位置的切比雪夫距离都是1。
代码实现:
def chebyshev(x, y):return np.max(np.abs(x - y))
cheDst_ = lambda p1, p2: np.max(np.abs(p1 - p2))
def cheDst(p1, p2):# return np.max(np.abs(p1 - p2))return np.linalg.norm(p1 - p2, ord=np.inf)
闵可夫斯基距离(Minkowski distance)
闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空,为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空间(即假设没有重力,曲率为零的空间)的概念以及表示为特殊距离量的几何学是与狭义相对论的要求相一致的。闵可夫斯基空间不同于牛顿力学的平坦空间。 p p p取1或2时的闵氏距离是最为常用的, p = 2 p= 2 p=2即为欧氏距离,而 p = 1 p =1 p=1时则为曼哈顿距离。
当 p p p取无穷时的极限情况下,可以得到切比雪夫距离。
距离公式:
d ( x , y ) = ( ∑ i ∣ x i − y i ∣ p ) 1 p d\left( x,y \right) = \left( \sum_{i}^{}|x_{i} - y_{i}|^{p} \right)^{\frac{1}{p}} d(x,y)=(i∑∣xi−yi∣p)p1
代码实现:
def minkowski(x, y, ):return np.sum(np.abs(x - y)**p)**(1 / p)
mkDst_ = lambda p1, p2, p: np.sum(np.abs(p1 - p2)**p)**(1 / p)
def mkDst(p1, p2, p):# if p == 1: # 曼哈顿距离# return npl.norm(p1 - p2, ord=1)# elif p == 2: # 欧式距离# return npl.norm(p1 - p2)# elif p == np.inf: # 切比雪夫距离# return npl.norm(p1 - p2, ord=np.inf)# else: # 闵可夫斯基距离return npl.norm(p1 - p2, ord = p) # ?# ord : {non-zero int, inf, -inf, 'fro', 'nuc'}, optional
汉明距离(Hamming distance)
汉明距离是使用在数据传输差错控制编码里面的,汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量,我们以表示两个字,之间的汉明距离。对两个字符串进行异或运算,并统计结果为1的个数,那么这个数就是汉明距离。
距离公式:
d ( x , y ) = 1 N ∑ i 1 x i ≠ y i d\left( x,y \right) = \frac{1}{N}\sum_{i}^{}1_{x_{i} \neq y_{i}} d(x,y)=N1i∑1xi=yi
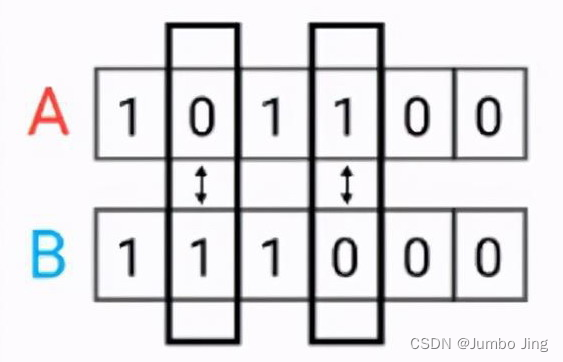
代码实现:
def hamming(x, y):return np.sum(x != y) / len(x)
hmDst_ = lambda p1, p2: np.sum(p1 != p2) / len(p1)
def hmDst(p1, p2):return npl.norm(p1 - p2, ord=0) / len(p1)
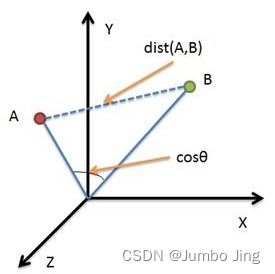
余弦相似度(Cosine Similarity)
余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。这结果是与向量的长度无关的,仅仅与向量的指向方向相关。余弦相似度通常用于正空间,因此给出的值为0到1之间。
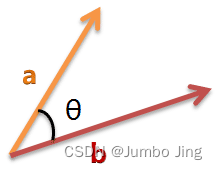
二维空间为例,上图的 a a a和 b b b是两个向量,我们要计算它们的夹角θ。余弦定理告诉我们,可以用下面的公式求得:
cos θ = a 2 + b 2 − c 2 2 a b \cos\theta = \frac{a^{2} + b^{2} - c^{2}}{2ab} cosθ=2aba2+b2−c2
假定 a a a向量是 [ x 1 , y 1 ] \left\lbrack x_{1},y_{1} \right\rbrack [x1,y1], b b b向量是 [ x 2 , y 2 ] \left\lbrack x_{2},y_{2} \right\rbrack [x2,y2],两个向量间的余弦值可以通过使用欧几里得点积公式求出:
cos ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n A i × B i ∑ i = 1 n ( A i ) 2 × ∑ i = 1 n ( B i ) 2 \cos\left( \theta \right) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\sum_{i = 1}^{n}A_{i} \times B_{i}}{\sqrt{\sum_{i = 1}^{n}(A_{i})^{2} \times \sqrt{\sum_{i = 1}^{n}(B_{i})^{2}}}} cos(θ)=∥A∥∥B∥A⋅B=∑i=1n(Ai)2×∑i=1n(Bi)2∑i=1nAi×Bi
cos ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ( x 1 , y 1 ) ⋅ ( x 2 , y 2 ) x 1 2 + y 1 2 × x 2 2 + y 2 2 = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 × x 2 2 + y 2 2 \cos\left( \theta \right) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\left( x_{1},y_{1} \right) \cdot \left( x_{2},y_{2} \right)}{\sqrt{x_{1}^{2} + y_{1}^{2}} \times \sqrt{x_{2}^{2} + y_{2}^{2}}} = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2}} \times \sqrt{x_{2}^{2} + y_{2}^{2}}} cos(θ)=∥A∥∥B∥A⋅B=x12+y12×x22+y22(x1,y1)⋅(x2,y2)=x12+y12×x22+y22x1x2+y1y2
如果向量 a a a和 b b b不是二维而是 n n n维,上述余弦的计算法仍然正确。假定 A A A和 B B B是两个 n n n维向量, A A A是 [ A 1 , A 2 , … , A n ] \left\lbrack A_{1},A_{2},\ldots,A_{n} \right\rbrack [A1,A2,…,An], B B B是 [ B 1 , B 2 , … , B n ] \left\lbrack B_{1},B_{2},\ldots,B_{n} \right\rbrack [B1,B2,…,Bn],则 A A A与 B B B的夹角余弦等于:
cos ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n A i × B i ∑ i = 1 n ( A i ) 2 × ∑ i = 1 n ( B i ) 2 \cos\left( \theta \right) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\sum_{i = 1}^{n}A_{i} \times B_{i}}{\sqrt{\sum_{i = 1}^{n}(A_{i})^{2}} \times \sqrt{\sum_{i = 1}^{n}(B_{i})^{2}}} cos(θ)=∥A∥∥B∥A⋅B=∑i=1n(Ai)2×∑i=1n(Bi)2∑i=1nAi×Bi
代码实现:
from math import *def square_rooted(x):return round(sqrt(sum([a*a for a in x])),3)
def cosine_similarity(x, y):numerator = sum(a * b for a, b in zip(x, y))denominator = square_rooted(x) * square_rooted(y)return round(numerator / float(denominator), 3)
print(cosine_similarity([3, 45, 7, 2], [2, 54, 13, 15]))
cosSm_ = lambda p1, p2:\np.sum(p1 * p2)\/ (np.sqrt(np.sum(p1**2))\* np.sqrt(np.sum(p2**2)))
def cosSm(p1, p2):return npl.norm(p1 - p2, ord=2)\/ (npl.norm(p1, ord=2) * npl.norm(p2, ord=2))
参考
- 黄海广老师的机器学习教程
- 【Numpy】常见范数的数学定义与 Numpy 实现
- 注意⚠️: 本文由vscode的’copilot AI`协助完成, 谨慎使用




![[PyTorch][chapter 9][李宏毅深度学习][CNN]](https://img-blog.csdnimg.cn/direct/ee1281c966204a209c3204c8f2113047.png)




![[排序算法] 如何解决快速排序特殊情况效率低的问题------三路划分](https://img-blog.csdnimg.cn/direct/c5aafbe58f214f3ead0aea4843e5e8f6.png)