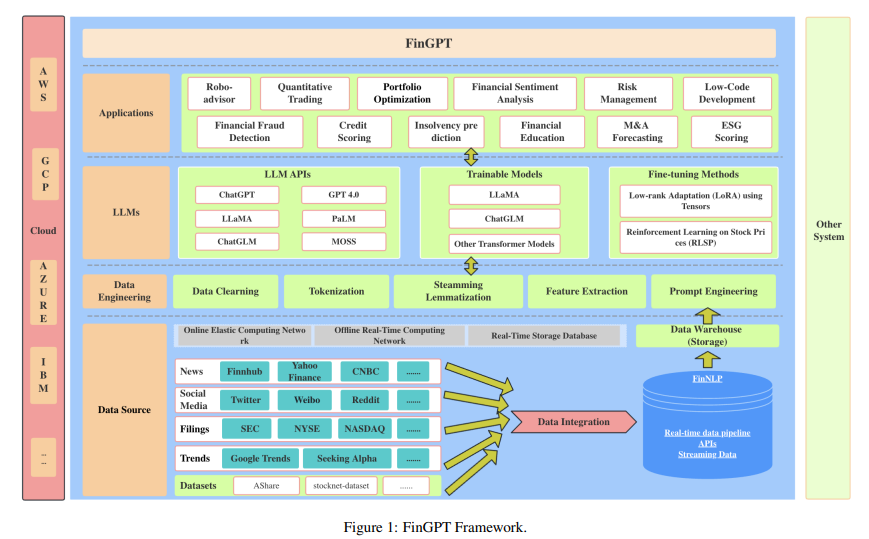
目录
测量分类
测量次数角度
测量条件角度
误差
误差分类
系统误差
随机误差
异常值
误差描述
精密度(Precision)
正确度(Trueness)
准确度/精确度(Accuracy)
随机误差的处理
直接测量
算术平均值与算术平均偏差
标准偏差与高斯分布(正态分布)
例题
间接测量
测量误差的传递
例题
测量结果的表达
有效数字
概念
有效数字的运算法则
数据处理
逐差法
最小二乘法
对比优势
原理
应用
关联系数
测量分类
测量:测量是按照某种规律,用数据来描述观察到的现象,即对事物作出量化描述。
- 社会测量则是指依据一定的规则,将研究对象所具有的属性和特征用一组符号或数字表示出来的一种方法
- 自然科学测量大多运用标准化的仪器或量具,有公认的标准和规则,客观性强。
在机械工程里面,测量指将被测量与具有计量单位的标准量在数值上进行比较,从而确定二者比值的实验认识过程。

测量次数角度
- 直接测量------体重,长度,温度等
- 间接测量------密度,电阻等

测量条件角度
- 等精度测量----------同一条件下重复测量,值不同,但可靠性一样
- 不等精度测量-------不同测量条件(仪器、方法、操作人员等变更),可靠性不同
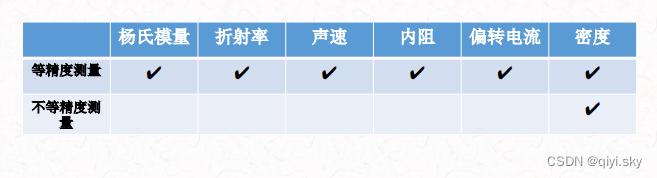
等精度测量:为什么重复测得的值会不一样?
原因:
- 公式的近似性
- 仪器灵敏度和分辨能力局限性
- 环境的不稳定性(动态平衡)
- …
测量值真实值
注意:
- 真实值存在且唯一;
- 测量值不等于真实值,只是近似真实值
误差
误差: 测量结果 与真实值之间的差值
真实值(或称真值):
- 是客观存在的
- 是在一定时间及空间条件下体现事物的真实数值
- 但很难确切表达
测得值是测量所得的结果,记为.
1.绝对误差
2.相对误差
由于真实值是未知的,误差不能确定,
重复测量目的:
- 给出真实值的最佳估计值,
- 估算出此估值的可靠程度
误差分类
前提:同一物理量,相同条件下重复测量。
系统误差
系统误差:保持恒定,或有规律变化;
来源:
- 仪器(未按标准使用)
- 理论公式(近似性、测量方法)
- 测量人员(如时间)
处理方式:修正系统
随机误差
随机误差:时大时小,时正时负,变化无规律
来源:
- 人(感官灵敏度)
- 仪器精度
- 环境条件等
处理方式:分析处理
异常值
异常值(粗大误差、过失误差):明显不符合事实,错的离谱
来源:错误造成
处理方式:剔除
误差描述
精密度(Precision)
重复测量结果的接近程度,
反映偶然误差的大小;

正确度(Trueness)
测量值或实验结果与真值的符合程度,
反映系统误差的大小;

准确度/精确度(Accuracy)
精密度和正确度的综合反映;
若偶然误差小到忽略不计,准确度等于正确度
若系统误差小到忽略不计,准确度等于精密度
随机误差的处理
直接测量
算术平均值与算术平均偏差
- 算术平均值:测量次数足够多时,其代表最佳估算值。
- 算术偏差:各测量值与平均值的偏差
有限次测量时,算术平均偏差常用下式计算:
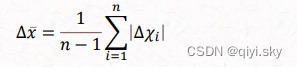
标准偏差与高斯分布(正态分布)
标准偏差: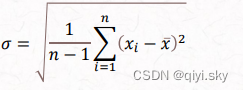
偏差值越大,测量值越分散,随机误差越大;
偏差值越小,测量值越密集,随机误差越小,测量越准确;
算术平均偏差与标准偏差都可以表示测量数据的精密程度,前者计算更简单 (推荐)
两者之间的关系为:![]()
如果测量次数趋于无穷多时,绝对误差的概率呈高斯分别(正态分布)
正态分布特点:对称性、单峰性、有界性、抵偿性
绝对误差概率密度函数:
测量值与平均值之差满足,在(-∞,+∞)必然发生,
![]()
标准差越小,f(0)越大,测量值越聚集
重复测量结果越聚集,测量结果精密度越高;

平均值的标准偏差
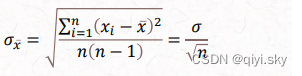
平均值的标准偏差随着测量次数n的增加而减小,即测量次数越多,算术平均值越接近于真实值。
测量次数一般取6~10次
在n>10以后,平均值的标准偏差
变化相当缓慢,测量精度主要还是取决于仪器的精度、测量方法、环境和测量人员等因素,没必要单纯增加测量次数.
例题

间接测量
测量误差的传递
间接测量量一般由一个或多个直接测量量根据公式计算得出,而直接测量量的误差必然会在间接测量量上得到体现,这种影响就是误差传递。
常用间接测量量函数的误差传递公式:

例题

测量结果的表达


有效数字
概念
有效数字:测量结果可靠的加上出现误差的一位
1).有效数字的位数:
从左往右数,以第一个不为零的数字为起点,它左边的“0”不是有效数字,它右边的“0”是有效数字。
![]()
2).取舍法则:
“四舍六入五凑偶”。

3)意义:
有效数字位数的多少,大致反映相对误差的大小。有效位数越多,则相对误差越小,测量结果准确度越高。
![]()
4)有效数字的“0”不可省略
有效数字的运算法则



注意:
有效数字位数取决与测量仪器,而非运算过程。
有效位数越多越精确,但一味追求扩大测量结果的有效位数也是不可取的。
数据处理
数据处理有四种方法:列表法、作图法、逐差法和最小二乘法,这里只展现后两种。
逐差法
逐差法是对等间距测量的有序数据进行逐项或相等间隔项相减得到结果的一种方法。
它计算简便,并可充分利用测量数据,及时发现差错,总结规律,是物理实验中常用的一种数据处理方法。
使用条件:
- 自变量x是等间距离变化的。
- 被测的物理量之间的函数形式可以写成x的多项式,即
使用步骤:

由此可见,与上面一般求平均值方法不同,这时每个数据都用上了。
但应注意,这里的是增加五克砝码时弹簧的平均伸长量。
最小二乘法
对比优势

原理
由一组实验数据找出一条最佳的拟合直线(或曲线),常用的方法是最小二乘法。所得的变量之间的相关函数关系称为回归方程。
所以最小二乘法线性拟合亦称为最小二乘法线性回归。
只讨论用最小二乘法进行一元线性回归问题,
给定函数关系为
目标:计算最小乘数a和b,使各次测量值误差平方和为最小。数学表达式为:

在最佳拟合直线上,各相应点的值与测量值之差的平方和应比在其他的拟合直线上的都要小。
假设
| 函数关系 | |
|---|---|
| 实验数据 | x: y: |
| 目标问题 | 根据实验数据,确定上式中的常数 |
所有测量值都是等精度的。
只要实验中不改变实验条件和方法,这个条件就可以满足。
只有一个变量有明显的随机误差.
因为和
都含有误差,把误差较小的作为变量x,就可满足该条件。Y的误差记为:

应用
对非线性关系,通过适当的变量变换转化成线性问题。需要注意的是,经过变换等精度的限定条件不一定满足。遇到这类情况应采取更恰当的曲线拟合方法。

关联系数
在函数形式确定以后,用回归法处理数据,其结果是唯一的。可见用最小二乘法处理问题的关键是函数形式的选取。为了判断所得结果是否合理,在待定常数确定以后,还需要计算一下相关系数。
对于一元最小二乘法,定义为:
关联系数的数值大小反映了相关程度的好坏。
值介于0和1之间。
值越接近于1,说明实验数据能密集在求得的直线附近,x,y之间存在着线性关系,用线性函数进行回归比较合理;
值越接近于0,说明实验数据对求得的直线很分散,x与y之间不存在线性关系,即用线性回归不妥,必须用其他函数重新试探。
在实验中,一般当时,就认为两个物理量之间存在较密切的线性关系。
END