62.不同路径
力扣题目链接(opens new window)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 2, n = 3
输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
思路
#深搜
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:
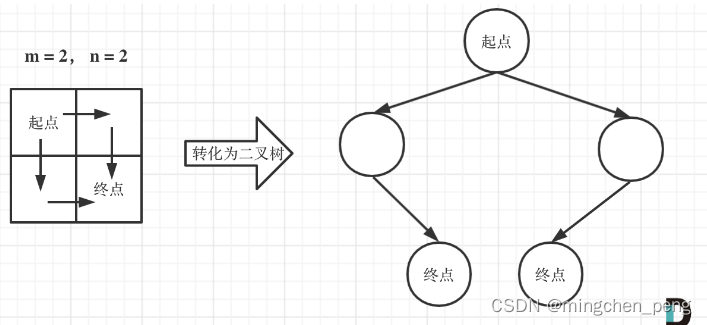
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
private:int dfs(int i, int j, int m, int n) {if (i > m || j > n) return 0; // 越界了if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);}
public:int uniquePaths(int m, int n) {return dfs(1, 1, m, n);}
};
大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
#动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
举例推导dp数组
如图所示:

递归
class Solution:def uniquePaths(self, m: int, n: int) -> int:if m == 1 or n == 1:return 1return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)
动态规划(版本一)
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个二维列表用于存储唯一路径数dp = [[0] * n for _ in range(m)]# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回右下角单元格的唯一路径数return dp[m - 1][n - 1]
动态规划(版本二)
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个一维列表用于存储每列的唯一路径数dp = [1] * n# 计算每个单元格的唯一路径数for j in range(1, m):for i in range(1, n):dp[i] += dp[i - 1]# 返回右下角单元格的唯一路径数return dp[n - 1]
数论
class Solution:def uniquePaths(self, m: int, n: int) -> int:numerator = 1 # 分子denominator = m - 1 # 分母count = m - 1 # 计数器,表示剩余需要计算的乘积项个数t = m + n - 2 # 初始乘积项while count > 0:numerator *= t # 计算乘积项的分子部分t -= 1 # 递减乘积项while denominator != 0 and numerator % denominator == 0:numerator //= denominator # 约简分子denominator -= 1 # 递减分母count -= 1 # 计数器减1,继续下一项的计算return numerator # 返回最终的唯一路径数
63. 不同路径 II
力扣题目链接(opens new window)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?

网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2 解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
向右 -> 向右 -> 向下 -> 向下
向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
思路
这道题相对于62.不同路径 (opens new window)就是有了障碍。
第一次接触这种题目的同学可能会有点懵,这有障碍了,应该怎么算呢?
62.不同路径 (opens new window)中我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了。
动规五部曲:
确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
dp数组如何初始化
在62.不同路径 (opens new window)不同路径中我们给出如下的初始化:
vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
如图:
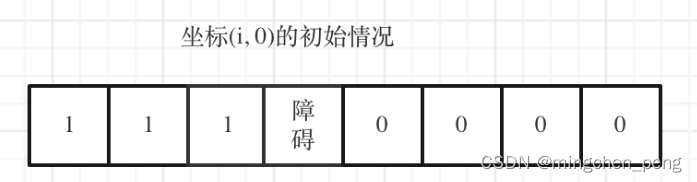
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
vector<vector> dp(m, vector(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}
}
举例推导dp数组
拿示例1来举例如题:
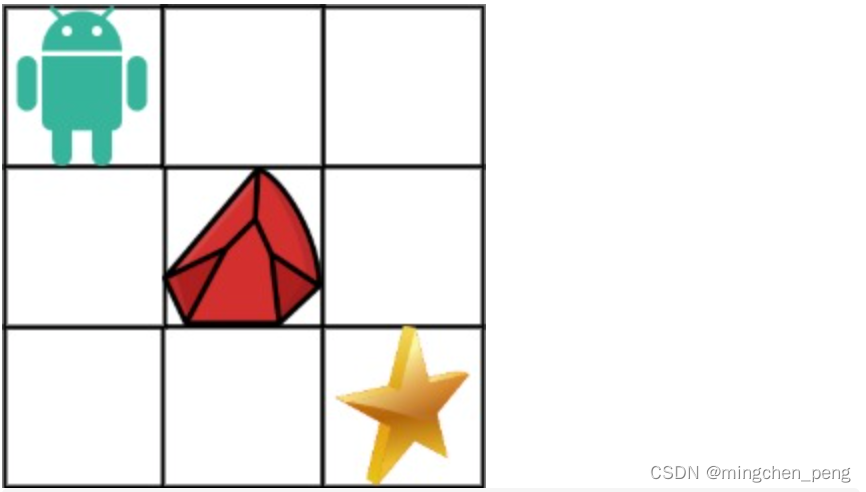
对应的dp table 如图:
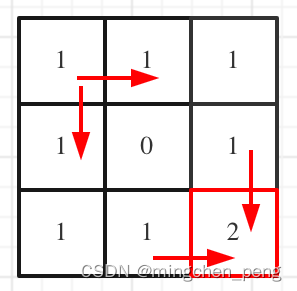
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
动规五部分分析完毕,对应C++代码如下:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};
时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
空间复杂度:O(n × m)
动态规划(版本一)
class Solution:def uniquePathsWithObstacles(self, obstacleGrid):m = len(obstacleGrid)n = len(obstacleGrid[0])if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:return 0dp = [[0] * n for _ in range(m)]for i in range(m):if obstacleGrid[i][0] == 0: # 遇到障碍物时,直接退出循环,后面默认都是0dp[i][0] = 1else:breakfor j in range(n):if obstacleGrid[0][j] == 0:dp[0][j] = 1else:breakfor i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 1:continuedp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m - 1][n - 1]
动态规划(版本二)
class Solution:def uniquePathsWithObstacles(self, obstacleGrid):m = len(obstacleGrid) # 网格的行数n = len(obstacleGrid[0]) # 网格的列数if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:# 如果起点或终点有障碍物,直接返回0return 0dp = [[0] * n for _ in range(m)] # 创建一个二维列表用于存储路径数# 设置起点的路径数为1dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0# 计算第一列的路径数for i in range(1, m):if obstacleGrid[i][0] == 0:dp[i][0] = dp[i - 1][0]# 计算第一行的路径数for j in range(1, n):if obstacleGrid[0][j] == 0:dp[0][j] = dp[0][j - 1]# 计算其他位置的路径数for i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 1:continuedp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m - 1][n - 1] # 返回终点的路径数
动态规划(版本三)
class Solution:def uniquePathsWithObstacles(self, obstacleGrid):if obstacleGrid[0][0] == 1:return 0dp = [0] * len(obstacleGrid[0]) # 创建一个一维列表用于存储路径数# 初始化第一行的路径数for j in range(len(dp)):if obstacleGrid[0][j] == 1:dp[j] = 0elif j == 0:dp[j] = 1else:dp[j] = dp[j - 1]# 计算其他行的路径数for i in range(1, len(obstacleGrid)):for j in range(len(dp)):if obstacleGrid[i][j] == 1:dp[j] = 0elif j != 0:dp[j] = dp[j] + dp[j - 1]return dp[-1] # 返回最后一个元素,即终点的路径数
动态规划(版本四)
class Solution:def uniquePathsWithObstacles(self, obstacleGrid):if obstacleGrid[0][0] == 1:return 0m, n = len(obstacleGrid), len(obstacleGrid[0])dp = [0] * n # 创建一个一维列表用于存储路径数# 初始化第一行的路径数for j in range(n):if obstacleGrid[0][j] == 1:breakdp[j] = 1# 计算其他行的路径数for i in range(1, m):if obstacleGrid[i][0] == 1:dp[0] = 0for j in range(1, n):if obstacleGrid[i][j] == 1:dp[j] = 0else:dp[j] += dp[j - 1]return dp[-1] # 返回最后一个元素,即终点的路径数
动态规划(版本五)
class Solution:def uniquePathsWithObstacles(self, obstacleGrid):if obstacleGrid[0][0] == 1:return 0m, n = len(obstacleGrid), len(obstacleGrid[0])dp = [0] * n # 创建一个一维列表用于存储路径数# 初始化第一行的路径数for j in range(n):if obstacleGrid[0][j] == 1:breakdp[j] = 1# 计算其他行的路径数for i in range(1, m):if obstacleGrid[i][0] == 1:dp[0] = 0for j in range(1, n):if obstacleGrid[i][j] == 1:dp[j] = 0continuedp[j] += dp[j - 1]return dp[-1] # 返回最后一个元素,即终点的路径数
343. 整数拆分
力扣题目链接(opens new window)
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
思路
看到这道题目,都会想拆成两个呢,还是三个呢,还是四个…
我们来看一下如何使用动规来解决。
#动态规划
动规五部曲,分析如下:
确定dp数组(dp table)以及下标的含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
dp[i]的定义将贯彻整个解题过程,下面哪一步想不懂了,就想想dp[i]究竟表示的是啥!
确定递推公式
可以想 dp[i]最大乘积是怎么得到的呢?
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
那有同学问了,j怎么就不拆分呢?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。
所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
那么在取最大值的时候,为什么还要比较dp[i]呢?
因为在递推公式推导的过程中,每次计算dp[i],取最大的而已。
dp的初始化
不少同学应该疑惑,dp[0] dp[1]应该初始化多少呢?
有的题解里会给出dp[0] = 1,dp[1] = 1的初始化,但解释比较牵强,主要还是因为这么初始化可以把题目过了。
严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
拆分0和拆分1的最大乘积是多少?
这是无解的。
这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1,这个没有任何异议!
确定遍历顺序
确定遍历顺序,先来看看递归公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
所以遍历顺序为:
for (int i = 3; i <= n ; i++) {for (int j = 1; j < i - 1; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}
注意 枚举j的时候,是从1开始的。从0开始的话,那么让拆分一个数拆个0,求最大乘积就没有意义了。
j的结束条件是 j < i - 1 ,其实 j < i 也是可以的,不过可以节省一步,例如让j = i - 1,的话,其实在 j = 1的时候,这一步就已经拆出来了,重复计算,所以 j < i - 1
至于 i是从3开始,这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。
更优化一步,可以这样:
for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}
因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 * 3, 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。
只不过我们不知道m究竟是多少而已,但可以明确的是m一定大于等于2,既然m大于等于2,也就是 最差也应该是拆成两个相同的 可能是最大值。
那么 j 遍历,只需要遍历到 n/2 就可以,后面就没有必要遍历了,一定不是最大值。
至于 “拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的” 这个我就不去做数学证明了,感兴趣的同学,可以自己证明。
举例推导dp数组
举例当n为10 的时候,dp数组里的数值,如下:
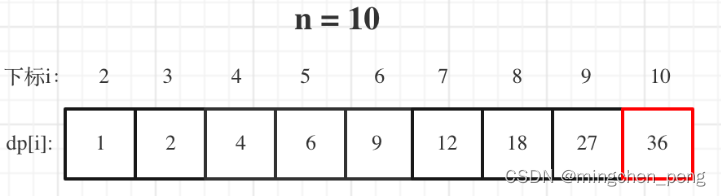
以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};
时间复杂度:O(n^2)
空间复杂度:O(n)
#贪心
本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
我没有证明,而是直接用了结论。感兴趣的同学可以自己再去研究研究数学证明哈。
给出我的C++代码如下:
class Solution {
public:int integerBreak(int n) {if (n == 2) return 1;if (n == 3) return 2;if (n == 4) return 4;int result = 1;while (n > 4) {result *= 3;n -= 3;}result *= n;return result;}
};
时间复杂度:O(n)
空间复杂度:O(1)
#总结
总结
本题掌握其动规的方法,就可以了,贪心的解法确实简单,但需要有数学证明,如果能自圆其说也是可以的。
其实这道题目的递推公式并不好想,而且初始化的地方也很有讲究,我在写本题的时候一开始写的代码是这样的:
class Solution {
public:int integerBreak(int n) {if (n <= 3) return 1 * (n - 1);vector<int> dp(n + 1, 0);dp[1] = 1;dp[2] = 2;dp[3] = 3;for (int i = 4; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], dp[i - j] * dp[j]);}}return dp[n];}
};
这个代码也是可以过的!
在解释递推公式的时候,也可以解释通,dp[i] 就等于 拆解i - j的最大乘积 * 拆解j的最大乘积。 看起来没毛病!
但是在解释初始化的时候,就发现自相矛盾了,dp[1]为什么一定是1呢?根据dp[i]的定义,dp[2]也不应该是2啊。
但如果递归公式是 dp[i] = max(dp[i], dp[i - j] * dp[j]);,就一定要这么初始化。递推公式没毛病,但初始化解释不通!
虽然代码在初始位置有一个判断if (n <= 3) return 1 * (n - 1);,保证n<=3 结果是正确的,但代码后面又要给dp[1]赋值1 和 dp[2] 赋值 2,这其实就是自相矛盾的代码,违背了dp[i]的定义!
我举这个例子,其实就说做题的严谨性,上面这个代码也可以AC,大体上一看好像也没有毛病,递推公式也说得过去,但是仅仅是恰巧过了而已。
动态规划(版本一)
class Solution:# 假设对正整数 i 拆分出的第一个正整数是 j(1 <= j < i),则有以下两种方案:# 1) 将 i 拆分成 j 和 i−j 的和,且 i−j 不再拆分成多个正整数,此时的乘积是 j * (i-j)# 2) 将 i 拆分成 j 和 i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是 j * dp[i-j]def integerBreak(self, n):dp = [0] * (n + 1) # 创建一个大小为n+1的数组来存储计算结果dp[2] = 1 # 初始化dp[2]为1,因为当n=2时,只有一个切割方式1+1=2,乘积为1# 从3开始计算,直到nfor i in range(3, n + 1):# 遍历所有可能的切割点for j in range(1, i // 2 + 1):# 计算切割点j和剩余部分(i-j)的乘积,并与之前的结果进行比较取较大值dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)return dp[n] # 返回最终的计算结果
动态规划(版本二)
class Solution:def integerBreak(self, n):if n <= 3:return 1 * (n - 1) # 对于n小于等于3的情况,返回1 * (n - 1)dp = [0] * (n + 1) # 创建一个大小为n+1的数组来存储最大乘积结果dp[1] = 1 # 当n等于1时,最大乘积为1dp[2] = 2 # 当n等于2时,最大乘积为2dp[3] = 3 # 当n等于3时,最大乘积为3# 从4开始计算,直到nfor i in range(4, n + 1):# 遍历所有可能的切割点for j in range(1, i // 2 + 1):# 计算切割点j和剩余部分(i - j)的乘积,并与之前的结果进行比较取较大值dp[i] = max(dp[i], dp[i - j] * dp[j])return dp[n] # 返回整数拆分的最大乘积结果
贪心
class Solution:def integerBreak(self, n):if n == 2: # 当n等于2时,只有一种拆分方式:1+1=2,乘积为1return 1if n == 3: # 当n等于3时,只有一种拆分方式:1+1+1=3,乘积为1return 2if n == 4: # 当n等于4时,有两种拆分方式:2+2=4和1+1+1+1=4,乘积都为4return 4result = 1while n > 4:result *= 3 # 每次乘以3,因为3的乘积比其他数字更大n -= 3 # 每次减去3result *= n # 将剩余的n乘以最后的结果return result