题目背景:目前往往需要对测序后的序列进行聚类与比对。其中聚类指的是将测序序列聚类以判断原始序列有多少条,聚类后相同类的序列定义为一个簇。比对则是指在聚类基础上对一个簇内的序列进行比对进而输出一条最有 可能的正确序列。通过聚类与比对将会极大地恢复原始序列的信息,但需要注意 由于DNA测序后序列众多,如何高效地进行聚类与比对则是在满足准确率基础上的另一大难点。

数据说明:
“train_reference.txt”是某次合成的目标序列,其中第一行为序号,第二行
为序列内容。
通过真实合成、测序后读取到的测序序列文件为“train_reads.txt”,我们已经对测序序列进行了分类,该文件第一行为目标序列的序号,第二行为序列内容。
基于赛题提供的数据,自主查阅资料,选择合适的方法完成如下任务:
任务1:观察数据集“train_reads.txt”、“train_reference.txt”,针对这次合成任务,进行错误率(插入、删除、替换、断链)、拷贝数方面的分析。其中错误率定义为某个碱基发生错误的概率,需要对不同类型的错误率分别进行分析。拷贝数定义为原始序列复制的数量。
·数据读取与查看:
首先需要根据题目给出的数据信息,对任务1中提到的两个数据集“train_reads.txt”、“train_reference.txt”进行读取与查看。
这里我们采用python语言,Jupiter notebook编程:
import pandas as pd
import numpy as np
#1#读取数据
df_reference = pd.read_csv('train_reference.txt', delimiter=' ',header=None)
df_reference.columns = ['序号', '序列内容'] # 替换列名
df_reference
df_train=pd.read_csv('train_reads.txt',delimiter=' ',header=None)
df_train.columns = ['序号', '序列内容'] # 替换列名
df_train·拷贝数分析:
由于拷贝数的统计计算较为简单,我们首先对拷贝数进行统计分析。
根据题意,拷贝数定义为原始序列复制的数量,所以我们只需要计算每个序列对应的复制次数。
代码如下:
#拷贝数分析
df_copies=df_train['序号'].value_counts().sort_index()
df_copies
#可视化
import matplotlib.pyplot as plt
# 绘制柱状图
plt.bar(df_copies.index, df_copies.values)
plt.xlabel('Order')
plt.ylabel('Count')
plt.title('Order Counts')
plt.show()从可视化结果可以直观地看出,绝大多数序列被复制的次数都在100-140之间,但是具体的复制数目参差不齐。
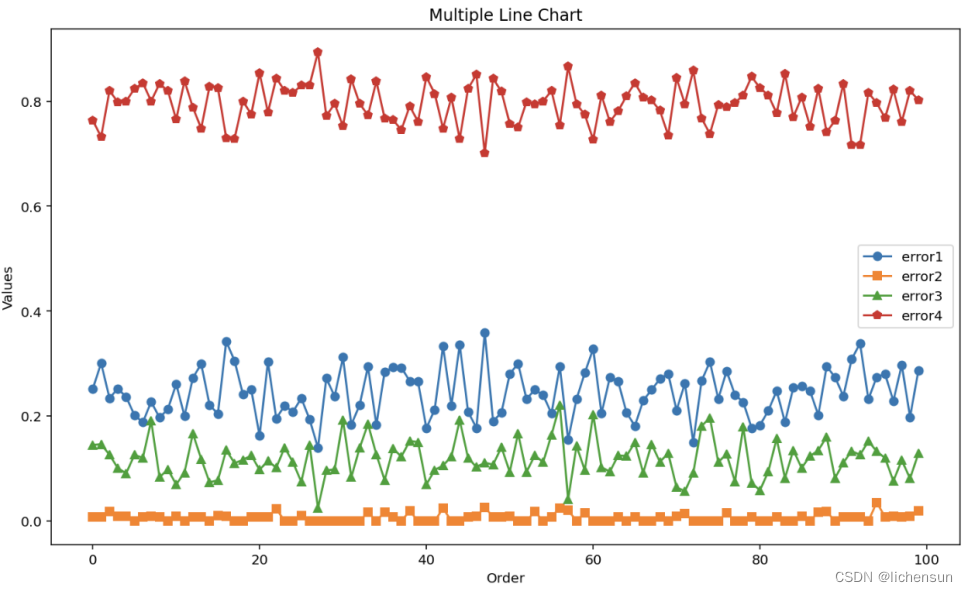
·错误率分析:
错误率共有四种类型:(插入、删除、替换、断链)
针对每种类型,需要我们进行人工定义相应的错误率计算方式:
- 插入错误(记为1类错误)
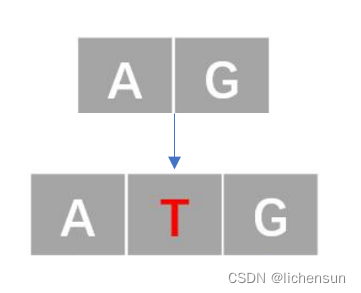
- 删除错误(记为2类错误)
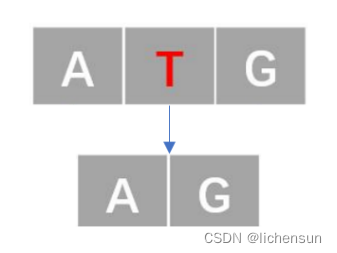
- 替换错误(记为3类错误)

-
断链(记为4类错误)
-
该类错误比较特殊,在 DNA 复制过程中,"断链"通常指的是 DNA 双螺旋的某一条链在复制时发生了断裂,形成一个或多个暂时的单链断裂。这个过程可能是由于复制过程中的各种因素引起的。
比较直观的观测方法是查看复制链的长度,如果序列长度比原定目标长度少了25%及以上,可以认为发生了断链。
如发生断链,4类错误率记为100%(1),否则记为0。
要统计从字符串 B 修改到字符串 A 所涉及的添加、删除和替换的字符个数,可以使用编辑距离(Levenshtein 距离)的概念。编辑距离是衡量两个字符串相似程度的一种方法,包括插入、删除和替换的操作。
在 Python 中,可以使用第三方库 python-Levenshtein 来计算编辑距离。
import Levenshtein
#实现代码请戳完整版获取
任务 2:设计开发一种模型用于对测序后的序列“train_reads.txt”进行聚类,
并根据“train_reads.txt”的标签验证模型准确性。模型主要从两方面评估效果:
-
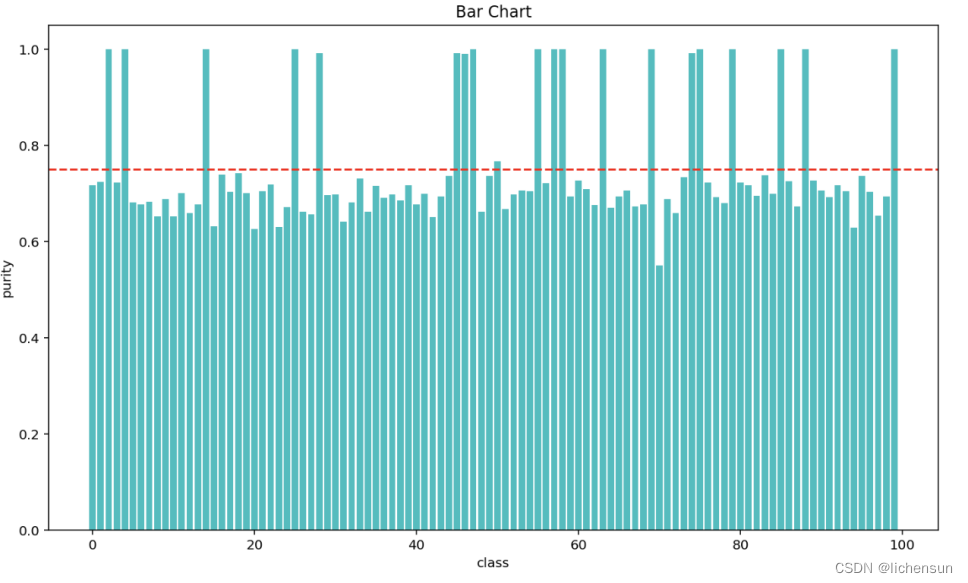
聚类后准确性(包括簇的数量以及簇内纯度)、(2)聚类速度(以分钟为单位)
思路提示:标签即为文件第一行——目标序列的序号,在该任务中,我们将假设序号未知,尝试通过聚类的方法来标记各复制得到的序列可能对应哪个目标序列。
对测序后的序列进行聚类,聚类的依据即为与序列之间的相似性。
聚类是一种将相似的数据点分组的方法。在字符串的情境下,可以使用字符串之间的相似度来聚类。以下是一个示例,使用 KMeans 聚类算法进行字符串的聚类:
#代码见完整版任务 3:“test_reads.txt”是我们在另一种合成环境下合成的测序文件(与“train_reads.txt”的目标序列不相同),请用任务 2 所开发的模型对其进行聚类,给出聚类耗时以及“test_reads.txt”的目标序列数量,给出拷贝数分布图。
由于test数据不清楚分几类合适,需要进行初步的分类步长探索。这里通过设置合理的取样步长采用遍历方法,每次遍历直接套用任务2中设计好的模型(即k-means聚类方法)即可。
对于分类探索,根据实际问题背景,对每个目标序列进行的拷贝数目应该大致相同。
任务 4:聚类后能否通过比对恢复原始信息也是极为关键的,设计开发一种用于同簇序列的比对模型,该模型可以针对同簇的DNA序列进行比对并输出最有可能正确的目标序列。 请使用该工具对任务 3 中“test_reads.txt”的聚类后序列进行比对,并输出“test_reads.txt”最有可能的目标序列,并分析“test_reads.txt”的错误率。(请用一个“test_ref.txt”的文件记录“test_reads.txt”的目标序列。
观察已知数据,不难发现目标序列长度为60.
思路1:针对每个簇内的复制序列,通过相似度计算找出其中最可能与目标序列接近程度最大的序列。依据其他序列修正为长度60作为预测目标序列。
思路2:将每个簇内的复制序列进行长度切割,分别找出各片段的高频序列,将其拼接得到预测的目标序列。
思路3:直接计算公共相同片段(前缀、后缀等),将其适当拼接。
为了构造一个新字符串,使其尽可能与已知的10个字符串都具有很大的相似度,你可以考虑找到这些字符串之间的最长公共子串(Longest Common Substring)。以下是一个示例,使用动态规划来找到最长公共子串,并构造新字符串:
def longest_common_substring(str1, str2):
m, n = len(str1), len(str2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
max_len = 0
end_index = 0
for i in range(1, m + 1):
for j in range(1, n + 1):
if str1[i - 1] == str2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
if dp[i][j] > max_len:
max_len = dp[i][j]
end_index = i - 1
else:
dp[i][j] = 0
return str1[end_index - max_len + 1:end_index + 1]
def construct_string(known_strings):
common_substring = known_strings[0]
for i in range(1, len(known_strings)):
common_substring = longest_common_substring(common_substring, known_strings[i])
# 构造新字符串,将最长公共子串重复若干次
constructed_string = common_substring * 5 # 假设构造的字符串长度为5倍最长公共子串长度
return constructed_string
# 示例
known_strings = ["apple", "apricot", "appetizer", "apology", "apex", "applause", "apricot", "april", "apocalypse", "apostrophe"]
constructed_string = construct_string(known_strings)
print(f"构造的字符串: {constructed_string}")
在这个示例中,longest_common_substring 函数用于找到两个字符串的最长公共子串,然后 construct_string 函数使用这个方法找到所有字符串的最长公共子串,并将其重复若干次以构造新字符串。请注意,具体的重复次数和其他参数可能需要根据实际情况进行调整。
在获得预测的目标序列后,继续采用task1中的方法进行错误率分析即可。
完整获取请戳↓
baiduwangpan:https://pan.baidu.com/s/1BKsSgjSSnHu4433O7jf06w?pwd=ggt9 提取码:ggt9