目录
初等变换求逆矩阵
矩阵乘法
求矩阵方程
求线性方程组
解齐次线性方程组
带有未知数的方程组
初等变换求逆矩阵
如果,则A可逆,且
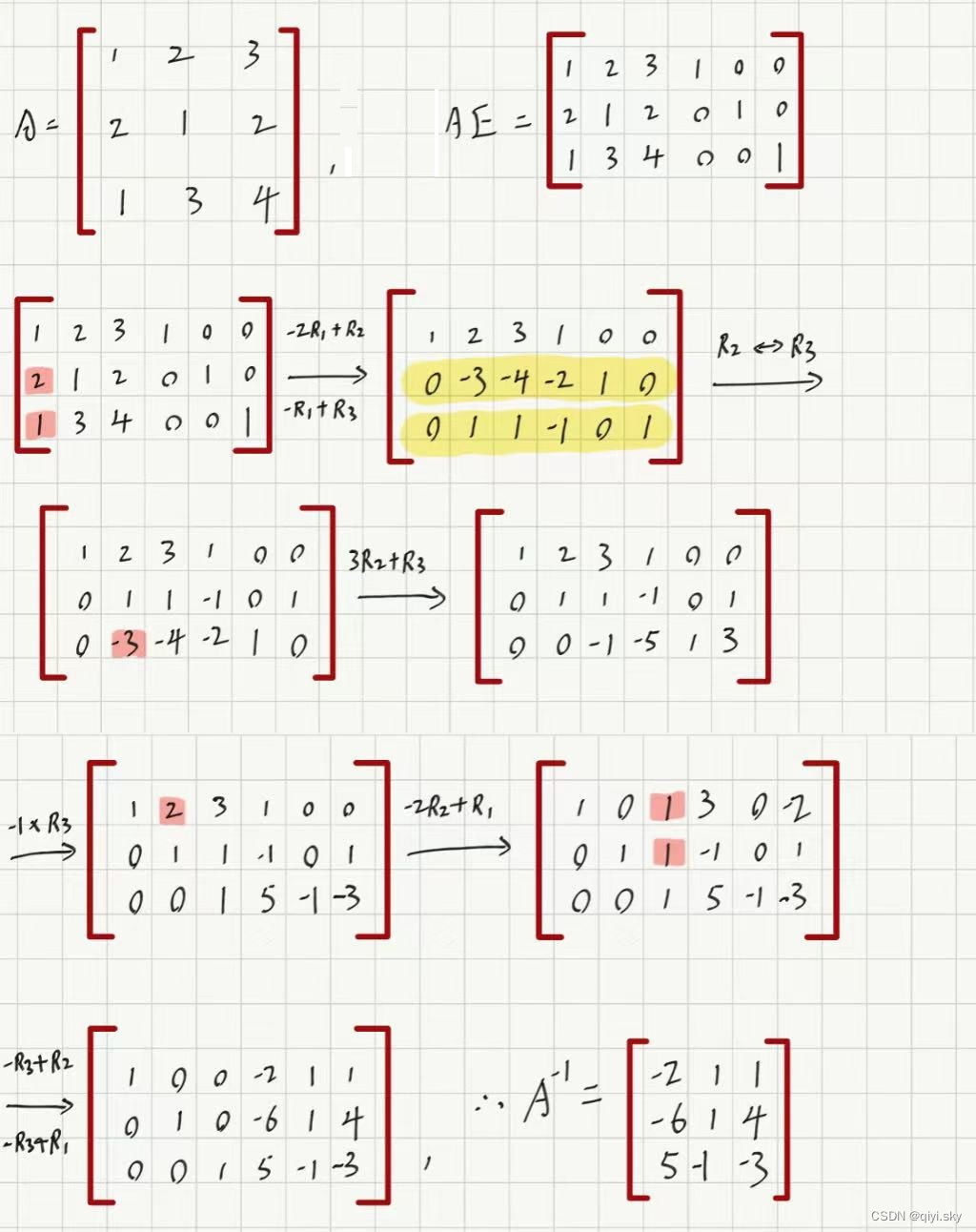
例题:
,求A的逆矩阵。
矩阵乘法
求AB,BA.
矩阵之间的乘法是行乘以列,以这道题为例,具体地说,
相乘的结果矩阵 第一行第一列的数,等于第一个矩阵第一行的所有数对应乘第二个矩阵的第一列的所有数并相加;
相乘的结果矩阵 第一行第二列的数,等于第一个矩阵第一行的所有数对应乘第二个矩阵的第二列的所有数并相加;
相乘的结果矩阵 第二行第一列的数,等于第一个矩阵第二行的所有数对应乘第二个矩阵的第一列的所有数并相加;
相乘的结果矩阵 第二行第二列的数,等于第一个矩阵第二行的所有数对应乘第二个矩阵的第二列的所有数并相加;
也就是:
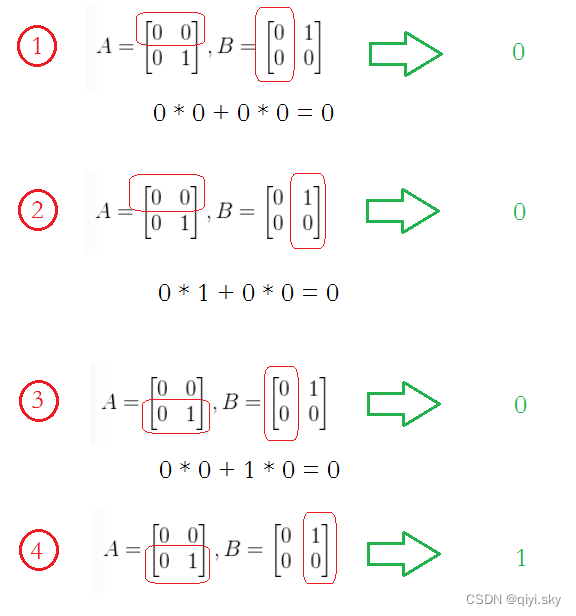
故而易求得 :
可以练习下面这道题重新感受一下:
,求AB。
答案:
求矩阵方程
,
,求x.
首先可以把x移到等式左边,
按照正常解方程的思维,我们会把x提出来,如下所示,
但是A是矩阵,矩阵不能与一个常数进行加减的运算,于是乘以单位矩阵E。
这样才是正确的形式,然后我们再来判断是否可逆,也就是算它的行列式的值:
所以可逆,这时我们给等式两边同时左乘
,
也就是乘以的逆,左乘的顺序不能换,根据性质可知,可逆的矩阵乘以自身的逆矩阵等于单位矩阵E,得:
矩阵A已知,计算出结果即可。
再来看另一道类似的题目:
已知矩阵方程,其中
,求x.
由,将x与E对调,提出x,得:
而可逆,
故可得:
求线性方程组
先将线性方程组写成矩阵形式,然后求解。
矩阵形式:
然后对该矩阵作初等变换,将虚线左边的矩阵变换为单位矩阵, 可得:
原方程组与该矩阵对应的方程组同解,于是:
另一种写法:
将方程组写成矩阵方程:
即,
因为,故
存在,所以:
解齐次线性方程组
判断齐次线性方程组
的解的情况,并求其非零解.(有非零解的充要条件是系数矩阵的行列式的值为零)
讲方法,先将该齐次线性方程组的系数矩阵写出来:
经过一通初等变换,得到它的标准式(最重要的、不能计算出错的一步):
所以A的秩为2,(矩阵的秩小于未知数的量为无穷解,等于未知数的量时有唯一解,大于未知数的量则为无解)
所以有无穷个解,且为自由变量,设
即通解为,
也可写作:
当时,得非零解。
带有未知数的方程组
当k为何值时,方程组
有解或无解?在方程组有解时,求出方程组的解.
对方程组的增广矩阵进行初等变换:
当时,即
时方程组无解;
当时方程组有解,继续进行初等变换,得:
化为标准式:
解得:
END