6.1 点估计问题概述

一、点估计的概念

二、评价估计量的标准

1. 无偏性

• 定义1：设^ θ(X1,…,Xn)是未知参数θ的估计量，若E(^ θ)=θ,则称^θ为θ的无偏估计量
• 定理1：设X1,…,Xn,为取自总体X的样本，总体X的均值为μ，方差为σ²,则
  (I)样本均值¯X是μ的无偏估计量；
  (2)样本方差S²是σ²的无偏估计量；
  
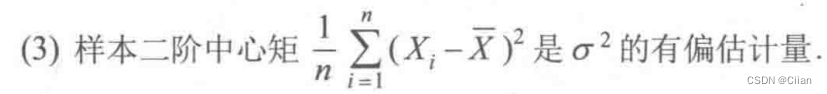
  &1
  
  

2. 有效性
   无偏性是有效性的前提。

• 定义2：
  
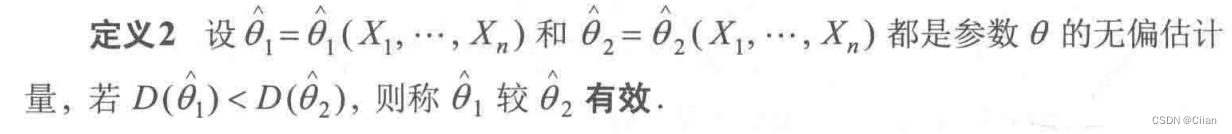
• 例题：
  
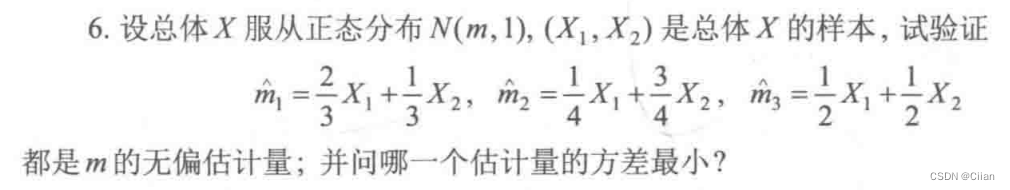
  *1

3. 相合性（一致性）
   我们不仅希望一个估计量是无偏的，并且具有较小的方差，还希望当样本容量无限增大时，估计量能在某种意义下任意接近未知参数的真值，由此引入相合性（一致性)的评价标准.
   

6.2 点估计的常用方法

一、矩估计法

**矩估计法的基本思想是用样本矩估计总体矩.**由大数定律知，当总体的k阶矩存在时，样本的k阶矩依概率收敛于总体的k阶矩.例如，可用样本均值X作为总体均值E(X)的估计量.一般地，记

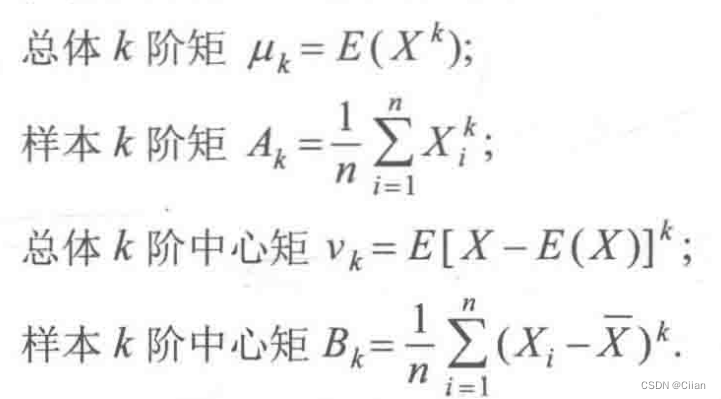
• 总体k阶矩=总体k阶原点矩
  

• 定义1：用相应的样本矩去估计总体矩的方法称为矩估计法.用矩估计法确定的估计量称为矩估计量.相应的估计值称为矩估计值，矩估计量与矩估计值统称为矩估计.

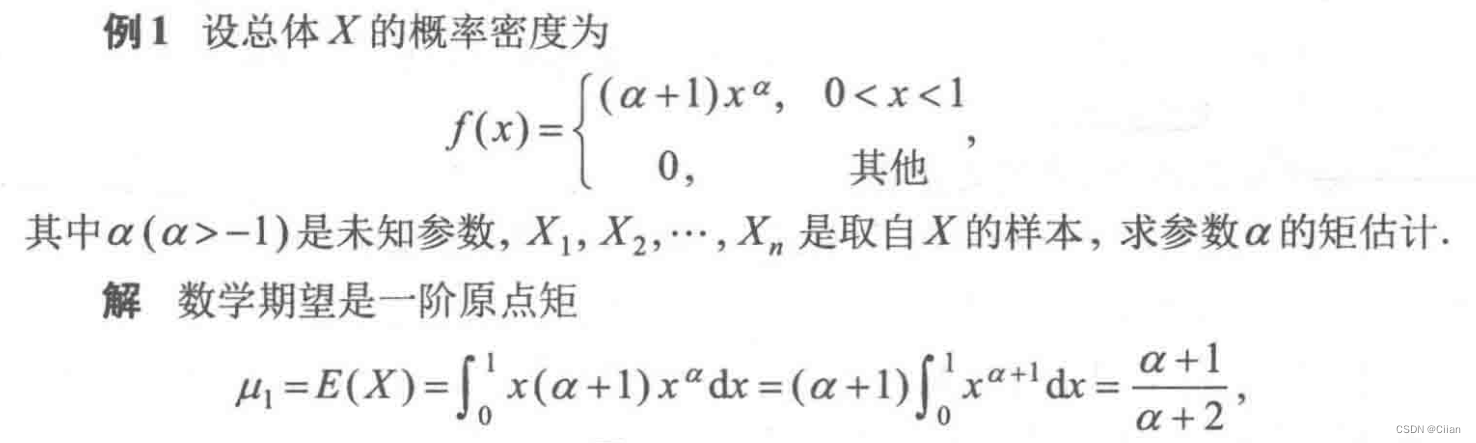
令¯X=E(X)，则

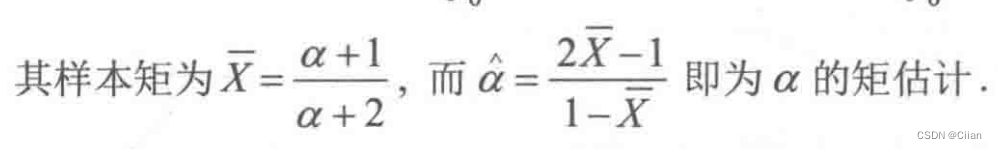
2.

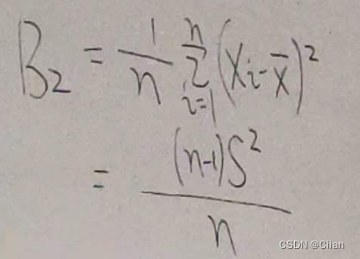
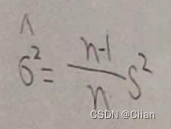
令¯X=E(X)，则¯X=3-2θ
则矩估计量^θ=(3-¯X)/2，
矩估计值 ^θ=

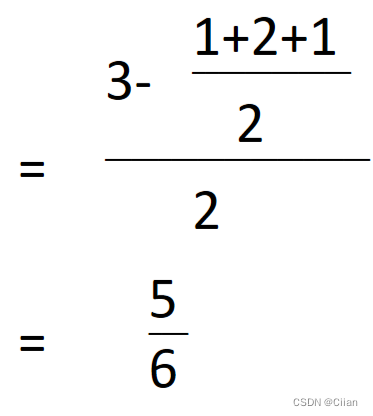
先求矩估计量，再求矩估计值。

二、最大似然（可能）估计法

1.最大似然估计法的基本思想

• 似然函数
  
  即求概率
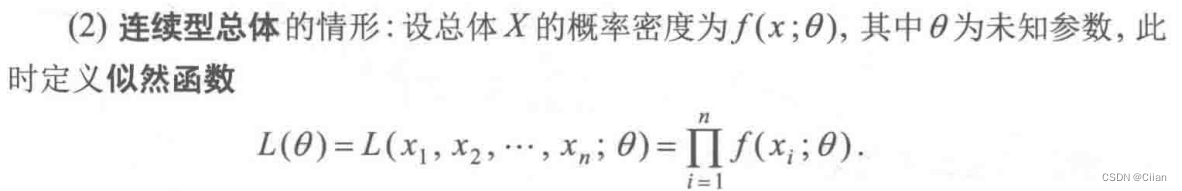  =fx₁(x₁)*fx₂(x₂) *… *fx_n(x_n)
  即求联合密度函数的函数值

似然函数L(θ)的值的大小意味着该样本值出现的可能性的大小，在已得到样本值x1,x2,…,xn的情况下，则应该选择使L(θ)达到最大值的那个θ作为θ的估计^θ.这种求点估计的方法称为最大似然估计法.
求最大似然估计值，再求最大似然估计量

• 定义2：最大似然估计值，最大似然估计量，最大似然估计
  
  

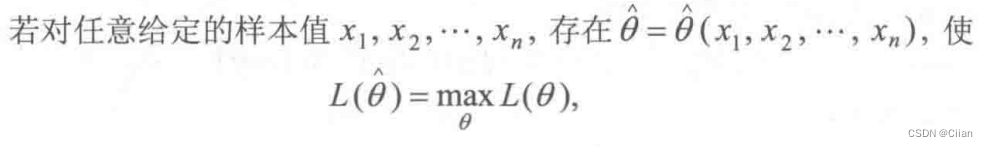
• （离散型）例4：设X ~b(1,p),X1,X2,Xn是取自总体X的一个样本，试求参数p的最大似然估计.
  

• （连续型）例5：设总体X服从指数分布，其概率密度函数为
  

置信区间

一、置信区间的概念

定义1设θ为总体分布的未知参数，X₁,X₂,X_n是取自总体X的一个样本，对给定的数1-$a$(0<$a$<1),若存在统计量

则称随机区间(_θ,¯θ)为θ的1-$a$双侧置信区间，称1-$a$为置信度(可信度)（也称置信水平），又分别称_θ与¯θ为θ的双侧置信下限与双侧置信上限.
其中统计量可以计算出

• 性质：
  可靠度：
  要求区间以很大的可能性包含θ即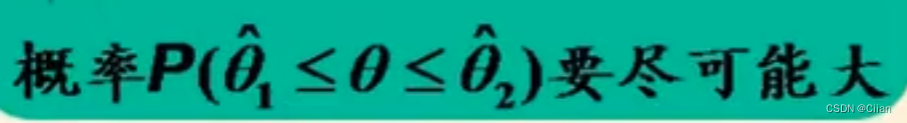
  精度：
  估计的精度要尽可能高，即区间的长度要尽可能小，或能体现此要求的其它准则。
  在保证可靠度的条件下，尽量提高精度

正态总体的置信区间

一、单正态总体均值的置信区间

1. 设总体X~N(μ,σ²),其中σ²已知，而μ为未知参数，X1,X2,Xn是取自总体X的一个样本.
   均值μ的1-a的置信区间为
   
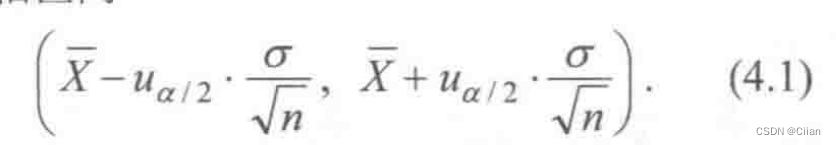
   （考）例1：
   
2. 设总体X~N(4,σ2)，其中μ，σ²未知，X1,X2,…,Xn是取自总体X的一个样本.
   此时可用σ²的无偏估计S2代替σ²，构造枢轴变量
   
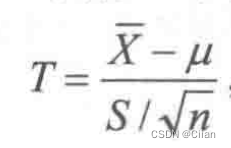
   则
   
   
   

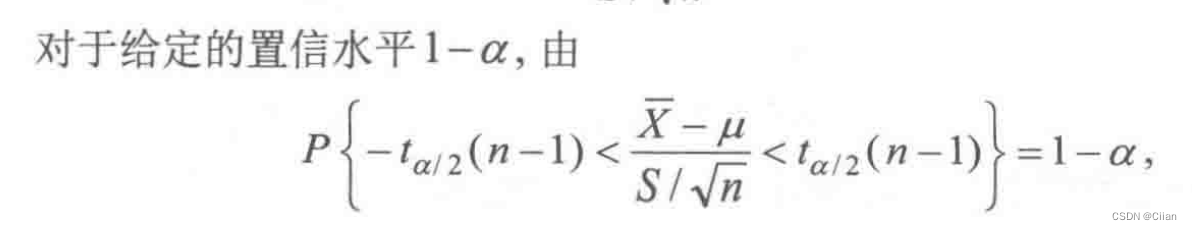
均值μ的1-a的置信区间为

三、单正态总体方差的置信区间

设总体X~N(μ,σ²),其中μ，σ²未知，X1,X2,…,Xn是取自总体X的一个样本.求方差σ²的置信度为1-a的置信区间.σ²的无偏估计为S²
有定理得

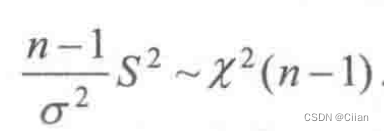
小结

单正态总体的抽样分布的三个结论