题目1：110 平衡二叉树

题目链接：110 平衡二叉树

题意

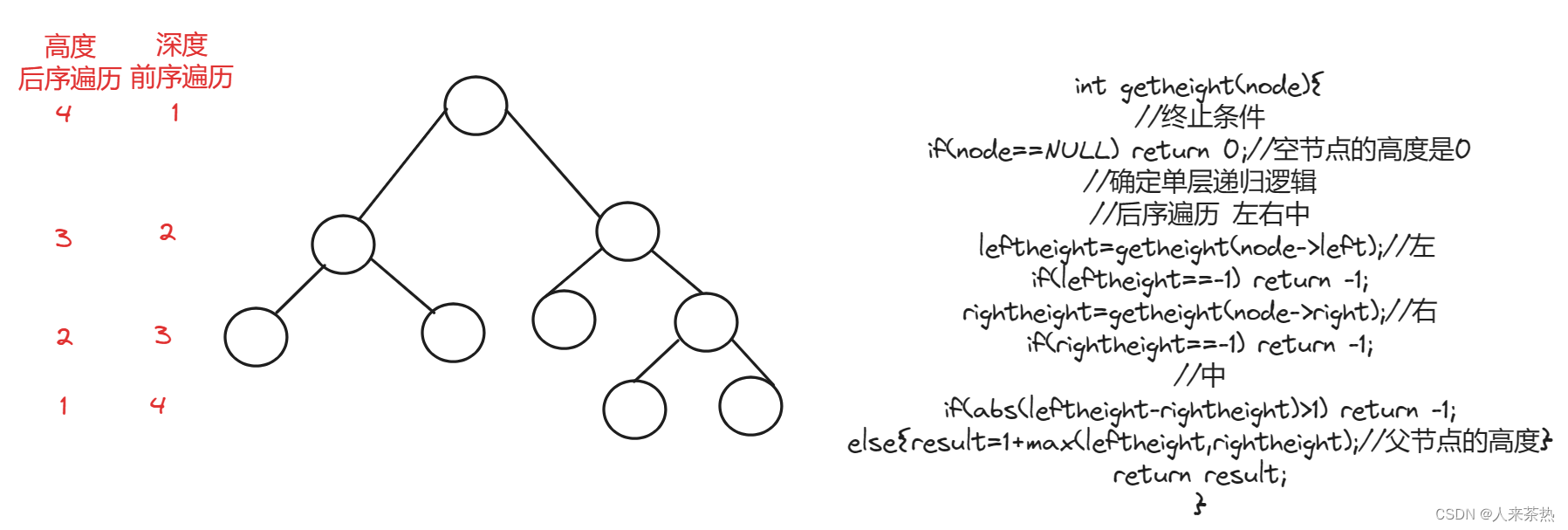
判断二叉树是否为平衡二叉树（每个节点的左右两个子树的高度差绝对值不超过1）

递归遍历

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int getheight(TreeNode* node){//终止条件if(node==NULL) return 0;int result = 0;//result一定要提前定义,是一个全局变量，最终return//单层递归逻辑 后序遍历  左右中int leftheight = getheight(node->left);//左if(leftheight==-1) return -1;int rightheight = getheight(node->right);//右if(rightheight==-1) return -1;//中if(abs(rightheight-leftheight)>1) return -1;else{result = 1 + max(leftheight,rightheight);}return result;}bool isBalanced(TreeNode* root) {int result = getheight(root);if(result==-1) return false;else return true;}
};

题目2：257 二叉树的所有路径

题目链接：257 二叉树的所有路径

题意

根据二叉树的根节点root，返回所有从根节点到叶子节点的路径（顺序任意）

递归

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* node,vector<int>& path,vector<string>& result){//中 加入后面终止条件的叶子节点path.push_back(node->val);//node->val是整型的数字//终止条件，遇到叶子节点就终止if(node->left==NULL && node->right==NULL){//将path放入到result中，注意转换类型，添加->string spath;for(int i=0;i<path.size()-1;i++){spath += to_string(path[i]);spath += "->";}spath += to_string(path[path.size()-1]);//加入最后一个，因为后面没有->，所以单独加入result.push_back(spath);return;}//单层递归逻辑  前序遍历   中左右if(node->left){traversal(node->left,path,result);//左path.pop_back();//回溯}if(node->right){traversal(node->right,path,result);//右path.pop_back();//回溯} }   vector<string> binaryTreePaths(TreeNode* root) {vector<int> path;vector<string> result;if(root==NULL) return result;traversal(root,path,result);return result;}
};

隐藏回溯

使用的是 string path，这里并没有加上引用& ，即本层递归中，path + 该节点数值，但该层递归结束，上一层path的数值并不会受到任何影响

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* node,string path,vector<string>& result){//中 加入后面终止条件的叶子节点path += to_string(node->val);//node->val是整型的数字//终止条件，遇到叶子节点就终止if(node->left==NULL && node->right==NULL){//将path放入到result中，注意转换类型，添加->result.push_back(path);return;}//单层递归逻辑  前序遍历   中左右if(node->left){traversal(node->left,path+"->",result);//左//path.pop_back();//回溯}if(node->right){traversal(node->right,path+"->",result);//右//path.pop_back();//回溯} }   vector<string> binaryTreePaths(TreeNode* root) {string path;vector<string> result;if(root==NULL) return result;traversal(root,path,result);return result;}
};

非隐藏回溯

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* node,string path,vector<string>& result){//中 加入后面终止条件的叶子节点path += to_string(node->val);//node->val是整型的数字//终止条件，遇到叶子节点就终止if(node->left==NULL && node->right==NULL){//将path放入到result中，注意转换类型，添加->result.push_back(path);return;}//单层递归逻辑  前序遍历   中左右if(node->left){path = path + "->";traversal(node->left,path,result);//左path.pop_back();//回溯 >path.pop_back();//回溯 -}if(node->right){path = path + "->";traversal(node->right,path,result);//右path.pop_back();//回溯  >path.pop_back();//回溯  -} }   vector<string> binaryTreePaths(TreeNode* root) {string path;vector<string> result;if(root==NULL) return result;traversal(root,path,result);return result;}
};

题目3：404  左叶子之和

题目链接：404 左叶子之和

题意

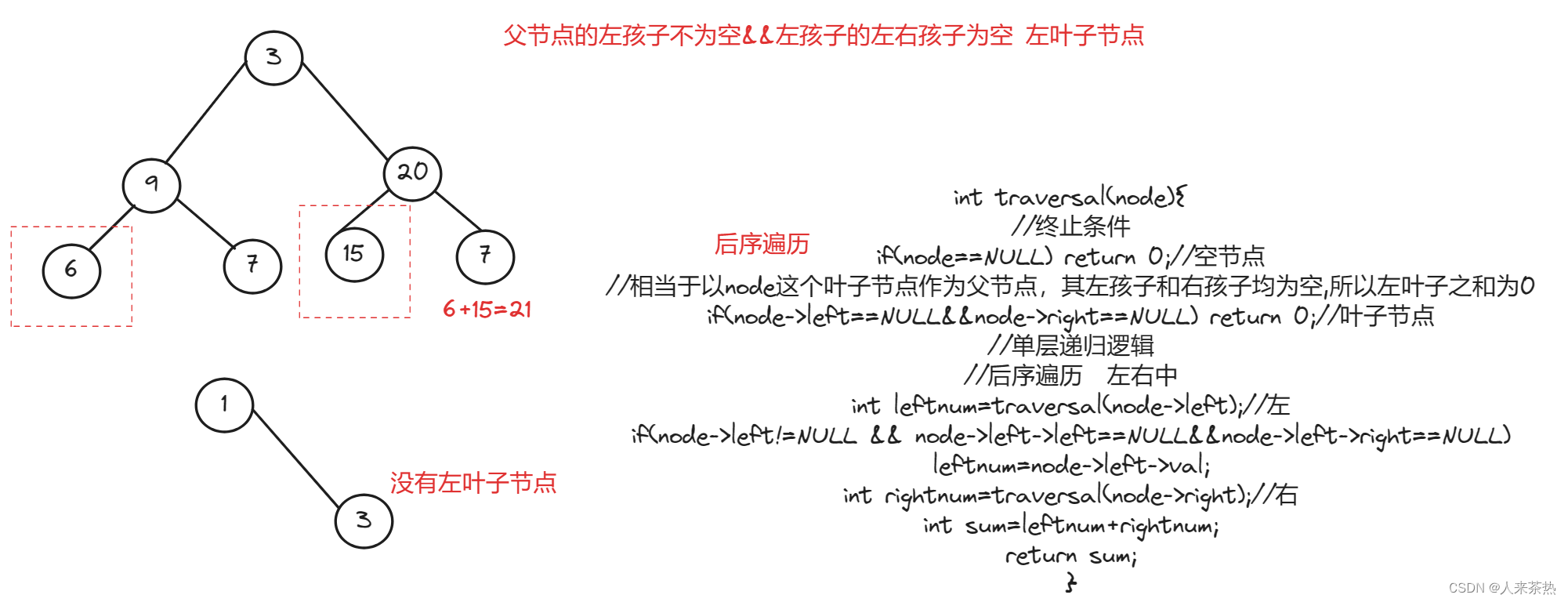
返回所有左叶子之和

一定要是叶子节点  且是父节点的左孩子，因此必须通过节点的父节点判断当前节点是否为左叶子

递归

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {//终止条件if(root==NULL) return 0;if(root->left==NULL && root->right==NULL) return 0;//单层递归逻辑  后序遍历  左右中//左int leftnum = sumOfLeftLeaves(root->left);if(root->left!=NULL && root->left->left==NULL && root->left->right==NULL) leftnum = root->left->val;//右int rightnum = sumOfLeftLeaves(root->right);//中int sum = leftnum + rightnum;return sum;}
};

迭代

因为用递归可以做的，栈也可以 

这里栈只是一个容器，换成队列也可 

前序遍历

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {stack<TreeNode*> st;if(root!=NULL) st.push(root);int sum = 0;while(!st.empty()){TreeNode* node = st.top();st.pop();if(node->left!=NULL && node->left->left==NULL && node->left->right==NULL){sum += node->left->val;}if(node->left) st.push(node->left);if(node->right) st.push(node->right);}return sum;}
};

后序遍历

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {stack<TreeNode*> st;if(root!=NULL) st.push(root);int sum = 0;while(!st.empty()){TreeNode* node = st.top();st.pop();if(node->left) st.push(node->left);if(node->right) st.push(node->right);if(node->left!=NULL && node->left->left==NULL && node->left->right==NULL){sum += node->left->val;}}return sum;}
};