Problem - D - Codeforces

题意：

用两种方式制作一个很大的数组，然后查询对应下标对应的数字。

难点：

制作的方式有复制n次原数组接到后面，样例的数据很大，很快就会溢出unsigned long long。暴力做出这个数组是不可以的。

细节：

查询的大小不会超过1e18，所以我们超过上限的不进行记录了。

方法：

我们用记录数字偏移量的方法。查找时找对应偏移量即可。->代码上我们记录操作，计算这次操作末尾的偏移量，这样查找的话可以用二分查找，很快就能找到是哪次操作的位置。

为什么要这么做：

因为是对应数字的偏移量，那么这个位置就是这个数字。

如果这个位置是复制操作，我们取余就可以得到复制前的偏移量，得到的数字也是这个数字。（如果前面还是复制操作呢？ ->其实就是子问题啦）

————

根据题目第一个样例做解释：

（pos数组是偏移量，options数组就是操作类型，val数组就是操作的值）

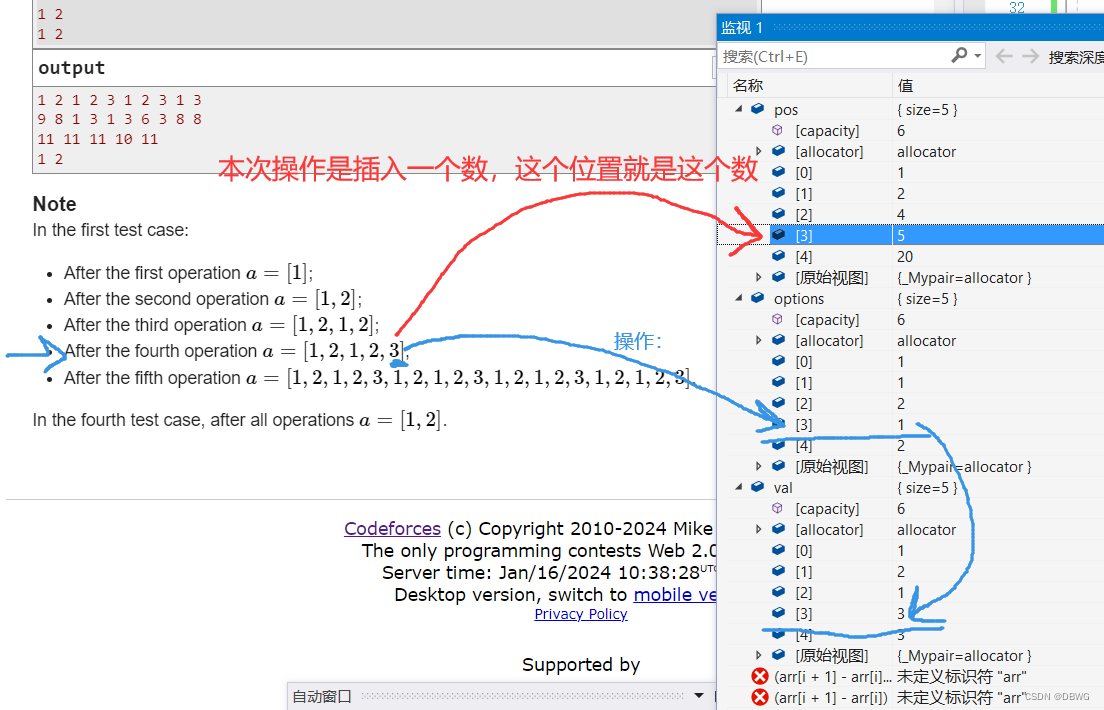
代码：注意看对超过1e18位置的处理：

#define ll unsigned long long
const ll inf = 1e18;
void solve()
{ll n, q;cin >> n >> q;vector<ll>pos;//偏移量vector<ll>val;vector<ll>options;for (ll i = 0; i < n; i++){ll op, num; cin >> op >> num;options.push_back(op);val.push_back(num);if (op == 1){if (pos.size() == 0)//第一次pos.push_back(1);else{pos.push_back(pos[i - 1] + 1);}}else{//查询不会查老后面，但是前面操作会超出if ((inf) / num < pos[i - 1]) //#### 这里是对超过1e18的处理，inf加个num向上取整更合适，不过这里也可以过pos.push_back(inf + 5);elsepos.push_back(pos[i - 1] * (num + 1));}}for (ll i = 0; i < q; i++){ll num; cin >> num;//ll left = 0, right = pos.size() - 1;while (1){while (left < right)//根据偏移量二分。二分就是找到自己在的对应操作的位置。{ll mid = left + (right - left) / 2;if (pos[mid] >= num)right = mid;else left = mid + 1;}if (options[right] == 1)//！！！偏移量正好对应的是一个数字{cout << val[right] << " ";break;}else//调整位置接着二分（num变了,划成子问题了{ll snum = pos[right - 1];//pos[right] / (val[right]+1);//这次操作的原始数组大小num %= snum;//换到对应位置if (num == 0)num = snum;left = 0;//只会在左边了，再次找}}}cout << endl;
}