正余弦优化算法(Sine cosine algorithm,SCA)是由Mirjalili [1]在2016年提出,目前WOS上引用量2K+,谷歌学术上4K+。

不得不说Seyedali Mirjalili真是位大神级的人物(下图是Mirjalili开发的部分算法)
SCA的核心思想是利用正、余弦函数波动的周期性,在全局范围内探索最优解,使算法逐步收敛。其具有结构简单、参数少、易于实现的特点。其优化性能优于GA、PSO、花授粉等,已被广泛用于数据分类、光谱特征峰定位和电力系统调度等不同领域。
另一方面,算法的混合来看,混合元启发式算法的主要目标是利用每种算法的优点,以最大限度地减少每种算法的缺点。正是由于SCA模型的简单及其优秀的搜索性能,其更易于算法的混合。
本文主要内容包括:SCA算法原理,SCA算法的改进与利用思路,以及SCA算法的MATLAB和Python代码实现。
00 目录
1 正余弦算法SCA原理
2 改进&利用
3 代码目录
4 算法性能
5 源码获取
01 正余弦算法SCA原理
SCA的独特之处在于使用正弦和余弦波来控制探索和开发搜索空间。下面的数学方程可以描述这个过程:
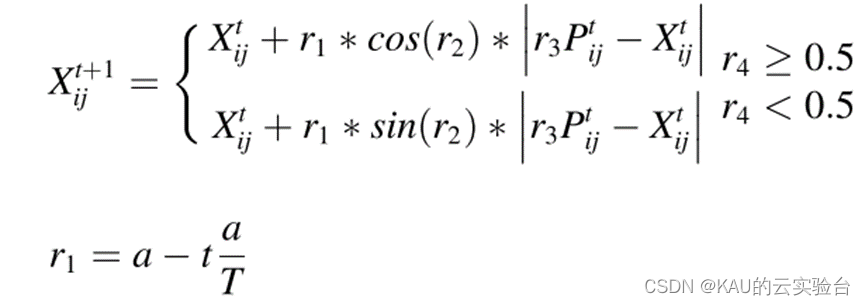
Pt ij指示迭代t中的最佳个体位置。此外,有四个随机参数r1,r2,r3和r4。r1控制搜索代理的下一个位置,如果r1小于1,则倾向于开发,如果r1大于1,则倾向于勘探。为了平衡勘探与开发,r1的定义式是线性递减的,其中a一般取2。r2表示向外或向内的移动步长,r2参数的范围是[0,2 π]。r3在0和2之间的范围内,如果r3大于1,则更注重全局最优位置,否则不强调。r4是在0和1之间的随机参数,用以转换正弦和余弦。
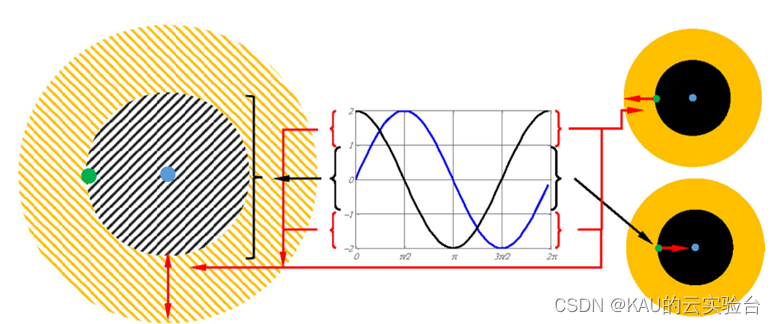
其寻优示意图如下:
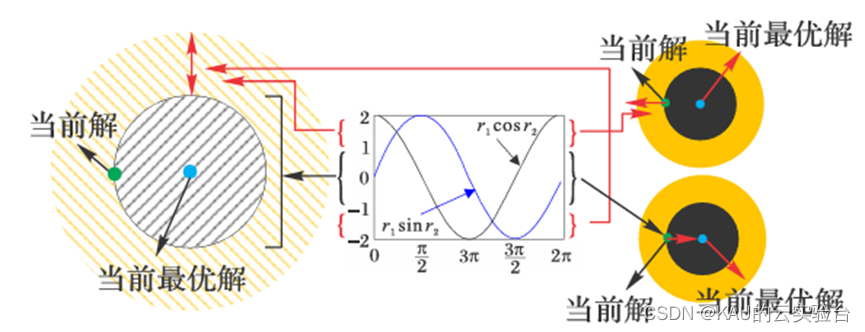
图:陈亮, 汤显峰. 改进正余弦算法优化特征选择及数据分类[J]. 计算机应用, 2022, 42(6): 1852-1861.
以上就是SCA的全部理论,很简单吧~
02 改进&利用
根据没有免费的午餐(NFL)定理[2],没有一个算法可以处理所有的优化问题,即每个算法都有其优势和局限性,这也激励着学者提出各种改进的算法来解决不同类型的优化问题,同时也为算法间的混合利用提供了参考。
2.1 改进
SCA在面对复杂问题时仍然存在优化精度低、容易陷入局部极值、收敛速度慢等问题,这里给出一种思路。SCA中,r1用于平衡全局搜索和局部开发能力,但线性递减的策略使得前期递减的过快,全局搜索不充分,后期递减的过慢,无法快速收敛,因此可以设计一种非线性的参数r1以提高其搜索能力。同时,针对其易陷入局部最优的问题,也可以引入如Levy等变异策略。
2.2 利用
SCA模型的正余弦震荡变化特性使其在解空间具有良好的搜索能力,可以直接引入该式替换算法某部分的寻优,或是将其融入算法的更新方程中,如下是一篇文献[A collaboration-based hybrid GWO-SCA optimizer for engineering optimization problems]的思路(将SCA融入GWO中):
原GWO算法
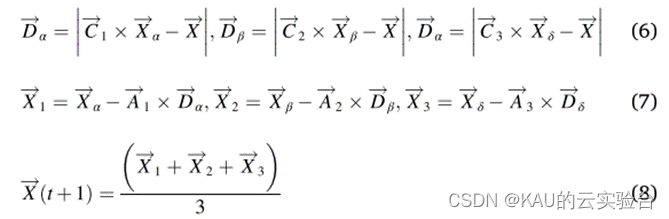
融入SCA的GWO算法
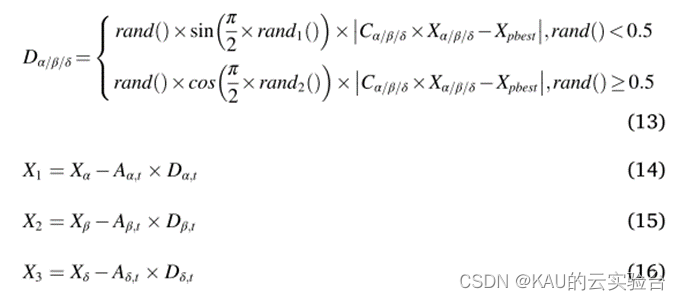
03 代码目录
代码包含MATLAB和Python,考虑到很多同学获取代码后,MATLAB代码部分有乱码(MATLAB版本问题),可以将MATLAB版本改为2020及以上,或使用乱码解决文件夹中的txt文件即可。
代码都经过作者重新注释,代码更清爽,可读性强。
部分代码:(MATLAB与Python)
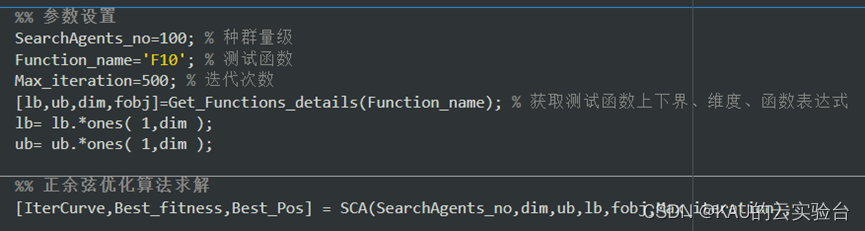
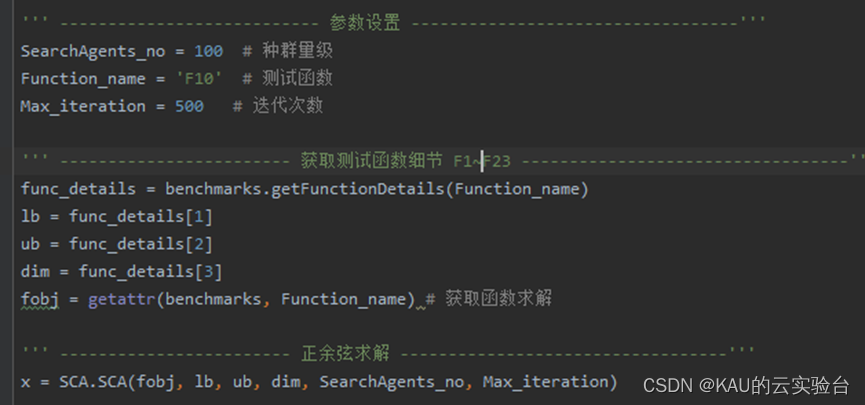
04算法性能
采用标准测试函数初步检验其寻优性能
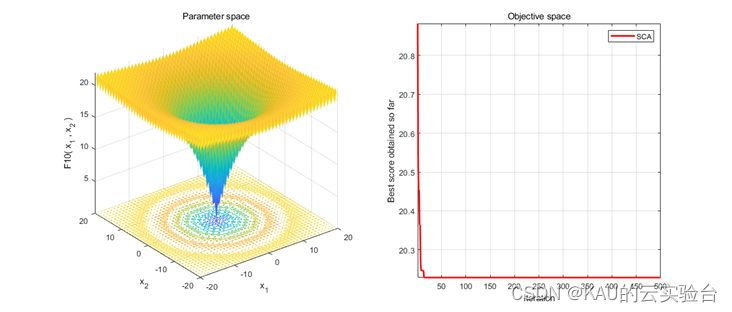
在Matlab中,进行CEC2005函数的测试,执行程序结果如下:
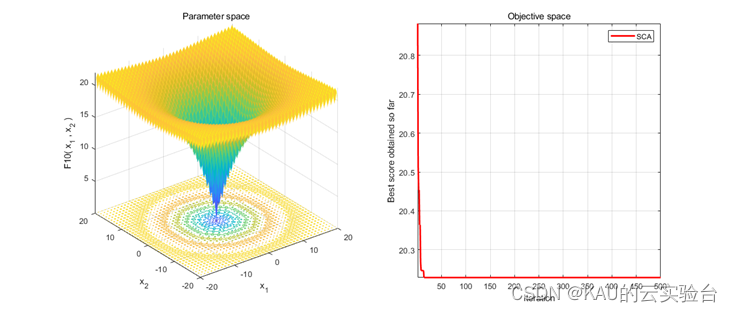
在Python中,进行CEC2005函数的测试,执行程序结果如下:
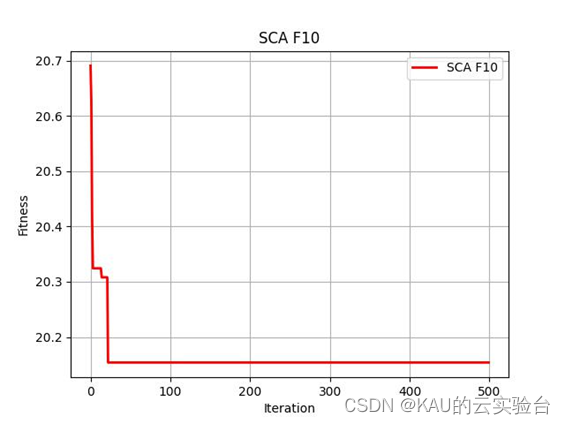
05 源码获取
在GZH(KAU的云实验台)后台回复 SCA 即可
参考文献
[1] MIRJALILI S.SCA:A sine cosine algorithm for solving optimization problems[J].Knowledge-Based Systems,2016,96:120-133.
[2] Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE transactions on evolutionary computation 67–82, 1997.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!