流媒体播放器EasyPlayer是TSINGSEE青犀流媒体组件系列中关注度较高的产品，经过多年的发展和迭代，目前已经有多个应用版本，包括RTSP版、RTMP版、Pro版，以及js版，其中js版本作为网页播放器，受到了用户的广泛使用。在功能上，EasyPlayer支持直播、点播、录像、快照截图、MP4播放、多屏播放、倍数播放、全屏播放等特性，具备较高的可用性和稳定性。为了便于用户集成与调用，我们也提供了API接口供大家使用。

有用户反馈，集成EasyPlayer.js后，在自己本地环境下出现了网络波动恢复后不能重新拉流播放的情况，请求我们协助排查。

排查思路：

1）出现这种情况，首先检查视频流播放是否正常，如果视频流播放正常，那就需要查看播放器了。

2）后续排查发现，用户在集成EasyPlayer.js播放器时，没有配置重连属性；

3）只需要在项目本地配置重连属性，就可以在网络恢复后重连播放了。

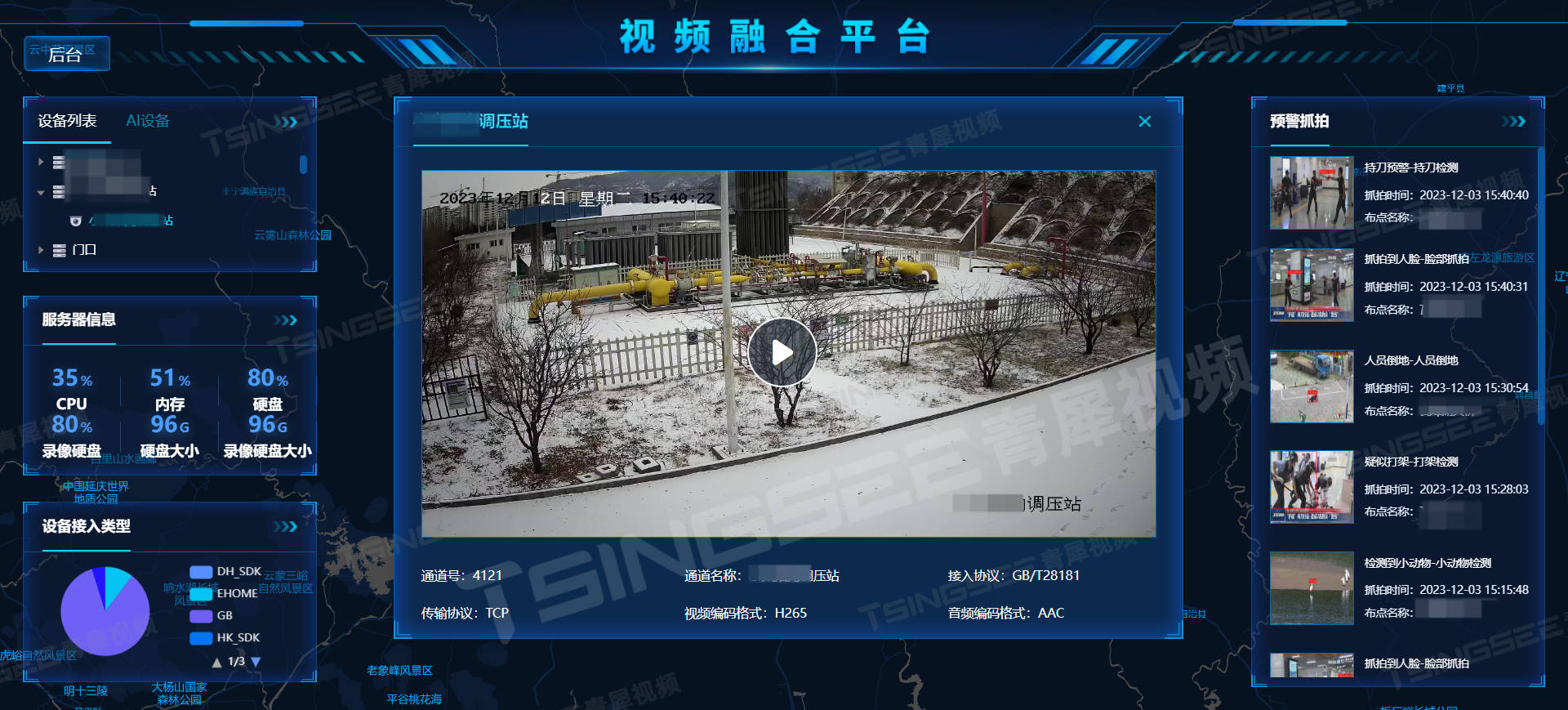
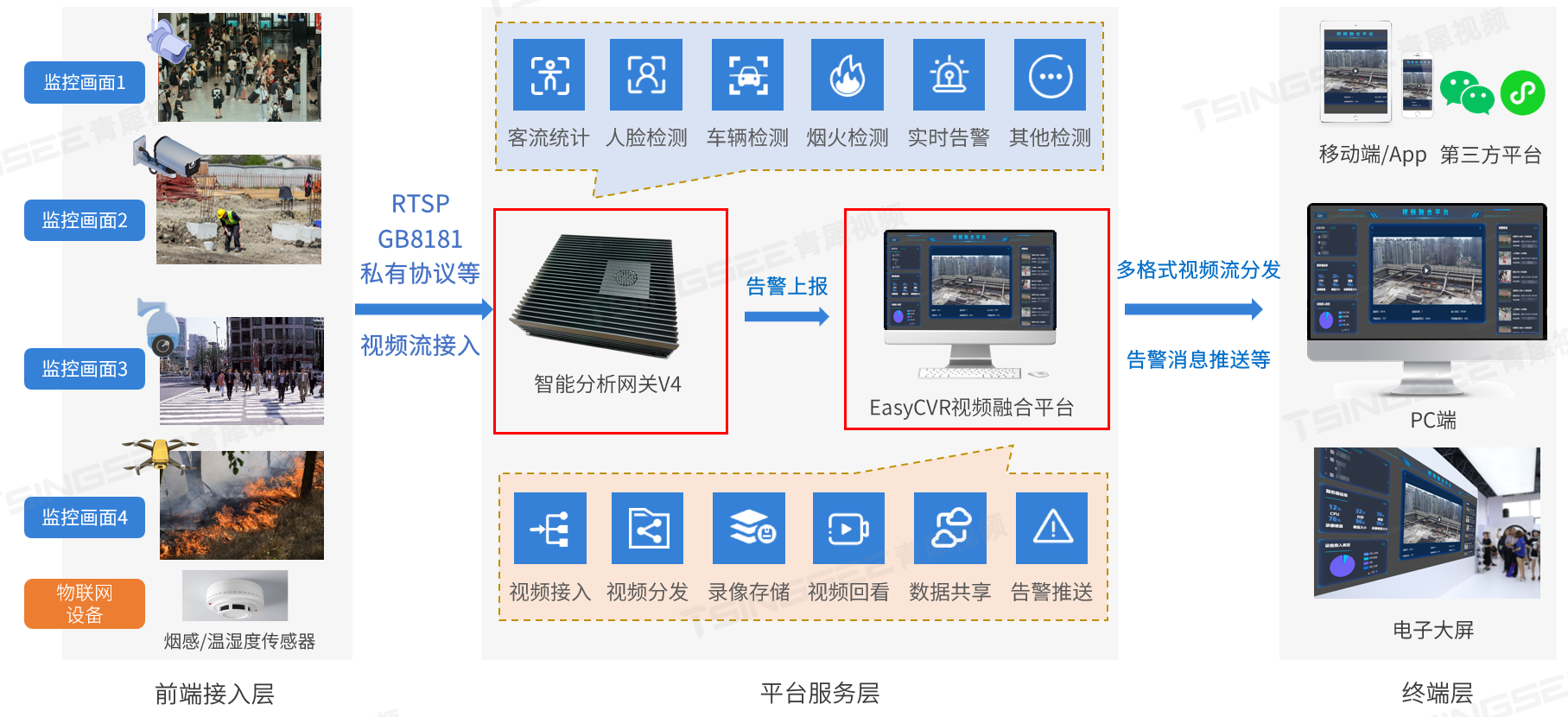
H5无插件流媒体播放器EasyPlayer可支持H.264与H.265编码格式，性能稳定、播放流畅，能支持WebSocket-FLV、HTTP-FLV，HLS（m3u8）、WebRTC等格式的视频流。EasyPlayer播放器系列依赖其灵活控制、低延时、高稳定的特点，已经成熟运用于多个项目场景当中，其中包括手机直播、电脑桌面直播等。感兴趣的用户可以自行下载测试。