绘制数据流图(L0/L1/L2)

DFD/L0（基本系统模型）

只包含源点终点和一个处理(XXX系统)

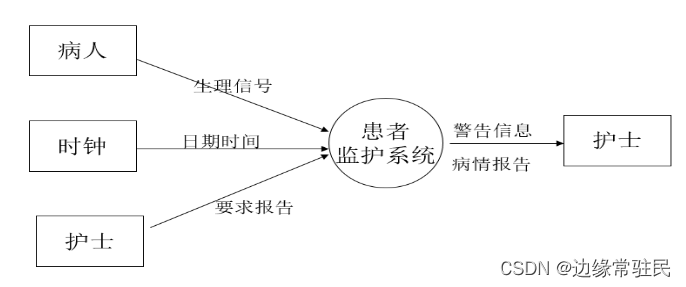
DFD/L1（功能级数据流图）在L0基础上进一步划分处理(XXX系统)

个人理解

 

DFD/L2（在L1基础上进一步分解后的数据流图）

数据流图转软件结构图

变换流

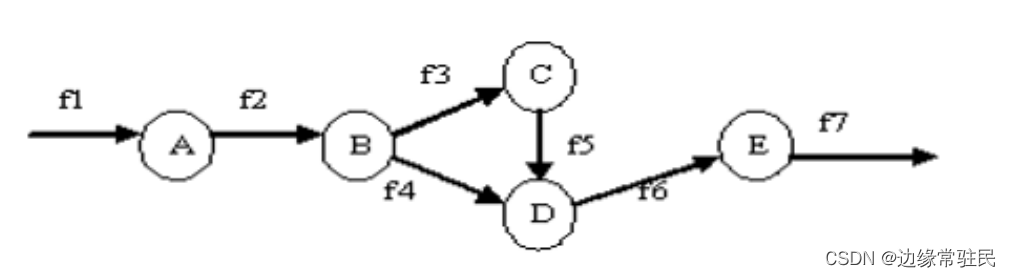
以CD为变换中心         

箭头尾部记得加圆圈(空心圆代表传递的数据，实心圆代表传递的控制信息)，一般都是传递数据

以D为变换中心

 

事务流

绘制状态转换图

授课老师亲笔展示 

绘制流图(退化的程序流程图)计算环路复杂度、确立独立路径、设计测试用例

第六章例子

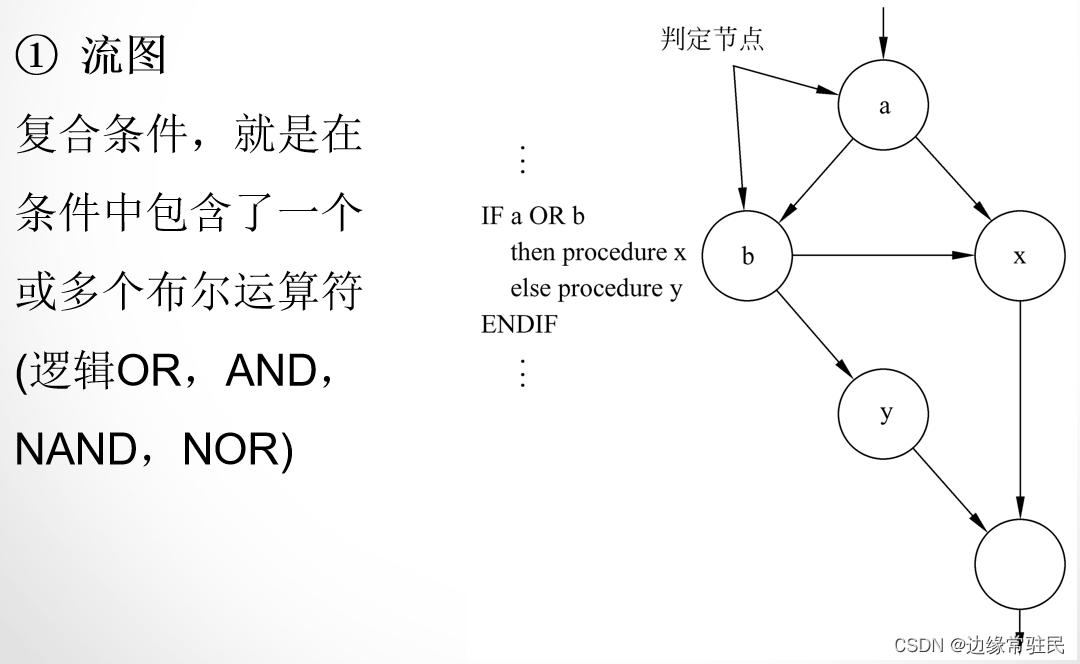
该流图的环形复杂度为3

a的上边应该有一个开始节点        最下边也应该还有一个结束节点

一共是8条边，7个节点        环形复杂度 = 8 - 7 + 2 = 3 = 判定节点数 + 1

计算环形复杂度的方法

(1) 流图中线性无关的区域数等于环形复杂度

(2) 流图G的环形复杂度V(G)=E-N+2,其中，E是流图中边的条数，N是结点数

(3) 流图G的环形复杂度V(G)=P+1，其中，P是流图中判定结点的数目

第七章基本路径测试

基本路径测试是Tom McCabe提出的一种白盒测试技术。使用基本路径测试设计测试用例时，首先计算程序的环形复杂度，并用该复杂度为指南定义执行路径的基本集合，从该基本集合导出的测试用例可以保证程序中的每条语句至少执行一次，而且每个条件在执行时都将分别取真、假两种值

1.根据过程设计结果画出相应的流图

2.计算流图的环形复杂度

        1.上图中共有5个判定节点(含分叉的节点2，3，5，6，10) 5 + 1 = 6

        2.边数17 - 结点数13 + 2 = 6

3.确定线性独立路径的基本集合

独立路径是指至少引入程序的一个新处理语句集合或一个新条件的路径，即独立路径至少包含一条在定义该路径之前不曾用过的边

程序的环形复杂度决定了程序中独立路径的数量，而且这个数是确保程序中所有语句至少被执行一次所需的测试数量的上界

上述程序的环形复杂度为6，因此共有6条独立路径 

路径1： 1-2-10-11-13        路径2： 1-2-10-12-13     路径3： 1-2-3-10-11(12)-13      

路径4： 1-2-3-4-5-8-9-2-…     路径5： 1-2-3-4-5-6-8-9-2-…     路径6： 1-2-3-4-5-6-7-8-9-2-…

4.设计可强制执行基本集合中每条路径的测试用例

具体结合路径各节点的判定条件设计测试用例

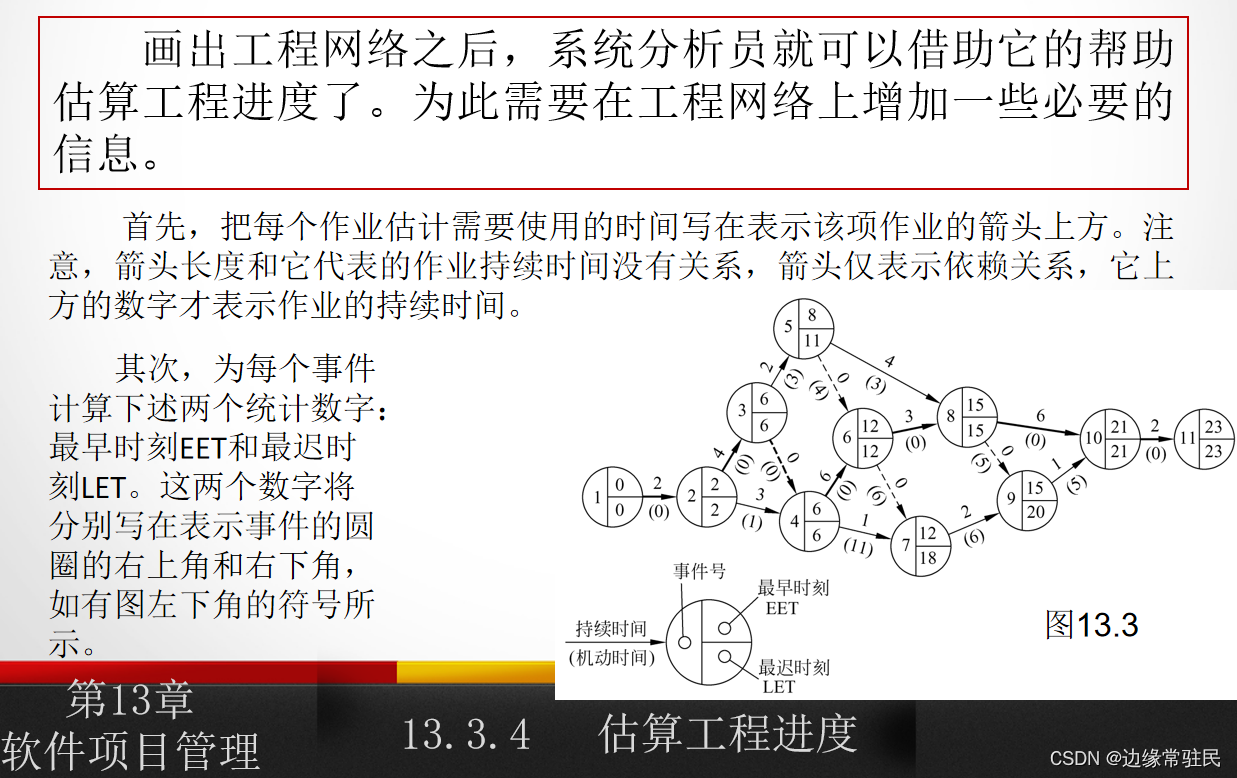
根据工程网络计算最早时刻、最迟时刻、关键路径、关键活动、机动时间