视频： https://www.bilibili.com/video/BV1KA411N7Px/?spm_id_from=autoNext&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
课件： https://zh-v2.d2l.ai/chapter_preliminaries/autograd.html
课上PPT： https://courses.d2l.ai/zh-v2/assets/pdfs/part-0_7.pdf
从入门到放弃说的就是这两节课~~~

1. 自动求导

自动求导是怎么做出来的–计算图–等价于链式法则求导的过程

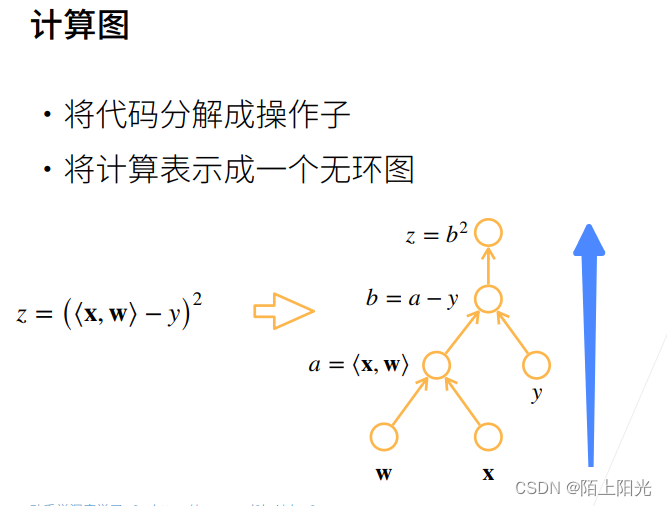
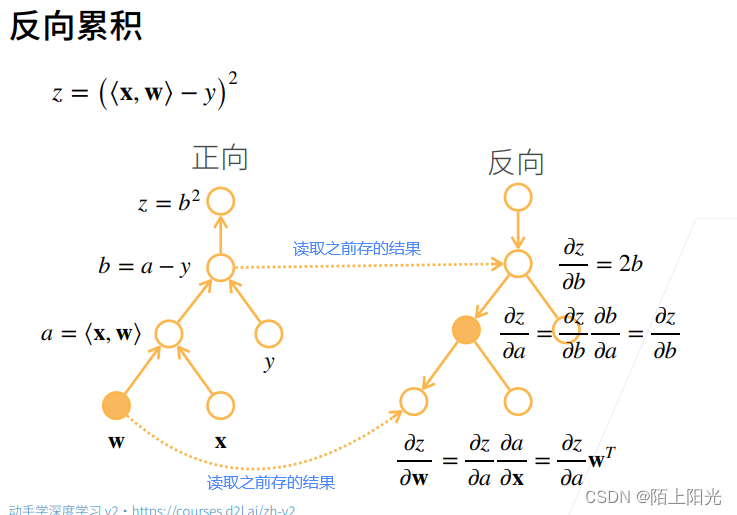
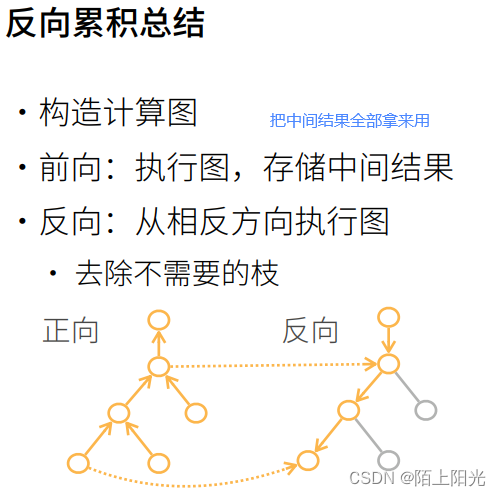
反向传播，内存复杂度O(n)，存储正向计算的所有中间结果，也是深度神经网络非常耗gpu资源的原因。

正向累积需要对每一层计算梯度，计算复杂度太高【每一层应该也有很多变量】

2. 自动求导实现

1. 示例 $y=2X^{T}X$ 关于列向量x求导。

y=sum(x) , 导数是全为1的向量

import torchx = torch.arange(4.0)
print(x)
# 设置一个地方 保存梯度 不会在每次对一个参数求导时都分配新的内存
# 一个标量函数关于向量x的梯度是向量，并且与x具有相同的形状
# x = torch.arange(4.0, requires_grad=True)  # 定义后再调梯度或者定义向量的时候就指定requires_grad参数，效果是一样的
x.requires_grad_(True)
print(x.grad)  # 访问梯度--等价于y关于x的导数存放在这里 默认值是None 
# 计算y 标量
y = 2 * torch.dot(x, x)
print(y) # torch会记住所有操作 grad_fn=<MulBackward0> 隐式构建计算图，有求梯度的函数grad_fn存放在这里 告知系统y是从x计算过来的
# 调用反向传播函数 计算y关于x每个分量的梯度 梯度与x同形状
y.backward()  # 求导
print(x.grad) # 访问梯度--导数
# 函数y=2x^Tx 关于x的梯度应为4x
print(x.grad == 4*x)
# 计算x的另一个函数，此时可以认为是另一层网络了，上一层的计算已经结束 梯度的值需要清零
# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_() # pytorch下划线表示重新写入内容 zero-置零
y = x.sum() # 求向量的sum函数 梯度等于全1
y.backward()
print(x.grad) # 在梯度不清零的情况下直接求导，梯度会在原来的值上做累加求和 [0.,4.,8.,12.]+[1.,1.,1.,1.]=[1.,5.,9.,13.]

tensor([0., 1., 2., 3.])
None
tensor(28., grad_fn=<MulBackward0>) 
tensor([ 0.,  4.,  8., 12.])
tensor([True, True, True, True])
tensor([ 1.,  5.,  9., 13.])

2. 非标量变量的反向传播

假设y也是一个向量，向量对向量的求导是一个矩阵。深度学习中很少对向量求导，一般是对标量求导。对y向量做求和–是标量后再求导。

x.grad.zero_()
y = x * x
y.sum().backward()
print(x.grad)
x.grad == 2 * x

tensor([0., 2., 4., 6.])
tensor([True, True, True, True])

在什么情况下需要对y做求和呢？

3. 分离计算

在某层网络需要把参数固定的时候，会用到这个功能
在PyTorch中，y.detach()是一个用于从计算图中分离张量的方法。计算图是PyTorch用于自动微分的关键概念，用于构建和跟踪张量之间的操作。在计算图中，张量的计算历史被记录下来，以便在反向传播时计算梯度。但有时我们希望从计算图中分离出某个张量，使其不再与原始的计算历史关联。这在某些情况下是很有用的，例如当我们只关心使用该张量进行正向传播的结果，并且不需要计算梯度时。
当调用y.detach()时，将返回一个与y相同数据但不再与计算图关联的新张量。这意味着对返回的张量进行操作不会对原始计算图产生任何影响，也不会计算任何梯度。该方法可用于将张量作为输入传递给不允许梯度传播的函数或模型。

x.grad.zero_()
y = x * x
u = y.detach()  # 把y看成一个常数赋给u u与x无关，是一个常数
print(u)
z = u * x  # z对x的导数 
z.sum().backward()
print(x.grad)
print(u == x.grad)# u是常数不是x的函数，y还是x的函数，还是可以对y求x的导数
x.grad.zero_()
y.sum().backward()
print(x.grad)
print(x.grad == 2*x)

tensor([0., 1., 4., 9.])
tensor([0., 1., 4., 9.])
tensor([True, True, True, True])
tensor([0., 2., 4., 6.])
tensor([True, True, True, True])

4. Python控制流的梯度计算

当用一个很复杂的python控制流的时候，依然可以求导。
不论中间的控制流怎么复杂，可以看成一个整体，认为d=f(a)=k*a， 导数为k，
k=d/a

def f(a):b = a * 2while b.norm() < 1000:b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn ca = torch.randn(size=(), requires_grad=True) # torch.randn()是一个用于生成服从标准正态分布（均值为0，标准差为1）的随机数的函数
d = f(a)
d.backward()
print(a)
print(d)
print(a.grad)
print(d/a)
print(a.grad == d/a) # 为什么这两个值相等 不论中间的控制流怎么复杂，可以看成一个整体，认为d=f(a)=k*a， 导数为k，k=d/a

tensor(0.5429, requires_grad=True)
tensor(1111.8456, grad_fn=<MulBackward0>)
tensor(2048.)
tensor(2048., grad_fn=<DivBackward0>)
tensor(True)

pytorch隐式构造的好处，控制流的使用更好一些，但是慢一些。

QA

1. ppt上隐式构造和显示构造为什么看起来差不多？

主要区别：显示构造：先写出整个计算，再去给值
数学和python代码实现上很不一样，实际使用，正向显示构造很不方便

2. 需要正向反向都算一遍吗

神经网络求梯度： 正着算一遍【算出函数y的值】，反着算一遍【自动求导】

3. 为什么pytorch会默认累积梯度

设计理念。通常有大批量时候，算一次算不出来梯度，就把大批量分成小批量，然后就需要累积梯度。
weight在不同模型使用的时候，累加是有好处的。

4. 为什么是0246， x^2对x求导这样理解吗？

x * x 导数是2x， 【0,1，2,3】*2=【0,2，4,6】

5. 为什么深度学习中一般对标量求导而不是对矩阵或者向量

因为loss【精度等】通常是一个标量，如果loss是向量，向量关于矩阵的loss是矩阵，神经网络展开会变成很高维的张量，无法计算。

6.多个loss函数分别反向的时候是需要累加梯度的

为什么pytorch默认累加梯度的原因

7. 为什么获取.grad前需要backward

计算梯度是一个很贵的事情，会占用很多资源，不调用backward是不会自动计算梯度的，需要手动调用。

8. 求导的过程一般来说是不是都是有向图，可以用树状结构来表示，有其他环状的图结构吗

循环神经网络可以变成环状结构【逻辑上】，但是计算上还是展开的，在图上表示是展开的，做梯度累加

9. pytorch或mxnet框架可以实现矢量的求导

支持高阶求导，在二阶优化算法可以实现，但是速度很慢。