归并排序详解

基本思想：

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先试每个子序列有序，再使子序列段间7有序。若将两个有序表合并成一个有序表，成为二路归并。归并排序核心步骤：
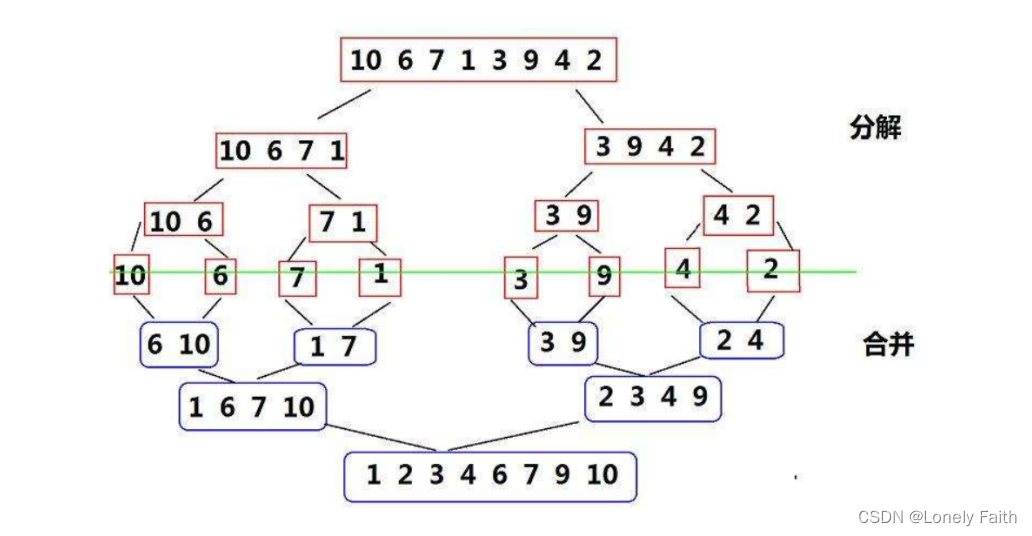
归并示意图
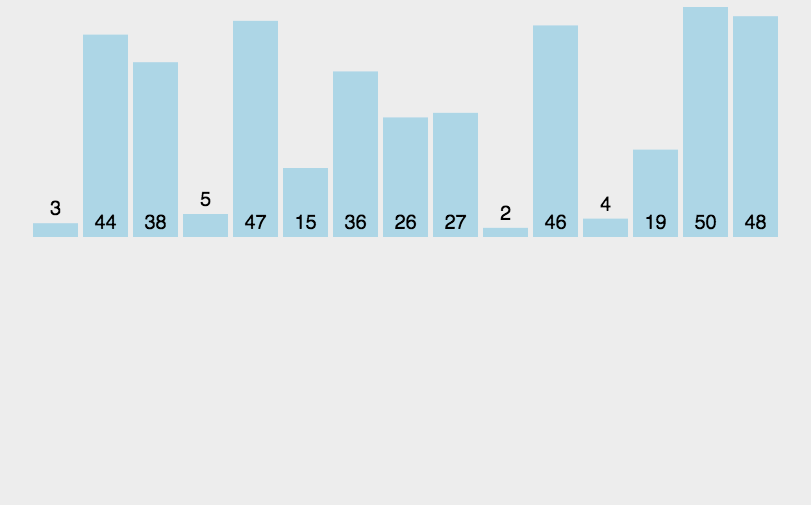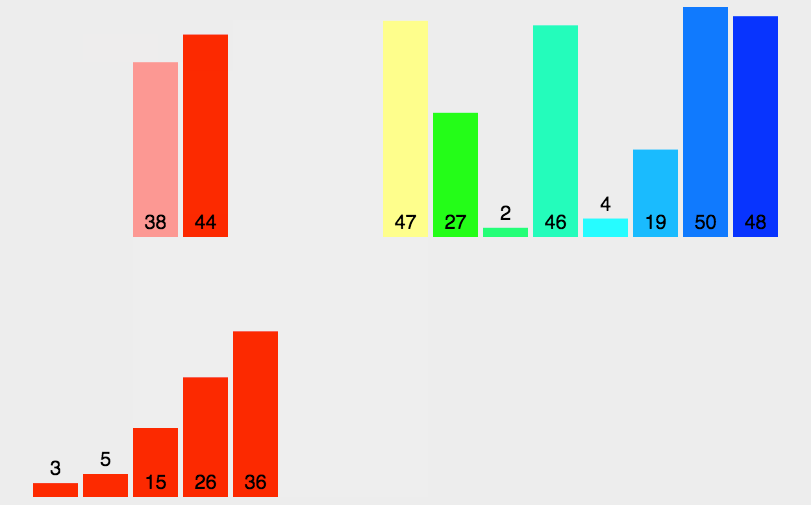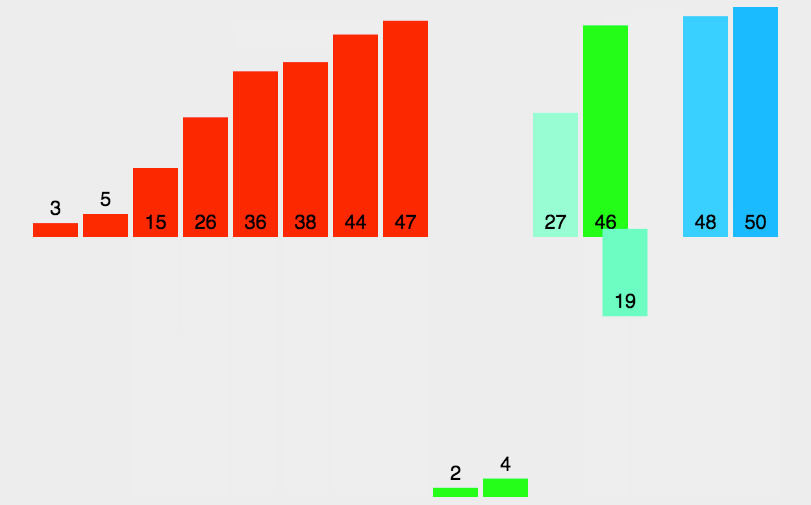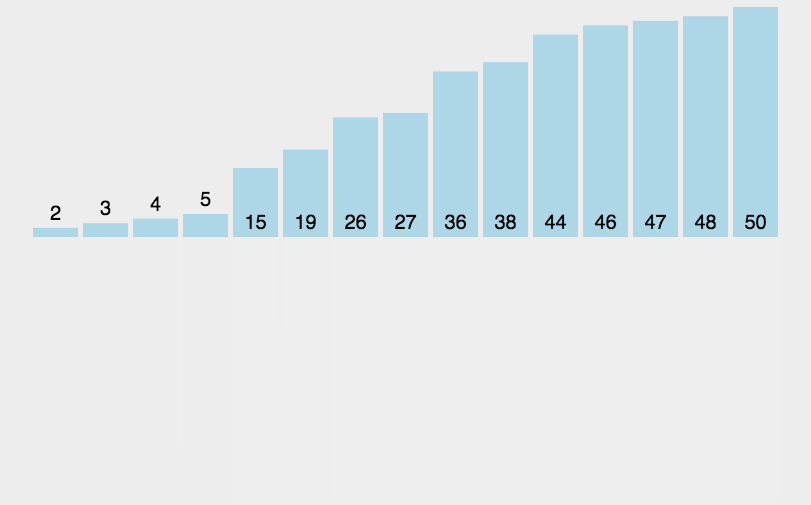
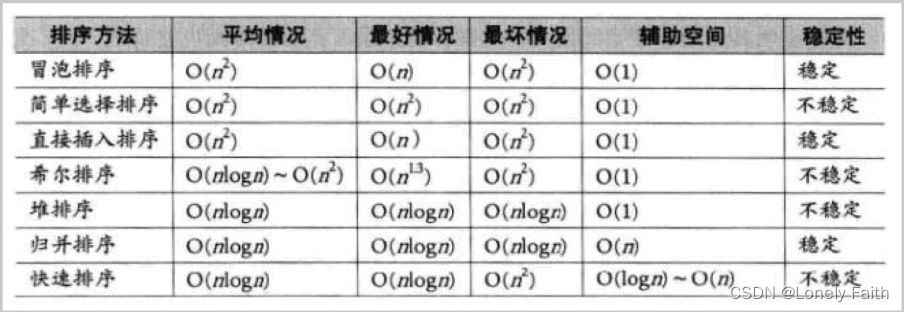
在这里插入图片描述

归并排序的特性总结：

归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
时间复杂度：O(N*logN)
空间复杂度：O(N)
稳定性：稳定
代码（递归版本）：

void _MergeSort(int* a,int begin, int end, int* tmp)
{if (begin == end){return;}if ((end - begin + 1) < 10 ){InsertSort(a+begin, end - begin + 1);return;}int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}//时间复杂度O(logN * N)
//空间复杂度O(N)
void MergeSort(int* a, int n)
{int* tmp = malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}