文章目录
- 失真
- 失真的一种现象-码间串扰
- 奈氏准则(奈溃斯特定理)
- 例题
- 香农定理
- 例题
- 奈氏和香农
失真
就是指与原来的不一样了
两种情况
前三个是正相关,最后一个是负相关
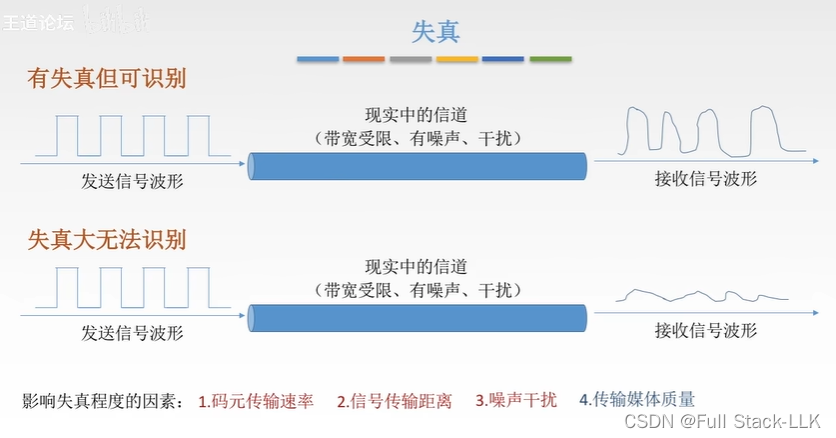
码元传输速率越快,失真程度越严重的原因可能包括以下几点:
- 信号的频率成分增加:随着码元传输速率的提高,信号的频率成分也会相应增加。高频信号更容易受到电路特性的影响,如电阻、电容和电感等元件的响应特性,这可能导致信号波形发生变化,从而产生失真。
- 信道带宽限制:根据奈氏准则,为了避免码间串扰,码元的传输速率有一个上限值,即信道的最大带宽。如果传输速率超过这个极限,就会导致信号之间的相互干扰,进而产生失真。
- 信号衰减和噪声干扰:随着传输速率的提高,信号在传输介质中的衰减也会加剧,同时噪声对信号的影响也会变得更为显著。这些因素都可能导致接收端的信号质量下降,从而增加了失真的风险。
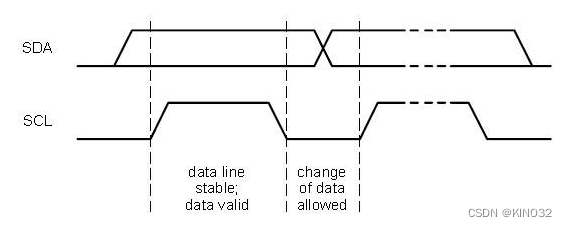
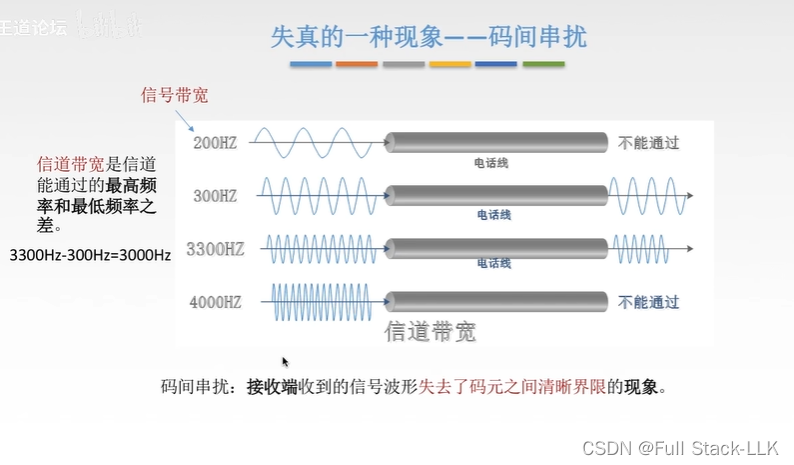
失真的一种现象-码间串扰
模拟信号是连续的,电话信道是模拟信道
模拟信号的信号带宽是频率
信号带宽不等于信道带宽
200HZ不能通过的原因是容易收到其他高频率信号的影响,导致其衰减很大或收到干扰很大甚至以至于消失了,所以说不能通过
4000HZ不能通过的原因是因为其振动频率太快了,导致其时间间隔太短了都分不清码元之间的界限了或者说码元传输速率太快导致其分不清码元之间的界限了又或者说码元长度太短了,经过时被识别的时间太短了,来不及分辨处理好
就像一群人连续过来,你能否分辨每一个人。和一个人一个人走过来,你能否分辨好每一个人那种效果
传输速率慢
高低都是码元信号
 传输速率快
传输速率快

频率高=信号变化快=码元变化快=码元传输速率快(更密集,码元长度更短,速度更快)
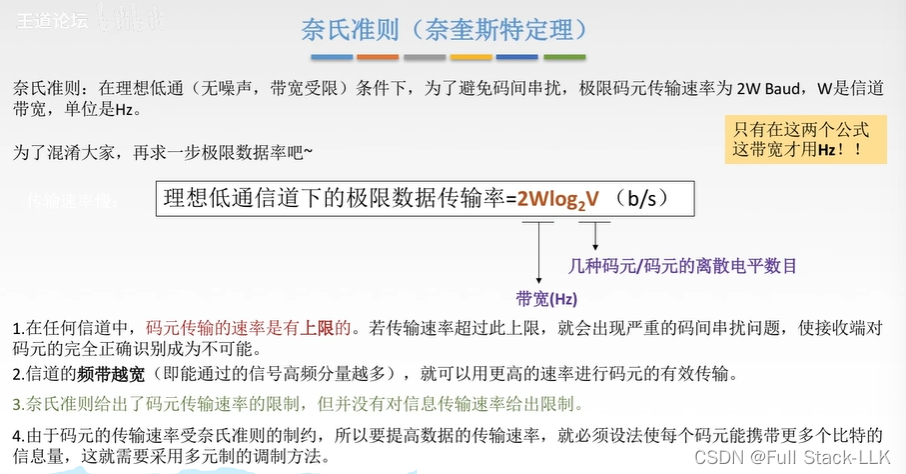
奈氏准则(奈溃斯特定理)
理想(无外界干扰)低通(带宽受限,低于最高频率可以通过)
用来限制码元传输速率
频带越宽=信道带宽越大
例题
每个相位4种振幅,总共16种振幅,那么十六种波形信号,

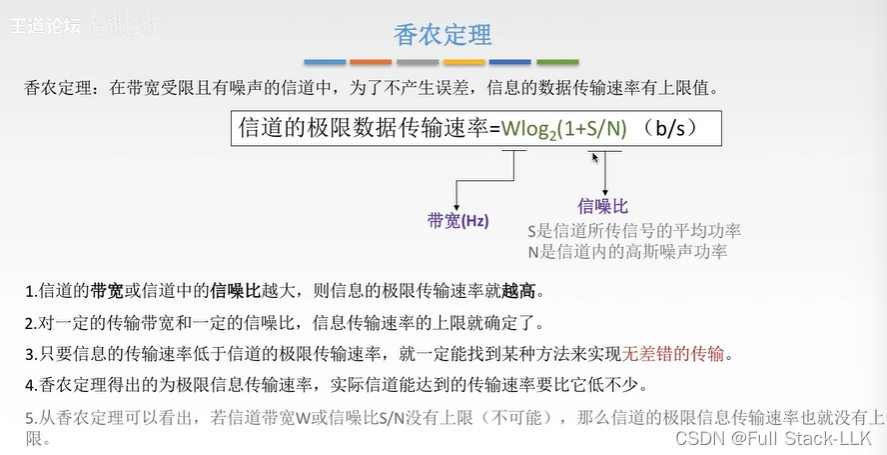
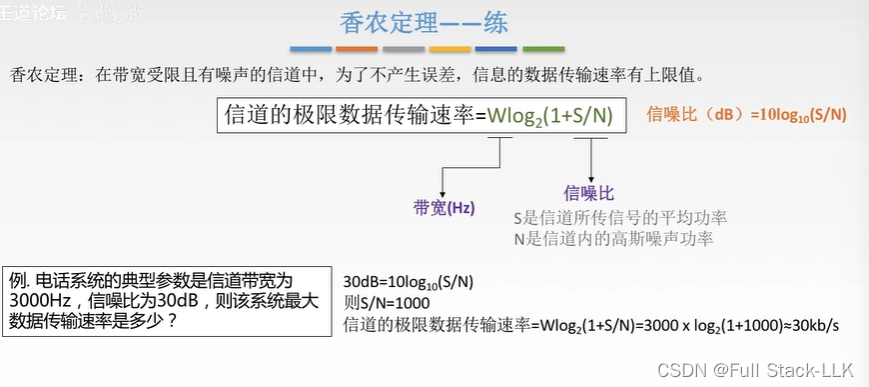
香农定理
信噪可类比学生接收老师声音和学渣声音
不产生误差指的是接收端能得到正确的信号

无差错的传输就是说没有误差
例题
奈氏和香农
奈氏:减少内部码元之间的信号
香农:在噪声影响下的限制,是外在的
二者都可以求的时候分别求然后取更小的,此时更小的能够保证此时两种都能满足

![[MQ]常用的mq产品图形管理web界面或客户端](https://img-blog.csdnimg.cn/direct/de1cd254ef1144d9ade10d2dc3a454e7.png)