Leetcode204. 计数质数
题目
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
代码
class Solution:def countPrimes(self, n: int) -> int:if n < 2:return 0prime_arr = [1 for _ in range(n)]prime_arr[0], prime_arr[1] = 0, 0ls = list()for i in range(2, n):if prime_arr[i]:ls.append(i)length = len(ls)for j in range(length):if i * ls[j] > n:breakprime_arr[i * ls] = 0return sum(prime_arr)
Leetcode858. 镜面反射
题目
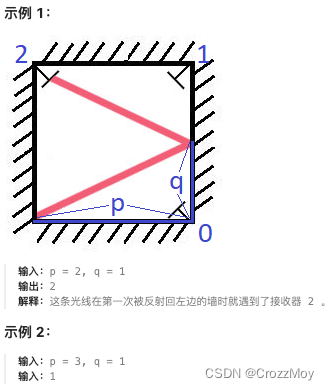
有一个特殊的正方形房间,每面墙上都有一面镜子。除西南角以外,每个角落都放有一个接受器,编号为 0, 1,以及 2。
正方形房间的墙壁长度为 p,一束激光从西南角射出,首先会与东墙相遇,入射点到接收器 0 的距离为 q 。
返回光线最先遇到的接收器的编号(保证光线最终会遇到一个接收器)。
代码
class Solution:def mirrorReflection(self, p: int, q: int) -> int:# 两个都是偶数要约分while not p & 1 and not q & 1:p >>= 1q >>= 1# p为偶数if not p & 1:return 2# p为奇数,q为偶数if not q & 1:return 0# p为奇数,q为奇数return 1
Leetcode952. 按公因数计算最大组件大小
题目
给定一个由不同正整数的组成的非空数组 nums ,考虑下面的图:
- 有 nums.length 个节点,按从 nums[0] 到 nums[nums.length - 1] 标记;
- 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时,nums[i] 和 nums[j]之间才有一条边。
返回 图中最大连通组件的大小 。
代码
class Solution:def largestComponentSize(self, nums: List[int]) -> int:n = max(nums) + 1# 欧拉筛prime_arr = [1 for _ in range(n)]prime_arr[0], prime_arr[1] = 0, 0ls = []for i in range(2, int(math.sqrt(n) + 1)):if prime_arr[i]:ls.append(i)length = len(ls)for j in range(length):if i * ls[j] > n - 1:breakprime_arr[i * ls[j]] = 0if i % ls[j] == 0:break# 初始化并查集parent = [i for i in range(n)]def find(x):if parent[x] != x:parent[x] = find(parent[x])return parent[x]def union(a, b):parent_a, parent_b = find(a), find(b)if parent_a != parent_b:parent[parent_a] = parent_bfor i, num in enumerate(nums):quotient = numk = len(ls)# 遍历所有质数并且这些质数的平方和不能大于当前numfor j in range(k):if ls[j] * ls[j] <= quotient and not quotient % ls[j]:union(num, ls[j])# while not quotient % ls[j]:quotient //= ls[j]if quotient > 1:union(num, quotient)ans = 0count = [0 for _ in range(n)]for num in nums:parent_num = find(num)count[parent_num] += 1ans = max(ans, count[parent_num])return ans