深度强化学习（DRL）

本文是学习笔记，如有侵权，请联系删除。本文在ChatGPT辅助下完成。

参考链接

Deep Reinforcement Learning官方链接：https://github.com/wangshusen/DRL

源代码链接：https://github.com/DeepRLChinese/DeepRL-Chinese

B站视频：【王树森】深度强化学习(DRL)

豆瓣: 深度强化学习

Random Permutation（随机排列）

What is uniform random permutation?

排列数等于n!

“uniform random permutation”（均匀随机排列）是指生成一个排列，其中每个可能的排列都以相等的概率出现。具体来说，对于含有n个元素的集合，它的所有n!个排列中的每一个都有相同的概率被选中。

实现均匀随机排列的一种简单方法是 Fisher-Yates 洗牌算法。该算法基于迭代，从最后一个元素开始，每次随机选择当前位置及之前的一个位置，并将它们的元素交换。通过不断重复这个过程，最终得到一个均匀随机排列。

这种排列方法在各种应用中都很有用，例如在随机化算法、模拟实验和密码学中。在实际应用中，均匀随机排列通常要求具有良好的随机性质，以确保生成的排列满足统计学上的随机性要求。

Fisher-Yates Shuffle

Fisher-Yates Shuffle，又称为洗牌算法，是一种用于随机排列数组元素的有效且简单的算法。其目标是生成一个均匀随机的排列，即每个元素在排列中出现的概率相等。下面是Fisher-Yates Shuffle的详细步骤：

1. 初始化： 算法开始时，数组中的元素按照其原始顺序排列。

2. 迭代： 从数组的最后一个元素开始，依次向前迭代到第一个元素。

3. 随机选择： 对于当前迭代的位置（假设为i），生成一个[0, i]范围内的随机整数 j。

4. 交换元素： 将当前位置（i）的元素与随机选择位置（j）的元素进行交换。

5. 递减迭代： 继续迭代，减小当前位置，直到第一个元素。

通过这个过程，每个元素都有机会被选择到任何一个位置，而且每个位置被选择的概率是相等的。因此，经过足够的迭代次数后，数组中的元素将被洗牌成一个均匀随机的排列。

Fisher-Yates Shuffle是一种简单而强大的洗牌算法，广泛应用于计算机科学领域，尤其在实现随机算法、模拟实验和游戏开发等方面。

以下是使用Python实现Fisher-Yates Shuffle的简单代码：

import randomdef fisher_yates_shuffle(arr):# 从最后一个元素开始迭代for i in range(len(arr) - 1, 0, -1):# 生成随机索引，范围是 [0, i]j = random.randint(0, i)# 交换当前位置的元素与随机选择位置的元素arr[i], arr[j] = arr[j], arr[i]# 示例用法
my_array = [1, 2, 3, 4, 5]
fisher_yates_shuffle(my_array)
print(my_array)

这段代码使用了Python的random模块中的randint函数来生成随机整数。通过调用fisher_yates_shuffle函数，可以对任意数组进行Fisher-Yates Shuffle。在示例用法中，数组 [1, 2, 3, 4, 5] 被洗牌，打印结果可能是类似 [3, 5, 1, 4, 2] 的随机排列。

range(len(arr) - 1, 0, -1) 是一个用于生成迭代索引的 Python 内置函数 range 的调用。具体来说，这个函数的参数是起始值、结束值和步长。

• len(arr) - 1: 这是起始值，表示从数组的最后一个元素开始。
• 0: 这是结束值（不包含在范围内），表示索引递减至 0。
• -1: 这是步长，表示递减的步长为 1。

因此，range(len(arr) - 1, 0, -1) 生成了一个逆序的索引序列，从数组的最后一个元素开始递减到第一个元素。这个逆序的索引序列用于在 Fisher-Yates Shuffle 算法中迭代数组的位置。在每次迭代中，会随机选择一个之前的位置，并与当前位置的元素交换，从而完成洗牌的过程。

Fisher-Yates Shuffle 的时间复杂度是 O(n)，其中 n 是数组的长度。这是因为算法需要对数组中的每个元素进行一次迭代，并在每次迭代中进行一次交换。

Q学习算法

$\mathbb{Q}$学习算法上一节用 TD 算法训练 DQN（介绍DQN的笔记在这里：深度强化学习（王树森）笔记02）, 更准确地说，我们用的 TD 算法叫做 Q 学习算法 (Q- learning)。TD 算法是一大类算法，常见的有 Q 学习和 SARSA。Q 学习的目的是学到最优动作价值函数$Q_{\star }$,而 SARSA 的目的是学习动作价值函数$Q_{\pi }$。下一章会介绍 SARSA 算法。

Q 学习是在 1989 年提出的，而 DQN 则是 2013 年才提出。从 DQN 的名字 (深度 Q 网络)就能看出 DQN 与 Q 学习的联系。最初的 Q 学习都是以表格形式出现的。虽然表格形式的 Q 学习在实践中不常用，但还是建议读者有所了解。

用表格表示 $Q_{\star }:$

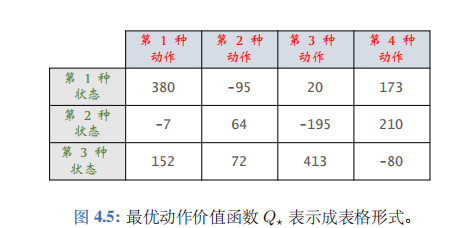
假设状态空间 $S$ 和动作空间 $\mathcal{A}$ 都是有限集，即集合中元素数量有限。 比如，$\mathcal{S}$中一共有3 种状态，$\mathcal{A}$中一共有 4 种动作。那么最优动作价值函数 $Q_{\star }(s,a)$ 可以表示为一个$3\times 4$ 的表格，比如右边的表格。基于当前状态 $s_t$,做决策时使用的公式
$$a_t={\mathrm{argmax}}_{a\in \mathcal{A}}{Q}_{\star }(s_t,a)$$

的意思是找到$s_t$ 对应的行(3 行中的某一行),找到该行最大的价值，返回该元素对应的动作。举个例子，当前状态$s_t$ 是第 2 种状态，那么我们查看第 2 行，发现该行最大的价值是 210, 对应第 4 种动作。那么应当执行的动作 $a_t$ 就是第 4 种动作。

该如何通过智能体的轨迹来学习这样一个表格呢？答案是用一个表格$\tilde{Q}$ 来近似 $Q_{\star }$。
首先初始化$\tilde{Q}$,可以让它是全零的表格。然后用表格形式的$\mathbb{Q}$学习算法更新$\tilde{Q}$,每次更新表格的一个元素。最终 $\tilde{Q}$ 会收敛到 $Q^{\star }$。

算法推导：

首先复习一下最优贝尔曼方程：
$$Q_{\star }(s_t,a_t)={\mathbb{E}}_{S_{t+1}\sim p(\cdot |s_t,a_t)}[R_t+\gamma \cdot \underset{A\in \mathcal{A}}{\max }{Q}_{\star }(S_{t+1},A)|S_t=s_t,A_t=a_t].$$

我们对方程左右两边做近似：

-方程左边的$Q_{\star }(s_t,a_t)$ 可以近似成$\tilde{Q}(s_t,a_t)$。$\tilde{Q}(s_t,a_t)$ 是表格在 $t$ 时刻对$Q_{\star }(s_t,a_{\iota })$ 做出的估计。
-方程右边的期望是关于下一时刻状态$S_{t+1}$求的。给定当前状态$s_t$, 智能体执行动作$a_t$,环境会给出奖励$r_t$ 和新的状态 $s_{t+1}$。用观测到的 $r_t$ 和 $s_{t+1}$ 对期望做蒙特卡洛近似，得到：

$$r_t+\gamma \cdot \underset{a\in \mathcal{A}}{\max }{Q}_{\star }(s_{t+1},a).(4.4)$$

-进一步把公式 (4.4) 中的$Q_{\star }$ 近似成$\tilde{Q}$, 得到

$${\hat{y}}_t\triangleq r_t+\gamma \cdot \underset{a\in \mathcal{A}}{\max }\tilde{Q}(s_{t+1},a).$$

把它称作 TD 目标。它是表格在 $t+1$ 时刻对 $Q_{\star }(s_t,a_t)$ 做出的估计。
$\tilde{Q}(s_t,a_t)$ 和${\hat{y}}_t$ 都是对最优动作价值$Q_{\star }(s_t,a_t)$ 的估计。由于${\hat{y}}_t$ 部分基于真实观测到的奖励$r_t$,我们认为${\hat{y}}_t$ 是更可靠的估计，所以鼓励$\tilde{Q}(s_t,a_t)$ 更接近${\hat{y}}_t$。更新表格$\tilde{Q}$中$(s_t,a_t)$ 位置上的元素：

$$\tilde{Q}(s_t,a_t)\leftarrow (1-\alpha )\cdot \tilde{Q}(s_t,a_t)+\alpha \cdot {\hat{y}}_t.$$

这样可以使得$\tilde{Q}(s_t,a_t)$ 更接近${\hat{y}}_t$。Q 学习的目的是让$\tilde{Q}$ 逐渐趋近于$Q_{\star }$。

收集训练数据：

$\mathbb{Q}$学习更新$\tilde{Q}$ 的公式不依赖于具体的策略。我们可以用任意策略控
制智能体，与环境交互，把得到的轨迹划分成 $(s_t,a_t,r_t,s_{t+1})$ 这样的四元组，存入经验回放数组。这个控制智能体的策略叫做行为策略(behavior policy), 比较常用的行为策略是 $ϵ$-greedy:
$$a_t=\{\begin{array}{ll}{\mathrm{argmax}}_a\tilde{Q}(s_t,a),& \text{以概率}(1-ϵ);\\ & \\ \text{均匀抽取}\mathcal{A}\text{中的一个动作},& \text{以概率}ϵ.\end{array}$$

事后用经验回放更新表格$\tilde{Q}$,可以重复利用收集到的四元组。
经验回放更新表格$\tilde{Q}:$

随机从经验回放数组中抽取一个四元组，记作$(s_j,a_j,r_j,s_{j+1})$。
设当前表格为${\tilde{Q}}_{\mathrm{now}}$。更新表格中$(s_j,a_j)$位置上的元素，把更新之后的表格记作 ${\tilde{Q}}_{\mathrm{new}}$。

1. 把表格 ${\tilde{Q}}_{\mathrm{now}}$ 中第 $(s_j,a_j)$ 位置上的元素记作：

$${\hat{q}}_j={\tilde{Q}}_{\mathrm{now}}(s_j,a_j).$$

2. 查看表格 ${\tilde{Q}}_{\mathrm{now}}$ 的第 $s_{j+1}$ 行，把该行的最大值记作：

$${\hat{q}}_{j+1}=\underset{a}{\max }{\tilde{Q}}_{\mathrm{now}}\left(s_{j+1},a\right).$$

3. 计算 TD 目标和 TD 误差：

$${\hat{y}}_j=r_j+\gamma \cdot {\hat{q}}_{j+1},{\delta }_j={\hat{q}}_j-{\hat{y}}_j.$$

4. 更新表格中 $(s_j,a_j)$ 位置上的元素：

$${\tilde{Q}}_{\mathrm{new}}(s_j,a_j)\leftarrow {\tilde{Q}}_{\mathrm{now}}(s_j,a_j)-\alpha \cdot {\delta }_j.$$

收集经验与更新表格$\tilde{Q}$可以同时进行。每当智能体执行一次动作，我们可以用经验回放对$\tilde{Q}$做几次更新。也可以每当完成一局游戏，对$\tilde{Q}$做几次更新。

同策略 (On-policy) 与异策略 (Off-policy)

在强化学习中经常会遇到两个专业术语：同策略(on-policy) 和异策略 (off-policy)。
为了解释同策略和异策略，我们要从行为策略 (behavior policy) 和目标策略 (target policy) 讲起。

在强化学习中，我们让智能体与环境交互，记录下观测到的状态、动作、奖励，用这些经验来学习一个策略函数。在这一过程中，控制智能体与环境交互的策略被称作行为策略。行为策略的作用是收集经验(experience),即观测的状态、动作、奖励。

强化学习的目的是得到一个策略函数，用这个策略函数来控制智能体。这个策略函数就叫做目标策略。在本章中，目标策略是一个确定性的策略，即用 DQN 控制智能体：

$$a_t=\underset{a}{\mathrm{argmax}}Q(s_t,a;\mathbf{w}).$$

本章的 Q 学习算法用任意的行为策略收集 $(s_t,a_t,r_t,s_{t+1})$ 这样的四元组，然后拿它们训练目标策略，即 DQN。介绍DQN的笔记在这里：深度强化学习（王树森）笔记02

行为策略和目标策略可以相同，也可以不同。同策略是指用相同的行为策略和目标策略，后面章节会介绍同策略。异策略是指用不同的行为策略和目标策略，本章的 DQN 属于异策略。同策略和异策略如图 4.6、4.7 所示。

由于DQN 是异策略，行为策略可以不同于目标策略，可以用任意的行为策略收集经验，比如最常用的行为策略是 $ϵ$-greedy:

$$a_t=\{\begin{array}{ll}{\mathrm{argmax}}_{a}Q(s_t,a;\mathbf{w}),& \text{以概率 }(1-ϵ);\\ \text{均匀抽取 }\mathcal{A}\text{中的一个动作},& \text{以概率 }ϵ.\end{array}$$

让行为策略带有随机性的好处在于能探索更多没见过的状态。在实验中，初始的时候让$ϵ$ 比较大 (比如 $ϵ=0.5)$; 在训练的过程中，让 $ϵ$逐渐衰减，在几十万步之后衰减到较小的值(比如 $ϵ=0.01)$, 此后固定住 $ϵ=0.01$ 。

异策略的好处是可以用行为策略收集经验，把$(s_t,a_t,r_t,s_{t+1})$ 这样的四元组记录到一个数组里，在事后反复利用这些经验去更新目标策略。这个数组被称作经验回放数组(replay buffer), 这种训练方式被称作经验回放 (experience replay)。注意，经验回放只适用于异策略，不适用于同策略，其原因是收集经验时用的行为策略不同于想要训练出的目标策略。

总结

DQN 是对最优动作价值函数$Q_{\star }$的近似。DQN 的输入是当前状态 $s_t$, 输出是每个动作的 Q 值。DQN 要求动作空间 $A$ 是离散集合，集合中的元素数量有限。如果动作空间$A$的大小是$k$,那么 DQN 的输出就是 $k$ 维向量。DQN 可以用于做决策，智能体执行 Q 值最大的动作。

TD 算法的目的在于让预测更接近实际观测。以驾车问题为例，如果使用 TD 算法，无需完成整个旅途就能做梯度下降更新模型。请读者理解并记忆 TD 目标、TD 误差的定义，它们将出现在所有价值学习的章节中。

Q 学习算法是 TD 算法的一种，可以用于训练 DQN。Q 学习算法由最优贝尔曼方程推导出。Q 学习算法属于异策略，允许使用经验回放。由任意行为策略收集经验， 存入经验回放数组。事后做经验回放，用 TD 算法更新 DQN 参数。

如果状态空间 $S$、动作空间 $A$ 都是较小的有限离散集合，那么可以用表格形式的Q学习算法学习$Q_{\star }$。如今表格形式的 Q 学习已经不常用。

SARSA 算法

TD 算法是一大类算法的总称。Q 学习是一种 TD 算法，Q 学习的目的是学习最优动作价值函数 $Q_{\star }$。这里介绍 SARSA, 它也是一种 TD 算法，SARSA 的目的是学习动作价值函数 $Q_{\pi }(s,a{)}_s$

表格形式的 SARSA

假设状态空间$S$ 和动作空间$\mathcal{A}$ 都是有限集，即集合中元素数量有限。比如，$S$ 中一共有 3 种状态，$\mathcal{A}$ 中一共有 4 种动作。那么动作价值函数 $Q_{\pi }(s,a)$ 可以表示为一个$3\times 4$ 的表格，比如右边的表格。该表格与一个策略函数$\pi (a|s)$ 相关联；如果 π 发生变化， 表格$Q_{\pi }$ 也会发生变化。

我们用表格$q$ 近似$Q_{\pi }$。该如何通过智能体与环境的交互来学习表格$q$呢？首先初始化$q$,可以让它是全零的表格。然后用表格形式的 SARSA 算法更新$q$, 每次更新表格的一个元素。最终$q$ 收敛到 $Q_{\pi }$。

推导表格形式的 SARSA 学习算法 :

SARSA 算法由下面的贝尔曼方程推导出：
$$Q_{\pi }(s_t,a_t)={\mathbb{E}}_{S_{t+1},A_{t+1}}[R_t+\gamma \cdot Q_{\pi }(S_{t+1},A_{t+1}\left)\right|S_t=s_t,A_t=a_t]$$

我们对贝尔曼方程左右两边做近似：
-方程左边的 $Q_{\pi }(s_t,a_t)$ 可以近似成 $q(s_t,a_t)$。$q(s_t,a_t)$ 是表格在 $t$ 时刻对 $Q_{\pi }(s_t,a_t)$ 做出的估计。
-方程右边的期望是关于下一时刻状态$S_{t+1}$ 和动作 $A_{t+1}$ 求的。给定当前状态 $s_t$, 智能体执行动作$a_t$,环境会给出奖励$r_t$ 和新的状态$s_{t+1}$。然后基于$s_{t+1}$做随机抽样， 得到新的动作
$${\tilde{a}}_{t+1}\sim \pi (\cdot |s_{t+1}).$$

用观测到的$r_t$、$s_{t+1}$ 和计算出的 ${\tilde{a}}_{t+1}$ 对期望做蒙特卡洛近似，得到：

$$r_t+\gamma \cdot Q_{\pi }(s_{t+1},{\tilde{a}}_{t+1}).(5.1)$$

-进一步把公式 (5.1) 中的 $Q_{\pi }$ 近似成 $q$, 得到

$${\hat{y}}_t\triangleq r_t+\gamma \cdot q(s_{t+1},{\tilde{a}}_{t+1}).$$

把它称作 TD 目标。它是表格在 $t+1$ 时刻对 $Q_{\pi }(s_t,a_t)$ 做出的估计。
$q(s_t,a_t)$ 和 ${\hat{y}}_t$ 都是对动作价值 $Q_{\pi }(s_t,a_t)$ 的估计。

由于 ${\hat{y}}_t$ 部分基于真实观测到的奖励 $r_t$ , 我们认为 ${\hat{y}}_t$ 是更可靠的估计，所以鼓励 $q(s_t,a_t)$ 趋近 ${\hat{y}}_t$。更新表格 $(s_t,a_t)$ 位置上的元素：

$$q(s_t,a_t)\leftarrow (1-\alpha )\cdot q(s_t,a_t)+\alpha \cdot {\hat{y}}_t.$$

这样可以使得 $q(s_t,a_t)$ 更接近 ${\hat{y}}_t$。

SARSA 是 State-Action-Reward-State-Action 的缩写，原因是 SARSA 算法用到了这个五元组$:(s_t,a_t,r_t,s_{t+1},{\tilde{a}}_{t+1})$。SARSA 算法学到的$q$ 依赖于策略 π, 这是因为五元组中的 ${\tilde{a}}_{t+1}$ 是根据 $\pi (\cdot |s_{t+1})$ 抽样得到的。

训练流程：

设当前表格为 $q_{\mathrm{now}}$, 当前策略为 ${\pi }_{\mathrm{now}}$。每一轮更新表格中的一个元素， 把更新之后的表格记作$q_{\mathrm{new}}$。

1. 观测到当前状态 $s_t$,根据当前策略做抽样$:a_t\sim {\pi }_{\mathrm{now}}(\cdot |s_t)$。
2. 把表格 $q_{\mathrm{now}}$ 中第 $(s_t,a_t)$ 位置上的元素记作：

$${\hat{q}}_t=q_{\mathrm{mow}}(s_t,a_t).$$

3. 智能体执行动作$a_t$之后，观测到奖励$r_t$ 和新的状态$s_{t+1}$。

4. 根据当前策略做抽样$:{\tilde{a}}_{t+1}\sim {\pi }_{\mathrm{now}}(\cdot |s_{t+1})$。注意，${\tilde{a}}_{t+1}$ 只是假想的动作，智能体不予执行。

5. 把表格 $q_{\mathrm{now}}$ 中第 $(s_{t+1},{\tilde{a}}_{t+1})$ 位置上的元素记作：

$${\hat{q}}_{t+1}=q_{\mathrm{now}}\left(s_{t+1},{\tilde{a}}_{t+1}\right).$$

6. 计算 TD 目标和 TD 误差：

$${\hat{y}}_t=r_t+\gamma \cdot {\hat{q}}_{t+1},{\delta }_t={\hat{q}}_t-{\hat{y}}_t.$$

7. 更新表格中 $(s_t,a_t)$ 位置上的元素：

$$q_{\mathrm{new}}(s_t,a_t)\leftarrow q_{\mathrm{now}}(s_t,a_t)-\alpha \cdot {\delta }_t.$$

8. 用某种算法更新策略函数。该算法与 SARSA 算法无关。

Q 学习与 SARSA 的对比：

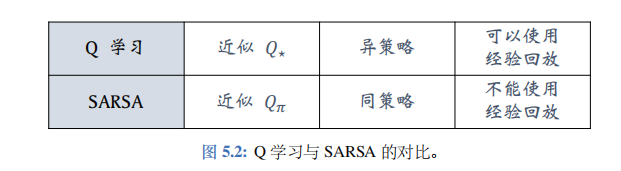
$\mathbb{Q}$ 学习不依赖于 π, 因此 $\mathbb{Q}$ 学习属于异策略 (off-policy), 可以用经验回放。而 SARSA 依赖于 π, 因此 SARSA 属于同策略(on-policy), 不能用经验回放。两种算法的对比如图 5.2 所示。

Q 学习的目标是学到表格 $\tilde{Q}$, 作为最优动作价值函数 $Q_{\star }$ 的近似。因为 $Q_{\star }$ 与 $\pi$ 无关，所以在理想情况下，不论收集经验用的行为策略$\pi$ 是什么，都不影响 Q 学习得到的最优动作价值函数。因此，$\mathbb{Q}$学习属于异策略(off-policy),允许行为策略区别于目标策略。Q 学习允许使用经验回放，可以重复利用过时的经验。

SARSA 算法的目标是学到表格$q$,作为动作价值函数$Q_{\pi }$ 的近似。$Q_{\pi }$ 与一个策略 $\pi$相对应，用不同的策略 $\pi$, 对应 $Q_{\pi }$ 就会不同。策略 $\pi$ 越好，$Q_{\pi }$ 的值越大。经验回放数组里的经验 $(s_j,a_j,r_j,s_{j+1})$ 是过时的行为策略 ${\pi }_{\mathrm{old}}$ 收集到的，与当前策略 ${\pi }_{\mathrm{now}}$ 应的价值 $Q_{{\pi }_{\mathrm{now}}}$ 对应不上。想要学习$Q_{\pi }$的话，必须要用与当前策略 ${\pi }_{\mathrm{now}}$ 收集到的经验，而不能用过时的${\pi }_{\mathrm{old}}$收集到的经验。这就是为什么 SARSA 不能用经验回放的原因。

神经网络形式的 SARSA

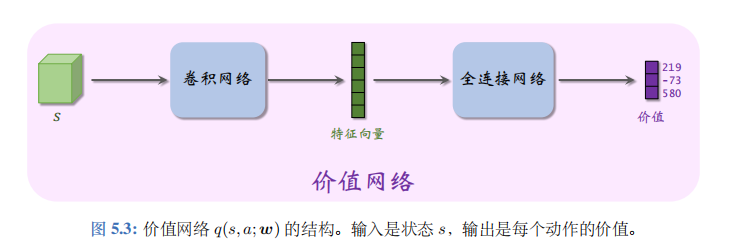
价值网络：

如果状态空间 $S$ 是无限集，那么我们无法用一张表格表示 $Q_{\pi }$, 否则表格的行数是无穷。一种可行的方案是用一个神经网络 $q(s,a;\mathbf{w})$ 来近似 $Q_{\pi }(s,a)$; 理想情况下，
$$q(s,a;\mathbf{w})=Q_{\pi }(s,a),\forall s\in \mathcal{S},a\in \mathcal{A}.$$

神经网络 $q(s,a;\mathbf{w})$ 被称为价值网络 (value network), 其中的 $w$ 表示神经网络中可训练的参数。神经网络的结构是人预先设定的 (比如有多少层，每一层的宽度是多少),而参数 $w$ 需要通过智能体与环境的交互来学习。首先随机初始化 $w$,然后用 SARSA 算法更新$w$。

神经网络的结构见图 5.3。价值网络的输入是状态 $s$。如果 $s$ 是矩阵或张量 (tensor), 那么可以用卷积网络处理$s$ (如图 5.3)。如果 $s$ 是向量，那么可以用全连接层处理 $s$。价值网络的输出是每个动作的价值。动作空间$A$ 中有多少种动作，则价值网络的输出就是多少维的向量，向量每个元素对应一个动作。举个例子，动作空间是 $A= { $左，右，上$} , $ 价值网络的输出是

$$\begin{array}{rlrl}& q(s,\text{ 左; }\mathbf{w})& =& 219,\\ & q(s,\text{ 右; }\mathbf{w})& =& -73,\\ & q(s,\text{ 上; }\mathbf{w})& =& 580.\end{array}$$

算法推导：

给定当前状态 $s_t$, 智能体执行动作 $a_t$, 环境会给出奖励 $r_t$ 和新的状态$s_{t+1}$。然后基于 $s_{t+1}$ 做随机抽样，得到新的动作 ${\tilde{a}}_{t+1}\sim \pi (\cdot |s_{t+1})$。定义 TD 目标：
$$\widehat{y_t}\triangleq r_t+\gamma \cdot q(s_{t+1},{\tilde{a}}_{t+1};\mathbf{w}).$$
我们鼓励$q(s_t,a_t;\mathbf{w})$ 接近 TD 目标 ${\hat{y}}_t$, 所以定义损失函数：

$$L(\mathbf{w})\triangleq \frac{1}{2}\left[q\right(s_t,a_t;\mathbf{w})-{\hat{y}}_t{]}^2.$$

损失函数的变量是 $w$,而 ${\hat{y}}_t$ 被视为常数。(尽管 ${\hat{y}}_t$ 也依赖于参数 $w$,但这一点被忽略掉。) 设${\hat{q}}_t=q(s_t,a_t;\mathbf{w})$。损失函数关于$w$ 的梯度是：

$$\begin{array}{rcl}{\nabla }_{\mathbf{w}}L(\mathbf{w})& =& \underset{\text{TD 误差 }{\delta }_t}{\underbrace{\left({\hat{q}}_t-{\hat{y}}_t\right)}}\cdot {\nabla }_{\mathbf{w}}q(s_t,a_t;\mathbf{w}).\end{array}$$
做一次梯度下降更新 $w:$

$$\mathbf{w}\leftarrow \mathbf{w}-\alpha \cdot {\delta }_t\cdot {\nabla }_{\mathbf{w}}q(s_t,a_t;\mathbf{w}).$$

这样可以使得 $q(s_t,a_t;\mathbf{w})$ 更接近 ${\hat{y}}_t$。此处的 $\alpha$ 是学习率，需要手动调整。

训练流程：

设当前价值网络的参数为 $w_{\mathrm{now}}$, 当前策略为 ${\pi }_{\mathrm{now}}$。每一轮训练用五元组 $(s_t,a_t,r_t,s_{t+1},{\tilde{a}}_{t+1})$ 对价值网络参数做一次更新。

1. 观测到当前状态 $s_t$,根据当前策略做抽样：$a_t\sim {\pi }_{\mathrm{now}}(\cdot |s_t)$。
2. 用价值网络计算 $(s_t,a_t)$ 的价值：

$$\widehat{q_t}=q(s_t,a_t;{\mathbf{w}}_{\mathrm{now}}).$$

3. 智能体执行动作 $a_t$ 之后，观测到奖励 $r_t$ 和新的状态 $s_{t+1}$。
   4.根据当前策略做抽样$:{\tilde{a}}_{t+1}\sim {\pi }_{\mathrm{now}}(\cdot |s_{t+1})$。注意，${\tilde{a}}_{t+1}$ 只是假想的动作，智能体不予执行。
4. 用价值网络计算 $(s_{t+1},{\tilde{a}}_{t+1})$ 的价值：

$${\hat{q}}_{t+1}=q(s_{t+1},{\tilde{a}}_{t+1};{\mathbf{w}}_{\mathrm{now}}).$$

6. 计算 TD 目标和 TD 误差：

$${\hat{y}}_t=r_t+\gamma \cdot {\hat{q}}_{t+1},{\delta }_t={\hat{q}}_t-{\hat{y}}_t.$$

7.对价值网络$q$ 做反向传播，计算 $q$ 关于 $w$ 的梯度：${\nabla }_{\mathbf{w}}q(s_t,a_t;{\mathbf{w}}_{\mathrm{now}})$ 。

8. 更新价值网络参数：

$$w_{\mathrm{new}}\leftarrow w_{\mathrm{now}}-\alpha \cdot {\delta }_t\cdot {\nabla }_{\mathbf{w}}q(s_t,a_t;{\mathbf{w}}_{\mathrm{now}}).$$

9. 用某种算法更新策略函数。该算法与 SARSA 算法无关。

多步 TD 目标

首先回顾一下 SARSA 算法。给定五元组 $(s_t,a_t,r_t,s_{t+1},a_{t+1})$, SARSA 计算 TD 目标：
$$\widehat{y_t}=r_t+\gamma \cdot q(s_{t+1},a_{t+1};\mathbf{w}).$$

公式中只用到一个奖励$r_t$,这样得到的${\hat{y}}_t$ 叫做单步 TD 目标。多步 TD 目标用 $m$ 个奖励可以视作单步 TD 目标的推广。下面我们推导多步 TD 目标。

数学推导：

设一局游戏的长度为 $n$。根据定义，$t$ 时刻的回报 $U_t$ 是 $t$ 时刻之后的所有奖励的加权和：
$$U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\cdots +{\gamma }^{n-t}{R}_n.$$

同理，$t+m$ 时刻的回报可以写成：

$$U_{t+m}=R_{t+m}+\gamma R_{t+m+1}+{\gamma }^2{R}_{t+m+2}+\cdots +{\gamma }^{n-t-m}{R}_n.$$

下面我们推导两个回报的关系。把$U_t$ 写成：

$$\begin{array}{rcl}{U}_t& =& \left(R_t+\gamma R_{t+1}+\cdots +{\gamma }^{m-1}{R}_{t+m-1}\right)+\left({\gamma }^m{R}_{t+m}+\cdots +{\gamma }^{n-t}{R}_n\right)\\ & =& \left({\sum }_{i=0}^{m-1}{\gamma }^i{R}_{t+i}\right)+{\gamma }^m\underset{\text{等于}{U}_{t+m}}{\underbrace{\left(R_{t+m}+\gamma R_{t+m+1}+\cdots +{\gamma }^{n-t-m}{R}_n\right)}}.\end{array}$$
因此，回报可以写成这种形式：

$$U_t=\left(\sum _{i=0}^{m-1}{\gamma }^i{R}_{t+i}\right)+{\gamma }^m{U}_{t+m}.(5.2)$$
动作价值函数$Q_{\pi }(s_t,a_t)$ 是回报$U_t$ 的期望，而$Q_{\pi }(s_{t+m},a_{t+m})$是回报$U_{t+m}$的期望。利用公式 (5.2), 再按照贝尔曼方程的证明 , 不难得出下面的定理：

设 $R_k$ 是 $S_k,A_k.$ $S_{k+1}$ 的函数，$\forall k=1,\cdots ,n$。那么

$$\underset{U_t\text{的期望}}{\underbrace{Q_{\pi }\left(s_t,a_t\right)}}=\mathbb{E}[\left(\sum _{i=0}^{m-1}{\gamma }^i{R}_{t+i}\right)+{\gamma }^m\cdot \underset{U_{t+m}\text{的期望}}{\underbrace{Q_{\pi }\left(S_{t+m},A_{t+m}\right)}}|S_t=s_t,A_t=a_t].$$

公式中的期望是关于随机变量$S_{t+1},A_{t+1},\cdots ,S_{t+m},A_{t+m}$求的。

注 回报 $U_t$ 的随机性来自于$t$ 到 $n$ 时刻的状态和动作：

$$S_t,A_t,S_{t+1},A_{t+1},\cdots ,S_{t+m},A_{t+m},S_{t+m+1},A_{t+m+1},\cdots ,S_n,A_n.$$

定理中把$S_t=s_t$ 和$A_t=a_t$看做是观测值，用期望消掉 $S_{t+1},A_{t+1},\cdots ,S_{t+m},A_{t+m}$,而$Q_{\pi }(S_{t+m},A_{t+m})$ 则消掉了剩余的随机变量$S_{t+m+1},A_{t+m+1},\cdots ,S_n,A_n$。

多步 TD目标：

我们对定理 5.1 中的期望做蒙特卡洛近似，然后再用价值网络$q(s,a;\mathbf{w})$ 近似动作价值函数 $Q_{\pi }(s,a)$。具体做法如下：

• 在$t$ 时刻，价值网络做出预测${\hat{q}}_t=q(s_t,a_t;\mathbf{w})$,它是对$Q_{\pi }(s_t,a_t)$ 的估计。

• 已知当前状态$s_t$,用策略$\pi$控制智能体与环境交互$m$ 次，得到轨迹

$$r_t,s_{t+1},a_{t+1},r_{t+1},\cdots ,s_{t+m-1},a_{t+m-1},r_{t+m-1},s_{t+m},a_{t+m}.$$

在$t+m$ 时刻，用观测到的轨迹对定理 5.1 中的期望做蒙特卡洛近似，把近似的结果记作：

$\left({\sum }_{i=0}^{m-1}{\gamma }^i{r}_{t+i}\right)+{\gamma }^m\cdot Q_{\pi }\left(s_{t+m},a_{t+m}\right).$

• 进一步用$q(s_{t+m},a_{t+m};\mathbf{w})$近似$Q_{\pi }(s_{t+m},a_{t+m})$,得到：

$$\widehat{y_t}\triangleq \left(\sum _{i=0}^{m-1}{\gamma }^i{r}_{t+i}\right)+{\gamma }^m\cdot q(s_{t+m},a_{t+m};\mathbf{w}).$$

把${\hat{y}}_t$ 称作 $m$ 步TD 目标。

${\hat{q}}_t=q(s_t,a_t;\mathbf{w})$ 和 ${\hat{y}}_t$ 分别是价值网络在 $t$ 时刻和 $t+m$ 时刻做出的预测，两者都是对$Q_{\pi }(s_t,a_t)$ 的估计值。${\hat{q}}_t$ 是纯粹的预测，而${\hat{y}}_t$ 则基于 $m$ 组实际观测，因此 ${\hat{y}}_t$ 比 ${\hat{q}}_t$ 更可靠。我们鼓励${\hat{q}}_t$ 接近${\hat{y}}_t$。设损失函数为
$$L(\mathbf{w})\triangleq \frac{1}{2}\left[q\right(s_t,a_t;\mathbf{w})-{\hat{y}}_t{]}^2.(5.3)$$

做一步梯度下降更新价值网络参数 $w$:

$$\mathbf{w}\leftarrow \mathbf{w}-\alpha \cdot \left({\hat{q}}_t-{\hat{y}}_t\right)\cdot {\nabla }_{\mathbf{w}}q(s_t,a_t;\mathbf{w}).$$
训练流程：

设当前价值网络的参数为 $w_{\mathrm{now}}$, 当前策略为 ${\pi }_{\mathrm{now}}$。执行以下步骤更新价值网络和策略。

1. 用策略网络 ${\pi }_{\mathrm{now}}$ 控制智能体与环境交互，完成一个回合，得到轨迹：

$$\begin{array}{r}{s}_1,a_1,r_1,s_2,a_2,r_2,\cdots ,s_n,a_n,r_n.\end{array}$$

2. 对于所有的$t=1,\cdots ,n-m$, 计算

$${\hat{q}}_t=q(s_t,a_t;{\mathbf{w}}_{\mathrm{now}}).$$

3.对于所有的$t=1,\cdots ,n-m$,计算多步 TD 目标和 TD 误差：

$$\widehat{y_t}=\sum _{i=0}^{m-1}{\gamma }^i{r}_{t+i}+{\gamma }^m{\hat{q}}_{t+m},{\delta }_t={\hat{q}}_t-{\hat{y}}_t.$$

4. 对于所有的 $t=1,\cdots ,n-m$, 对价值网络 $q$ 做反向传播，计算 $q$ 关于 $w$ 的梯度：

$${\nabla }_{\mathbf{w}}q(s_t,a_t;{\mathbf{w}}_{\mathbf{now}}).$$

5. 更新价值网络参数：

$$w_{\mathrm{new}}\leftarrow w_{\mathrm{now}}-\alpha \cdot \sum _{t=1}^{n-m}{\delta }_t\cdot {\nabla }_{\mathbf{w}}q(s_t,a_t;{\mathbf{w}}_{\mathrm{now}}).$$

6. 用某种算法更新策略函数 $\pi$。该算法与 SARSA 算法无关。

蒙特卡洛与自举

上一节介绍了多步 TD 目标。单步 TD 目标、回报是多步 TD 目标的两种特例。如下图所示，如果设$m=1$,那么多步 TD 目标变成单步 TD 目标。如果设 $m=n-t+1$,那么多步 TD 目标变成实际观测的回报 $u_t$ 。

蒙特卡洛
训练价值网络 $q(s,a;\mathbf{w})$ 的时候，我们可以将一局游戏进行到底，观测到所有的奖励$r_1,\cdots ,r_n$,然后计算回报$u_t={\sum }_{i=0}^{n-t}{\gamma }^i{r}_{t+i}$。拿$u_t$ 作为目标，鼓励价值网络 $q(s_t,a_t;\mathbf{w})$ 接近$u_t$。定义损失函数：
$$L(\mathbf{w})=\frac{1}{2}{\left[q(s_t,a_t;\mathbf{w})-u_t\right]}^2.$$

然后做一次梯度下降更新 $w$:

$$w\leftarrow w-\alpha \cdot {\nabla }_{\mathbf{w}}L(\mathbf{w}),$$

这样可以让价值网络的预测 $q(s_t,a_t;\mathbf{w})$ 更接近 $u_t$。这种训练价值网络的方法不是 TD。

在强化学习中，训练价值网络的时候以$u_t$作为目标，这种方式被称作“蒙特卡洛”。原因是这样的，动作价值函数可以写作$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$,而我们用实际观测 $u_t$ 去近似期望，这就是典型的蒙特卡洛近似。

蒙特卡洛的好处是无偏性$:u_t$ 是$Q_{\pi }(s_t,a_t)$ 的无偏估计。由于 $u_t$ 的无偏性，拿 $u_t$ 作为目标训练价值网络，得到的价值网络也是无偏的。

蒙特卡洛的坏处是方差大。随机变量$U_t$ 依赖于 $S_{t+1},A_{t+1},\cdots ,S_n,A_n$ 这些随机变量，其中不确定性很大。观测值$u_t$ 虽然是$U_t$ 的无偏估计，但可能实际上离 E { U t } \mathbb{E}\{U_t\} E{Ut​} 很远。
因此，拿$u_t$ 作为目标训练价值网络，收敛会很慢。

自举
在介绍价值学习的自举之前，先解释一下什么叫自举。大家可能经常在强化学习和统计学的文章里见到 bootstrapping 这个词。它的字面意思是“拔自己的鞋带，把自己举起来”。所以 bootstrapping 翻译成“自举”, 即自己把自己举起来。自举听起来很荒谬。即使你“力拔山兮气盖世”,你也没办法拔自己的鞋带，把自己举起来。虽然自举乍看起来不现实，但是在统计和机器学习是可以做到自举的；自举在统计和机器学习里面非常常用。
在强化学习中，“自举”的意思是“用一个估算去更新同类的估算”,类似于“自己把自己给举起来”。SARSA 使用的单步 TD 目标定义为：

SARSA 鼓励 $q(s_t,a_t;w)$ 接近${\hat{y}}_t$, 所以定义损失函数

$${\hat{y}}_t=r_t+\underset{\text{价值网络做出的估计}}{\underbrace{\gamma \cdot q(s_{t+1},a_{t+1};\mathbf{w})}}.$$

$$\begin{array}{rcl}L(\mathbf{w})& =& \frac{1}{2}[\underset{\text{让价值网络拟合 }\hat{y}t}{\underbrace{q(s_t,a_t;\mathbf{w})-{\hat{y}}_t}}{]}^2.\end{array}$$

TD 目标${\hat{y}}_t$ 的一部分是价值网络做出的估计 $\gamma \cdot q(s_{t+1},a_{t+1};\mathbf{w})$,然后 SARSA 让$q(s_t,a_t;\mathbf{w})$ 去拟合 ${\hat{y}}_t$。这就是用价值网络自己做出的估计去更新价值网络自己，这属于“自举”。(严格地说，TD 目标 ${\hat{y}}_t$ 中既有自举的成分，也有蒙特卡洛的成分。TD 目标中的 $\gamma \cdot q(s_{t+1},a_{t+1};w)$ 是自举， 因为它拿价值网络自己的估计作为目标。TD 目标中的 $r_t$ 是实际观测，它是对 $\mathbb{E}[R_t]$ 的蒙特卡洛。)

自举的好处是方差小。单步 TD 目标的随机性只来自于 $S_{t+1}$ 和 $A_{t+1}$, 而回报 $U_t$ 的随机性来自于$S_{t+1},A_{t+1},\cdots ,S_n,A_n$。很显然，单步 TD 目标的随机性较小，因此方差较小。用自举训练价值网络，收敛比较快。

自举的坏处是有偏差。价值网络$q(s,a;\mathbf{w})$ 是对动作价值$Q_{\pi }(s,a)$ 的近似。最理想的情况下，$q(s,a;\mathbf{w})=Q_{\pi }(s,a)$,$\forall s,a$。假如碰巧$q(s_{j+1},a_{j+1};\mathbf{w})$低估(或高估)真实价值$Q_{\pi }(s_{j+1},a_{j+1})$,则会发生下面的情况：

$$\begin{array}{cccc}& q(s_{j+1},a_{j+1};\mathbf{w})& \text{低估(或高估)}& Q_{\pi }(s_{j+1},a_{j+1})\\ ⟹& \widehat{y_j}& \text{低估(或高估)}& Q_{\pi }(s_j,a_j)\\ ⟹& q(s_j,a_j;\mathbf{w})& \text{低估(或高估)}& Q_{\pi }(s_j,a_j).\end{array}$$

也就是说，自举会让偏差从 $(s_{t+1},a_{t+1})$ 传播到 $(s_t,a_t)$。后面详细讨论自举造成的偏差以及解决方案。

蒙特卡洛和自举的对比
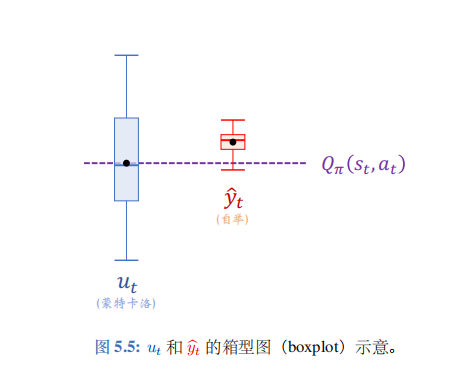
在价值学习中，用实际观测的回报 $u_t$ 作为目标的方法被称为蒙特卡洛，即图 5.5 中的蓝色的箱型图。$u_t$ 是 $Q_{\pi }(s_t,a_t)$ 的无偏估计，即 $U_t$ 的期望等于$Q_{\pi }(s_t,a_t)$。但是它的方差很大，也就是说实际观测到的$u_t$可能离$Q_{\pi }(s_t,a_t)$ 很远。

用单步 TD 目标 ${\hat{y}}_t$ 作为目标的方法被称为自举，即图5.5 中的红色的箱型图。自举的好处在于方差小，${\hat{y}}_t$不会 偏离期望太远。但是${\hat{y}}_t$ 往往是有偏的， 它的期望往往不等于$Q_{\pi }(s_t,a_t)$。用自举训练出的价值网络往往有系统性的偏差 (低估或者高估)。实践中，自举通常比蒙特卡洛收敛更快，这就是为什么训练 DQN 和价值网络通常用 TD 算法。

如图 5.4 所示，多步 TD 目标 ${\hat{y}}_t=({\sum }_{i=0}^{m-1}{\gamma }^i{r}_{t+i})+{\gamma }^m\cdot q(s_{t+m},a_{t+m};w)$ 介于蒙特卡洛和自举之间。多步 TD 目标有很大的蒙特卡洛成分，其中的${\sum }_{i=0}^{m-1}{\gamma }^i{r}_{t+i}$ 基于 $m$ 个实际观测到的奖励。多步 TD 目标也有自举的成分，其中的 ${\gamma }^m\cdot q(s_{t+m},a_{t+m};w)$ 是用价值网络自己算出来的。如果把$m$ 设置得比较好，可以在方差和偏差之间找到好的平衡，使得多步 TD 目标优于单步 TD 目标，也优于回报 $u_t$。

后记

截至2024年1月28日21点02分，学习完Q learning和SARSA算法，主要依据王树森的《深度强化学习》这本书做的笔记。