单链表

题目链接：826. 单链表 - AcWing题库
思路：AcWing 826. 单链表---图解 - AcWing

需要注意的点在于理解ne[idx] = head，idx表示当前的点，意思是将当前的点链到头结点的后面，再将头结点链在当前idx的前面。

#include<bits/stdc++.h>using namespace std;
const int N = 100010;
int head, e[N], ne[N], idx;// 初始化
void init()
{head = -1;idx = 0;
}// 在链表头插入一个数a
void insert_to_head(int a)
{e[idx] = a;ne[idx] = head;head = idx ++ ;
}void insert(int k,int a)
{e[idx] = a;ne[idx] = ne[k];ne[k] = idx ++ ;
}// 将头结点删除，需要保证头结点存在
void remove(int k)
{ne[k] = ne[ne[k]];
}int main(){int m;cin>>m;init();while(m--){char a;cin>>a;int k,x;if(a=='H'){cin>>x;insert_to_head(x);}else if(a=='I'){cin>>k>>x;insert(k-1,x);}else{cin>>k;if(!k) head = ne[head];else remove(k-1);}}for(int i=head;i!=-1;i=ne[i]) cout<<e[i]<<" ";return 0;
}

双链表

题目链接：827. 双链表 - AcWing题库

思路：这个博客写的可好AcWing 827. 双链表 - AcWing。

需要注意的地方在于r数组和l数组的含义。r[idx]表示的是idx的右边，l[idx]表示idx的左边，开始时初始化0的左边是1，1的右边是左，所以r[0] = 1,l[1] = 0。

#include<bits/stdc++.h>using namespace std;const int N = 100010;int e[N], l[N], r[N], idx;// 初始化
void init()
{//0是左端点，1是右端点r[0] = 1, l[1] = 0;idx = 2;
}// 在节点a的右边插入一个数x
void insert(int a, int x)
{e[idx] = x;l[idx] = a, r[idx] = r[a];l[r[a]] = idx, r[a] = idx ++ ;
}// 删除节点a
void remove(int a)
{l[r[a]] = l[a];r[l[a]] = r[a];
}int main(){int m;cin>>m;init();while(m--){string op;cin>>op;int k,x;if(op[0] == 'L'){cin>>x;insert(0,x);}else if(op[0] == 'R'){cin>>x;insert(l[1],x);}else if(op[0] == 'D'){cin>>k;remove(k+1);}else if(op[1] == 'L'){cin>>k>>x;insert(l[k+1],x);}else{cin>>k>>x;insert(k+1,x);}}for(int i=r[0];i!=1;i=r[i]){cout<<e[i]<<" ";}return 0;
}

栈的应用

题目链接：3302. 表达式求值 - AcWing题库
思路：这个题解写的很好AcWing 3302. 表达式求值：多图讲解运算符优先级+详细代码注释 - AcWing。

主要的思路在符号栈上，符号栈内存储的符号优先级一定递增，即将进来的符号若小于当前栈顶优先级，则先对栈内高优先级符号进行运算，直到栈顶优先级低于待入栈符号优先级。

还需要注意的是，对于相同运算符来说，栈内的优先级大于栈外优先级，即遇到栈顶是一个加号，待入栈也是一个加号，先运算栈内加号，当栈为空或遇到更低优先级的符号时再将栈外加号入栈。

#include<bits/stdc++.h>using namespace std;
stack<int> num;
stack<int> op;unordered_map<char,int> h{{'+',1},{'-',1},{'*',2},{'/',2}};
void calc(){char ops = op.top();op.pop();int b = num.top();num.pop();int a = num.top();num.pop();if(ops == '+') num.push(a+b);if(ops == '-') num.push(a-b);if(ops == '*') num.push(a*b);if(ops == '/') num.push(a/b);return;
}int main(){string s;cin>>s;for(int i=0;i<s.size();i++){if(isdigit(s[i])){  //遇到数字的情况int j = i;int val = 0;while(j<s.size()&&isdigit(s[j])){val = val*10 + s[j] - '0';j++;}i=j-1;num.push(val);}else{  //遇到字符的情况if(s[i] == '(') op.push('(');else if(s[i] == ')'){while(op.top()!='('){calc();}op.pop();}else{while(op.size() && h[op.top()] >= h[s[i]]){calc();}op.push(s[i]);}}}while(op.size())calc();cout<<num.top()<<endl;return 0;
}

单调栈

题目链接：830. 单调栈 - AcWing题库

思路：维护一个数字单调递增的栈，若下一个待入栈数字小于栈顶时，持续出栈。感觉跟表达式求值中栈内优先级高于栈外优先级有点像，hh。

常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{while (tt && check(stk[tt], i)) tt -- ;stk[ ++ tt] = i;
}

#include<bits/stdc++.h>using namespace std;
const int N = 100010;
int a[N];
int main(){int n;cin>>n;stack<int> stk;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<n;i++){while(stk.size()&&stk.top() >= a[i]) stk.pop();if(stk.size()) cout<<stk.top()<<" ";else cout<<-1<<" ";stk.push(a[i]);}return 0;
}

单调队列

题目链接：154. 滑动窗口 - AcWing题库
思路：排在后面的数字越小/大，越优秀，当这样的元素出现时，将右侧队列中的元素出队。由于要求队列能右侧出队，所以需要自己模拟队列（感觉可以使用双端队列实现）。

需要注意的点是队列中存储的是下标，是为了方便队头出队。

#include<bits/stdc++.h>using namespace std;
const int N = 1e6+10;int a[N];
int q[N];
int main(){int n,k;cin>>n>>k;for(int i=0;i<n;i++) cin>>a[i];int h=1,t=0;for(int i=0;i<n;i++){while(h<=t&&a[q[t]] >= a[i]) t--;q[++t] = i;if(q[h]<i-k+1) h++;if(i>=k-1) cout<<a[q[h]]<<" ";}h=1;t=0;cout<<endl;for(int i=0;i<n;i++){while(h<=t&&a[q[t]] <= a[i]) t--;q[++t] = i;if(q[h]<i-k+1) h++;if(i>=k-1) cout<<a[q[h]]<<" ";}return 0;
}

KMP

题目链接：831. KMP字符串 - AcWing题库

思路：对于模板串（短串）进行初始化ne数组，ne数组表示当前位置不匹配时，可以从哪个位置开始匹配。具体思路太复杂，放弃，可以考虑直接背过。时间复杂度为O(m+n)。

#include<bits/stdc++.h>using namespace std;const int N = 1e5+10;
const int M = 1e6+10;
char p[N],s[M];
int ne[M];
void init(char p[],int n,int m){// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度for (int i = 2, j = 0; i <= n; i ++ ){while (j && p[i] != p[j + 1]) j = ne[j];if (p[i] == p[j + 1]) j ++ ;ne[i] = j;}
}int main(){int n,m;cin>>n;cin>>p+1;cin>>m;cin>>s+1;init(p,n,m);// 匹配for (int i = 1, j = 0; i <= m ;i ++ ){while (j && s[i] != p[j + 1]) j = ne[j];if (s[i] == p[j + 1]) j ++ ;if (j == n){cout<<i-n<<' ';j = ne[j];// 匹配成功后的逻辑}}return 0;
}

Trie（字典树）

题目链接：835. Trie字符串统计 - AcWing题库
思路：ch[0][2]=1表示从0号结点开始往2('c')走能走到1号节点。

#include<bits/stdc++.h>using namespace std;
const int N = 100010;
int son[N][26],cnt[N],idx = 1;void insert(string s){int p = 0;for(int i=0;i<s.size();i++){int u = s[i] - 'a';if(!son[p][u]) son[p][u] = idx++;p = son[p][u];}cnt[p]++;
}int query(string s){int p = 0;for(int i=0;i<s.size();i++){int u = s[i] - 'a';if(!son[p][u]) return 0;p = son[p][u];}return cnt[p];
}int main(){int n;cin>>n;while(n--){char op;string s;cin>>op>>s;if(op == 'I'){insert(s);}else cout<<query(s)<<endl;}return 0;
}

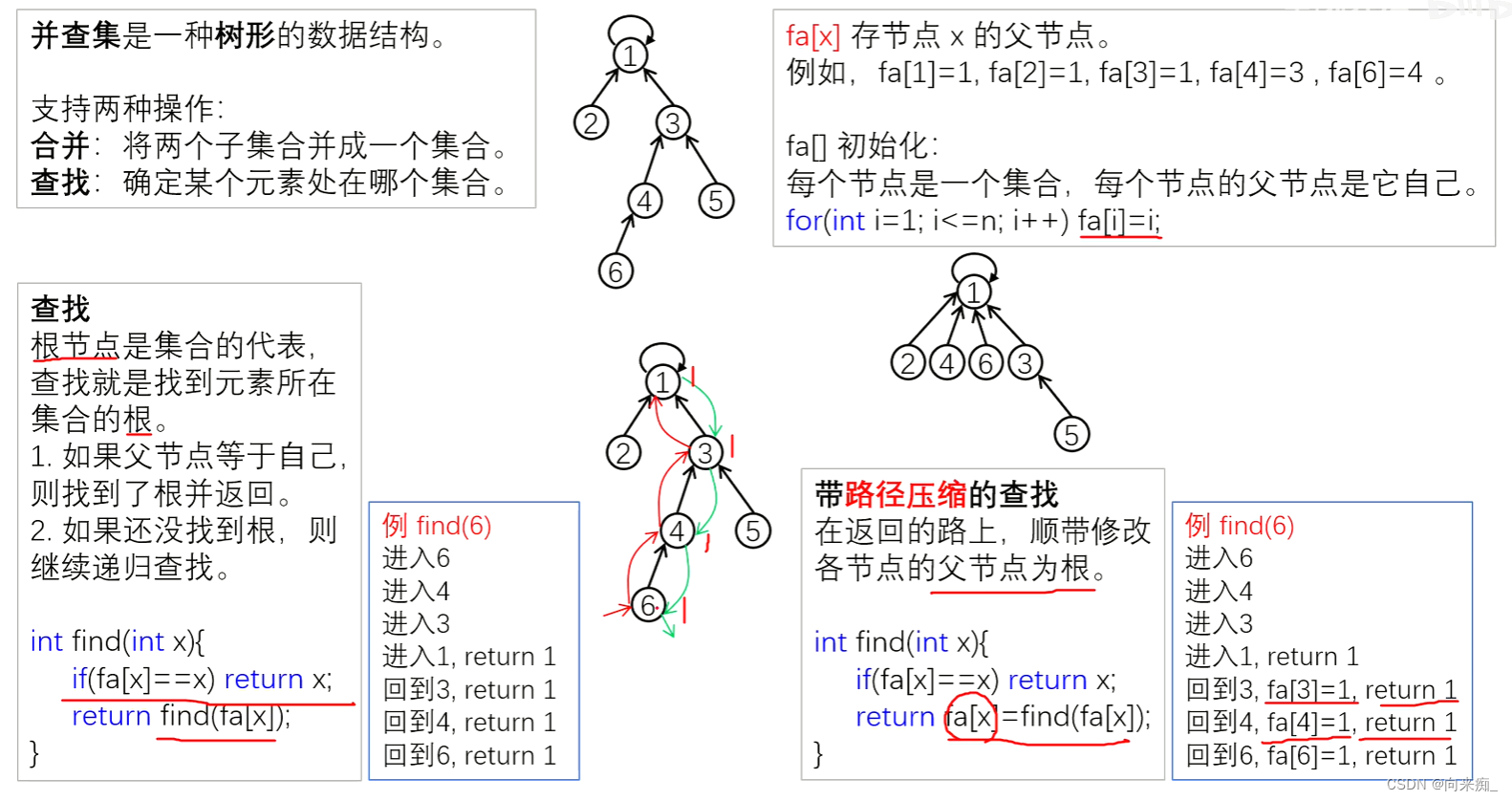
并查集

题目链接：836. 合并集合 - AcWing题库

思路：fa[i]表示i节点的父亲节点。开始时每个节点的父亲节点都是自己。

#include<bits/stdc++.h>using namespace std;
const int N= 1e5+10;int fa[N];  //下标表示当前点，数组值表示其父亲节点的下标int find(int x){if(fa[x] == x) return x;return fa[x] = find(fa[x]);
}void unionset(int x,int y){fa[find(x)] = find(y); 
}int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++) fa[i] = i;while(m--){char op;cin>>op;int x,y;cin>>x>>y;if(op == 'M'){unionset(x,y);}else{if(find(x) == find(y)) cout<<"Yes"<<endl;else cout<<"No"<<endl;}}return 0;
}

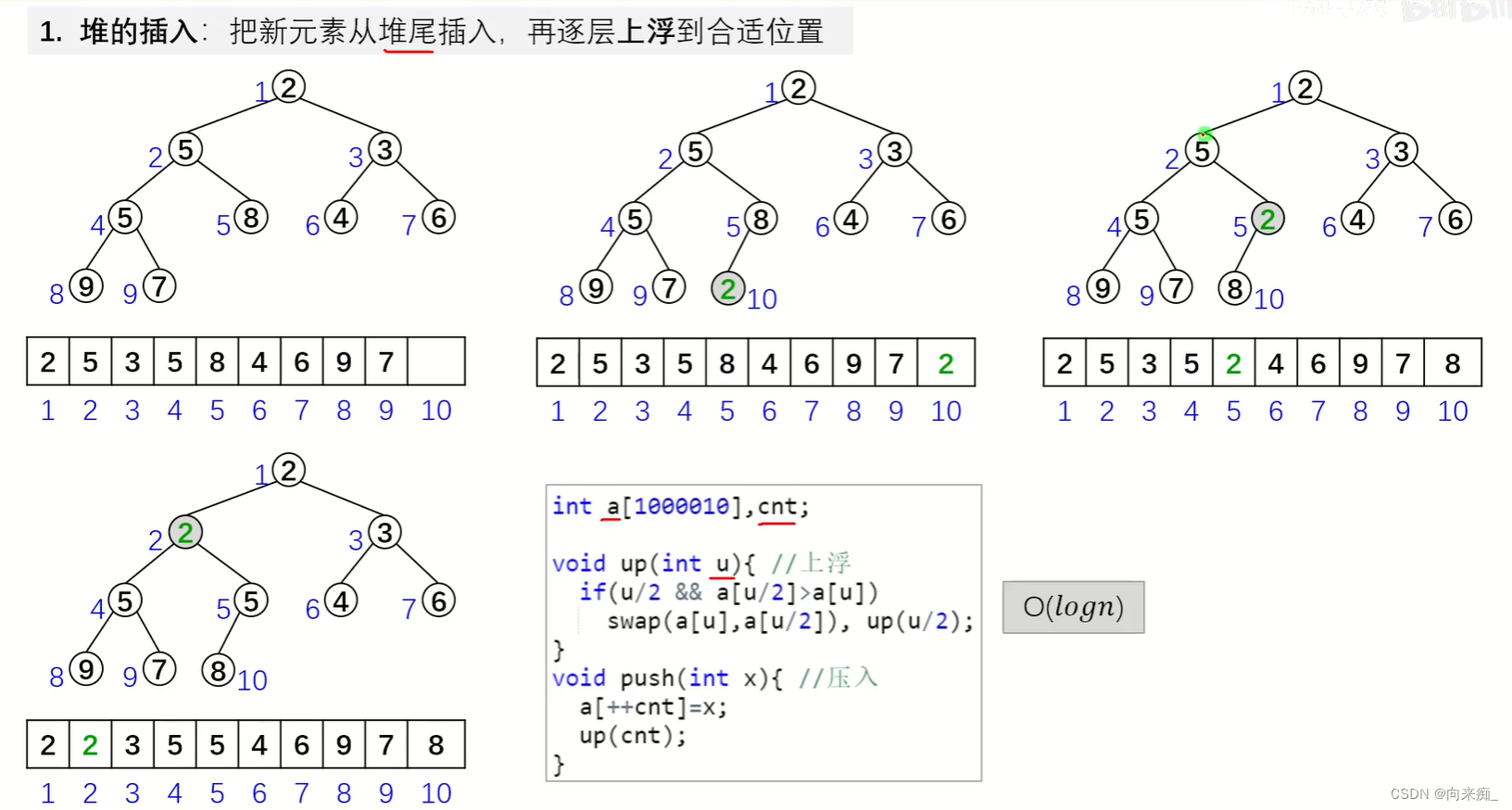
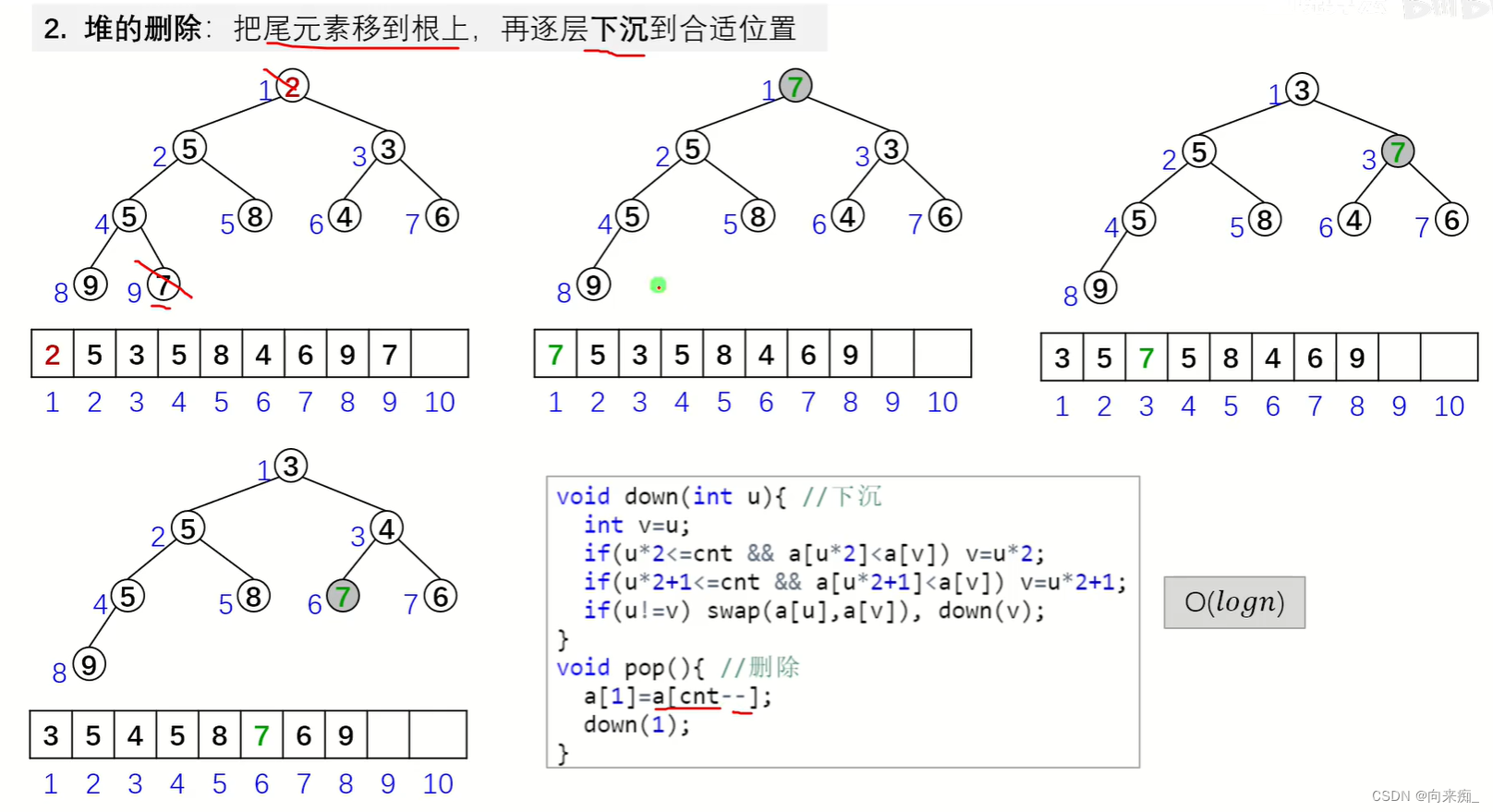
堆

题目链接：838. 堆排序 - AcWing题库

思路：主要的操作包括up和down，up表示将节点上移，一般在新节点进入时使用，down表示将节点下移，一般在删除元素时使用。

需要注意的点在于一些小细节，例如递归边界，up和down都使用递归的形式，需要注意什么时候递归停止或是什么时候采用递归。

#include<bits/stdc++.h>using namespace std;
const int N = 100010;
int a[N];
int cnt;
void up(int x){if(x/2&&a[x]<a[x/2]){swap(a[x],a[x/2]);up(x/2);}
}void down(int x){int u = x;if(x*2<=cnt&&a[u]>a[x*2]) u = x*2;if(x*2+1<=cnt&&a[u]>a[x*2+1]) u = x*2+1;if(x!=u){swap(a[x],a[u]);down(u);}
}int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++) {cin>>a[++cnt];up(cnt);}// for(int i=1;i<=cnt;i++) cout<<a[i]<<" ";// cout<<endl;while(m--){cout<<a[1]<<" ";swap(a[1],a[cnt]);cnt--;down(1);// for(int i=1;i<=cnt;i++) cout<<a[i]<<" ";// cout<<endl;}return 0;
}

哈希表

题目链接：841. 字符串哈希 - AcWing题库

思路：

#include<bits/stdc++.h>using namespace std;
const int N = 100010;
typedef unsigned long long ULL;
ULL h[N],p[N];
int P = 131;
ULL getSeg(int l,int r){return h[r] - h[l-1] * p[r-l+1];
}
int main(){int n,m;cin>>n>>m;char s[N];cin>>s+1;p[0] = 1;for(int i=1;i<=n;i++){h[i] = h[i-1]*P + s[i];p[i] = p[i-1]*P;}while(m--){int l1,l2,r1,r2;cin>>l1>>r1>>l2>>r2;if(getSeg(l1,r1) == getSeg(l2,r2)) cout<<"Yes"<<endl;else cout<<"No"<<endl;}return 0;
}