一、逻辑回归模型是为了解决什么问题？

        逻辑回归（Logistic Regression）是一种广义线性回归分析模型，尤其适用于解决二分类问题（输出为两个类别）。

（1）二分类举例

• 邮件过滤：判断一封电子邮件是否为垃圾邮件。结果为垃圾邮件（1）或非垃圾邮件（0）；
• 医疗诊断：判断病人是否患有某种疾病，如癌症。结果为患病（1）或健康（0）；
• 情感分析：针对一段文本评论，判断其情感倾向是积极（1）还是消极（0）；
• 用户点击预测：在广告推荐系统中，预测用户是否会点击展示的广告。结果为点击（1）或未点击（0）

        逻辑回归虽然最初是设计来处理二分类问题的，它其实是回归模型的一种，只不过它解决的是分类问题而不是预测问题。虽然后面他也可以使用“一对多”（One-vs-All）的策略来处理可以处理多分类问题，但我在这篇文章中只介绍逻辑回归模型处理二分类问题。

二、逻辑回归模型与sigmoid函数的关系

（1）首先我有一个线性函数

模型的核心部分是一个线性函数，即输入特征与模型参数（权重和偏置）的线性组合。

        

        

        第一个式子是我们之前学过的多元线性回归模型，第二个式子中我用一个中间变量z来接收这个多项式。其中，是线性组合的输出，是特征变量，是对应的特征权重，b是偏置项。

（2）其次我将线性函数与sigmoid函数结合

        为了将线性函数的输出转换为预测类别（通常是0或1）的概率，逻辑回归引入了sigmoid函数，它又叫做logistic函数。结合操作就是指将上面的z带入中。

其图像如下图：

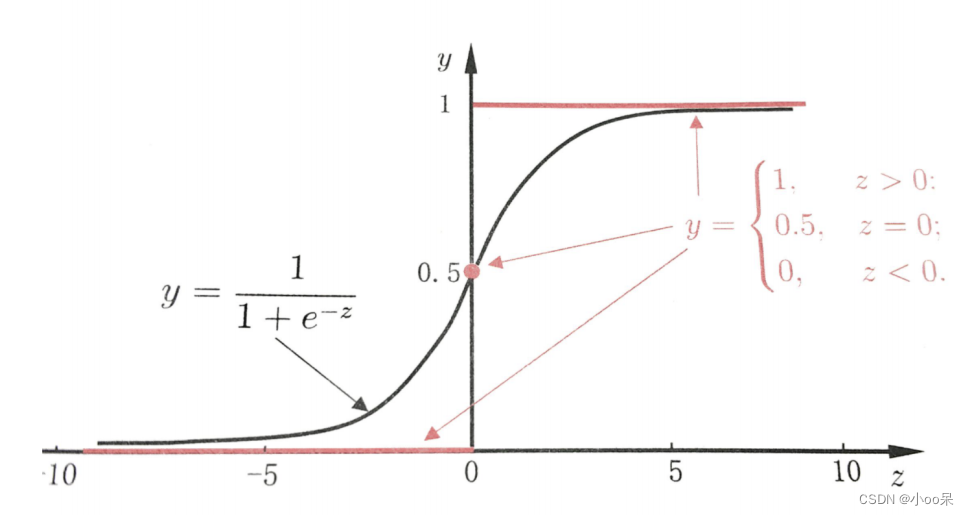
        在逻辑回归模型中，Sigmoid函数用于将样本特征的线性组合转换为概率，这个转换过程实际上是一种“概率编码”。sigmoid函数将线性函数的输出压缩并平滑地映射到(0,1)区间内，从而可以解释为正类（例如1）的概率。当预测概率大于某预定阈值（通常取0.5）时，模型预测为正类；否则预测为负类。

（3）结合后的逻辑回归模型

逻辑回归模型的输出是这样的形式：

• x 是输入特征向量，
• θ=(w,b) 是模型参数，其中w 是权重向量，b 是偏置项，
• σ 是sigmoid函数，
• P(y=1∣x;θ) 表示给定特征 x 的条件下，样本属于正类的概率。