2023年算法CDO-CNN-BiLSTM-ATTENTION回归预测（matlab）

CDO-CNN-BiLSTM-Attention切诺贝利灾难优化器优化卷积-长短期记忆神经网络结合注意力机制的数据回归预测 Matlab语言。

切诺贝利灾难优化器Chernobyl Disaster Optimizer (CDO)是H. Shehadeh于2023年提出的新型智能优化算法，参考文献如下：

H. Shehadeh.Chernobyl Disaster Optimizer (CDO): A Novel Metaheuristic Method for Global Optimization, Neural Computing and Applications. DOI: Chernobyl disaster optimizer (CDO): a novel meta-heuristic method for global optimization | Neural Computing and Applications

该方法是受到切尔诺贝利核反应堆堆芯爆炸而来的启发。它模拟了切诺贝利核事故中的灾难性事件，并通过优化算法来寻找最优解。该算法的核心思想是通过模拟灾难事件，找到最优的应对策略，从而得到最优解。CDO算法的优化过程可以被描述为一个动态的搜索过程，它不断地调整参数和策略，以适应不断变化的环境。

CDO算法具有以下几个特点：在CDO方法中，放射性的发生是由于核的不稳定性，核爆炸会发出不同类型的辐射。这些辐射中最常见的种类被称为伽马、贝塔和阿尔法粒子。它是一种自适应的优化算法，能够根据环境的变化自动调整参数和策略。具有较强的鲁棒性，能够应对各种复杂的优化问题。

代码介绍如下：

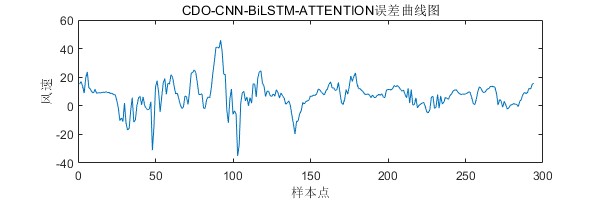
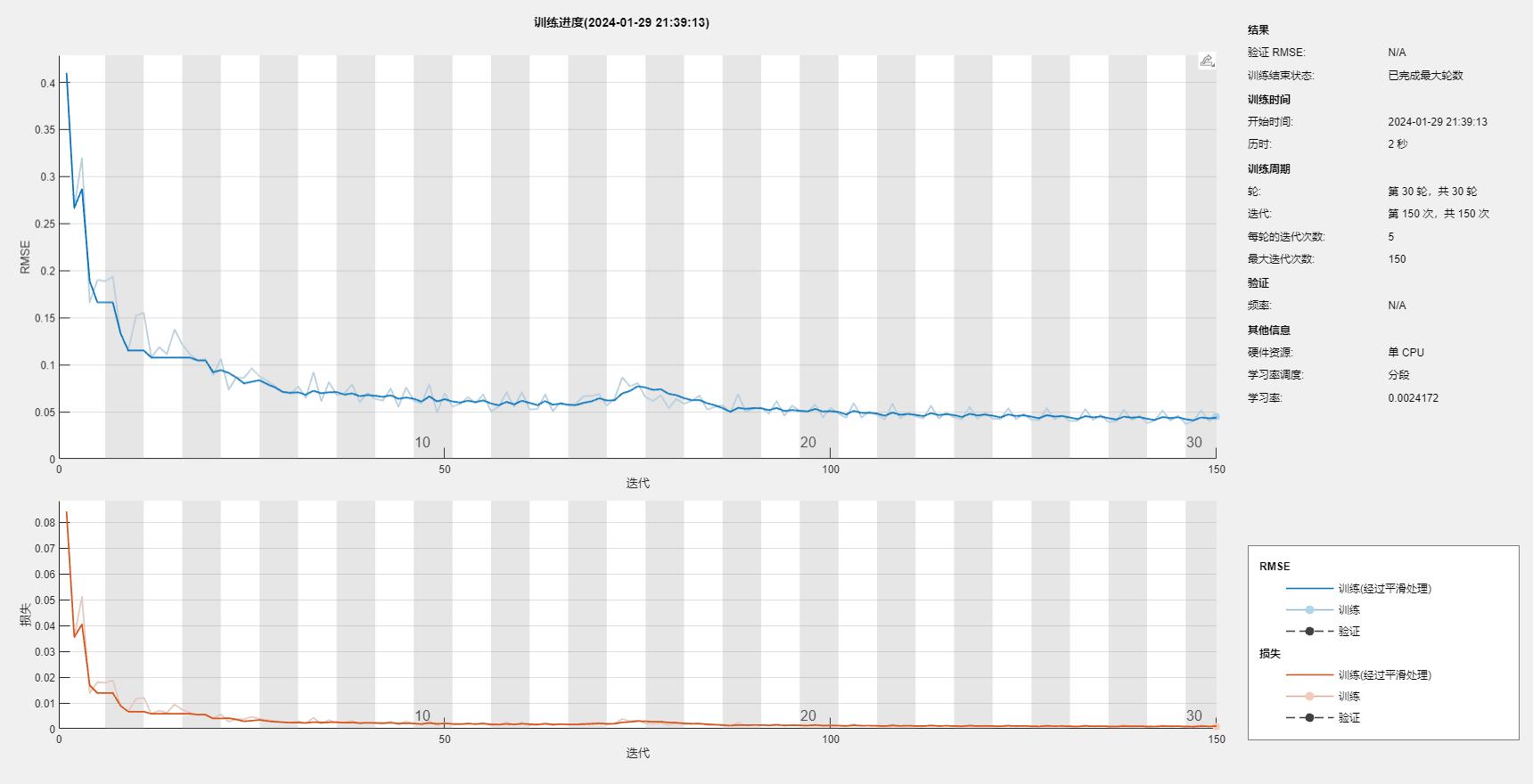
1.多变量单输出，优化的参数为：卷积核的大小，隐藏单元数目，最大训练周期，初始学习率。评价指标包括:R2、MAE、RMSE和MAPE等，图很多，出图结果如图所示，可完全满足您的需求

2.切诺贝利灾难优化器也可以替换成其他算法，比如麻雀、鹈鹕、蜣螂等等，也可定制改进～

3.直接替换Excel数据即可用，适合新手小白

4.附赠风力发电功率测试数据，可直接运行

5.商品只是提供模型，价格不包含讲解，发货后可保证运行，但程序类商品不支持退换

6.由于每个人的数据集都是独一无二的，因此预测效果不同，无法保证替换数据就一定得到您满意的结果～

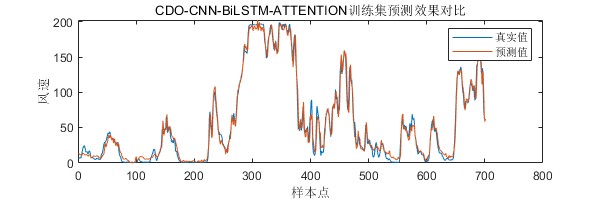
实验结果如下：

部分代码如下：

clc;clear; close all
% CDO_CNN_BiLSTM_ATTENTION预测
X = xlsread('风电场预测.xlsx');
X = X(5665:6665,:);  %选取部分数据
disp('…………………………………………………………………………………………………………………………')
disp('CDO_CNN_BiLSTM_ATTENTION预测')
disp('由于数据量大，程序运行较慢，请耐心等待！')
disp('…………………………………………………………………………………………………………………………')
% CDO参数设置
pop=5; % 种群数量
Max_iter=10; % 最大迭代次数 
dim=4; % 优化4个超参数参数 卷积核的大小 隐藏单元数目 最大训练周期 初始学习率
lb = [32, 15,30,0.001];%下边界
ub = [128,150,500,0.1];%上边界
fobj = @(x) fun(x,X) ;
[Best_score,Best_pos,curve]=CDO(pop,Max_iter,lb,ub,dim,fobj);
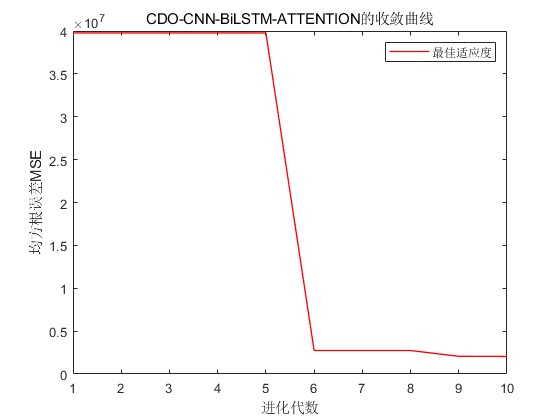
% 绘制进化曲线
figure
plot(curve,'r-','linewidth',1)
xlabel('进化代数')
ylabel('均方根误差MSE')
legend('最佳适应度')
title('CDO-CNN-BiLSTM-ATTENTION的收敛曲线')
disp('')
disp(['卷积核的大小为   ',num2str(round(Best_pos(1)))]);
disp(['最优隐藏单元数目为   ',num2str(round(Best_pos(2)))]);
disp(['最优最大训练周期为   ',num2str(round(Best_pos(3)))]);
disp(['最优初始学习率为   ',num2str((Best_pos(4)))]);
%%  将最佳参数回带
num_samples = length(X);       % 样本个数 
kim = 6;                      % 延时步长（kim个历史数据作为自变量）
zim =  1;                      % 跨zim个时间点进行预测
or_dim = size(X,2);
%  重构数据集
for i = 1: num_samples - kim - zim + 1res(i, :) = [reshape(X(i: i + kim - 1,:), 1, kim*or_dim), X(i + kim + zim - 1,:)];
end