快速排序是Hoare于1962年提出的一种二叉树结构的交换排序算法,其基本思想是:任取待排序序列中的某元素作为基准值,按照该基准值将待排序集合分割成两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列递归该过程,直到所有元素都排列在相应的位置上为止。
- 排序对象:数组、链表
- 时间复杂度:
- 空间复杂度:
- 是否稳定:否
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}上述为快速排序算法递归实现的主框架,与二叉树前序遍历的规则类似。
快速排序算法可以由多种实现方法,如霍尔法、挖坑法、前后指针法,目前最优的算法是前后指针法,其基本思路是:
- 选择数组中的一个元素作为枢轴(一般是第一个元素),其元素为关键值key,而key值最好是数组的中位数(仅在前中后三个元素中取中位数)
- 将数组划分为两个子数组,左子数组的元素都小于等于枢轴元素,右子数组的元素都大于等于枢轴元素
- 对这两个子数组分别递归调用快速排序算法,继续进行划分和排序
- 递归的结束条件是子数组的长度为1或0,即已经有序或为空数组,不需要再进行排序
- 通过不断划分和排序,最终实现整体的排序
- 在划分过程中,通过比价元素与枢轴元素的大小关系,将元素划分到对应的区域
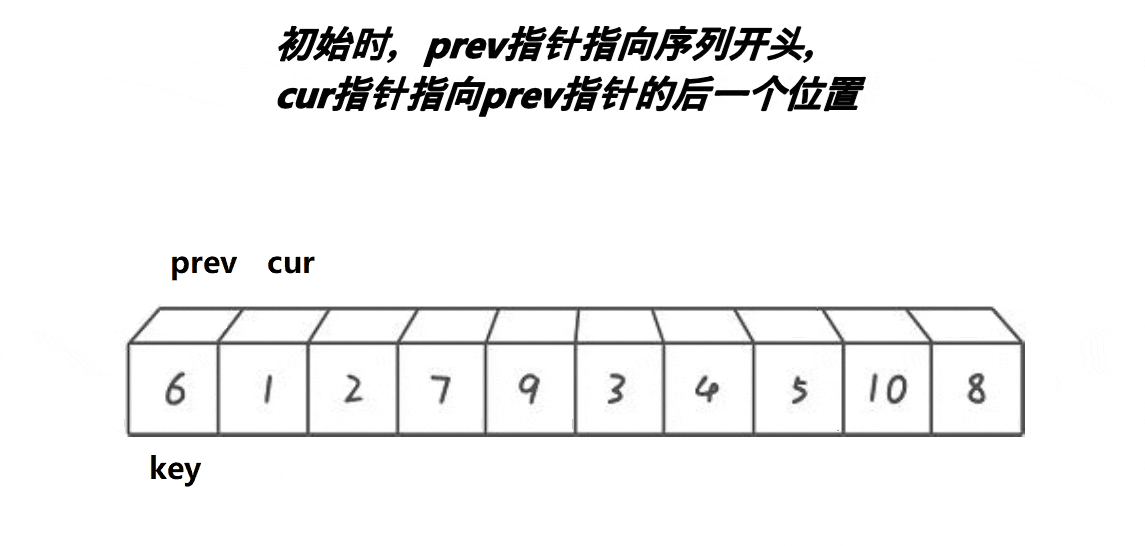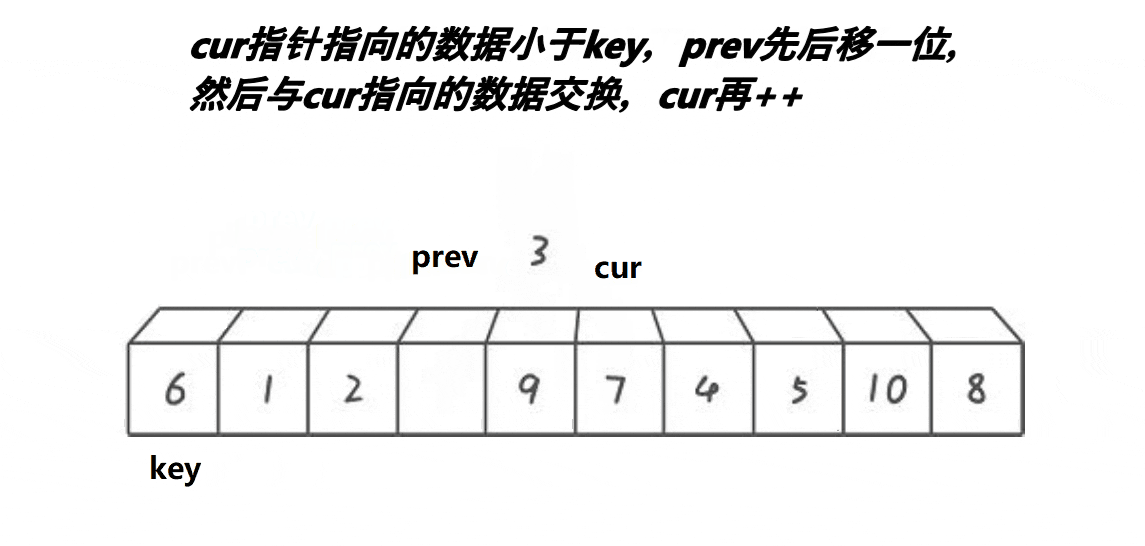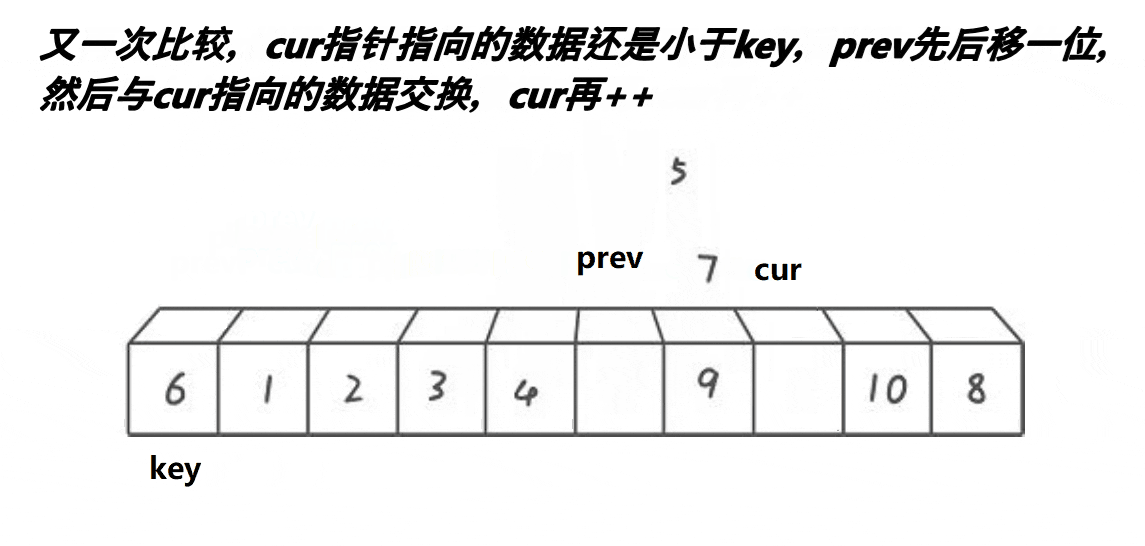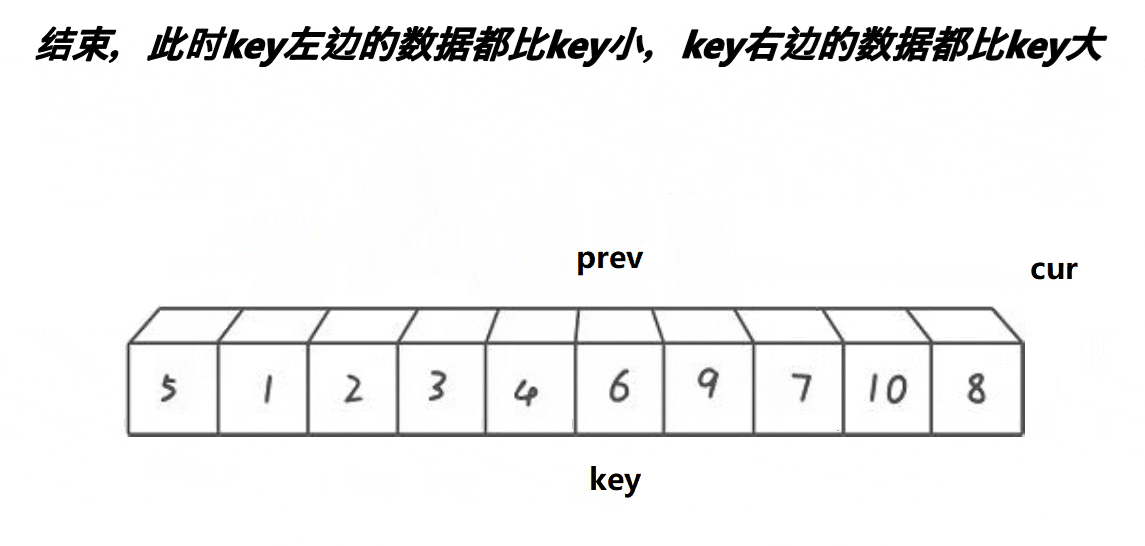
// 数组开始、中间、结尾三个元素找到中位数,将其作为key值并返回下标
int MidIndex(int* arr, int l, int m, int r)
{if (arr[l] < arr[r]){if (arr[m] < arr[l])return l;else if (arr[m] > arr[r])return r;elsereturn m;}else{if (arr[m] > arr[l])return l;else if (arr[m] < arr[r])return r;elsereturn m;}
}// 前后指针法(快慢指针法)
// 快排每一次递归的核心就是PtrPtr算法返回新的关键字key的下标
// 每一次PtrPtr算法就是为了将小于key的数移到key的左边,将大于key的数移到key的右边
// 当多次进行递归后,数组的有序度已经很高了,所以此时也可以不再递归而是采用直接插入排序
int PtrPtr(int* arr, int begin, int end)
{if (begin >= end)return;int slow = begin;int fast = slow + 1;while (fast <= end){if (arr[fast] < arr[begin] && ++slow != fast)Swap(&arr[slow], &arr[fast]);fast++;}Swap(&arr[begin], &arr[slow]);return slow; // 返回新的key值下标
}void QuickSort(int* arr, int begin, int end)
{if (begin >= end)return;int mid = (begin + end) / 2;int iKey = MidIndex(arr, begin, mid, end);Swap(&arr[begin], &arr[iKey]);iKey = PtrPtr(arr, begin, end);QuickSort(arr, begin, iKey - 1);QuickSort(arr, iKey + 1, end);
}