数据结构和算法笔记5：堆和优先队列

今天来讲一下堆，在网上看到一个很好的文章，不过它实现堆是用Golang写的，我这里打算用C++实现一下：

Golang: Heap data structure

1. 基本概念

满二叉树（二叉树每层节点都是满的）：

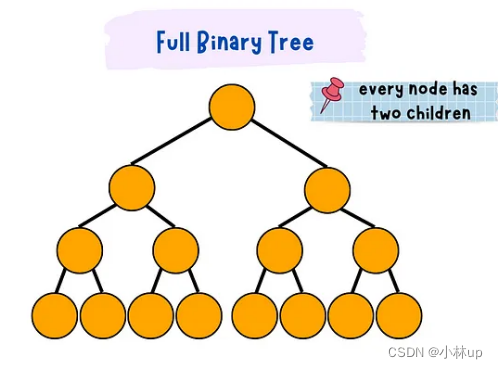
在这里插入图片描述

完全二叉树：叶子节点只出现在最后一层或倒数第二层，并且节点都是向左聚拢
非完全二叉树：下面的二叉树不满足完全二叉树的节点都向左聚拢，所以是非完全二叉树

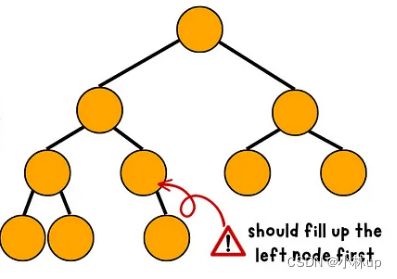
在这里插入图片描述

堆也是一颗完全二叉树。

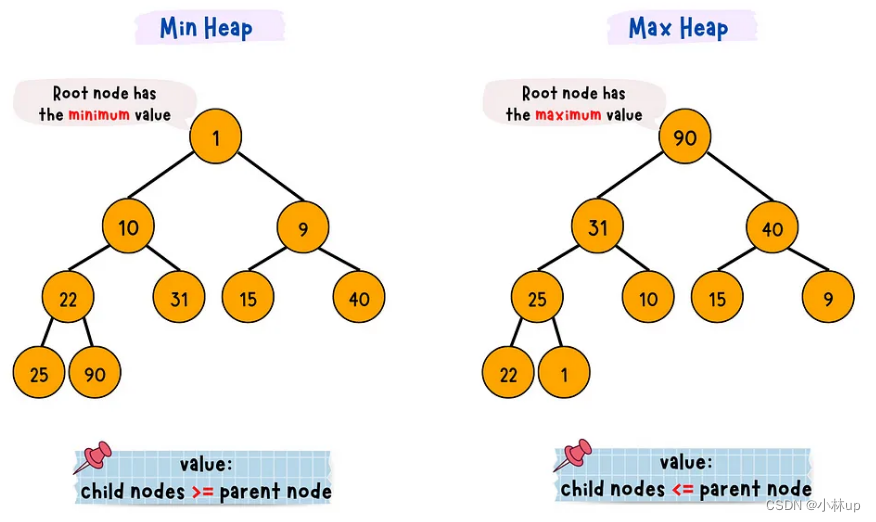
小顶堆：根节点是最小值，并且子节点大于等于父节点
大顶堆：根节点是最大值，并且子节点小于等于父节点

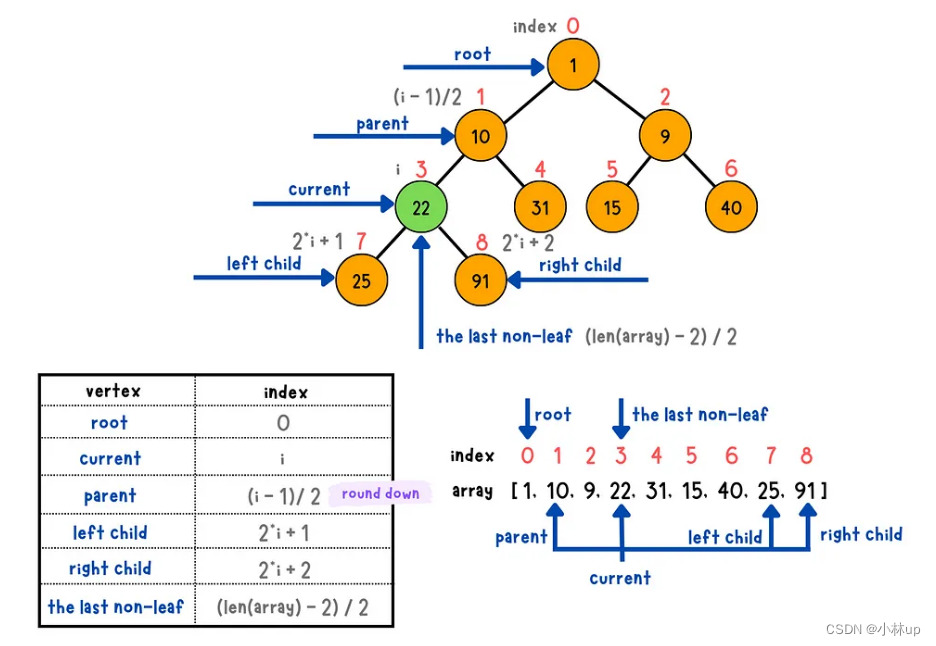
由于树的特性，堆可以用数组索引的形式表示，以小顶堆为例，在下面的小顶堆里，依次从上到下从左往右给节点编号，根节点的编号是0,：

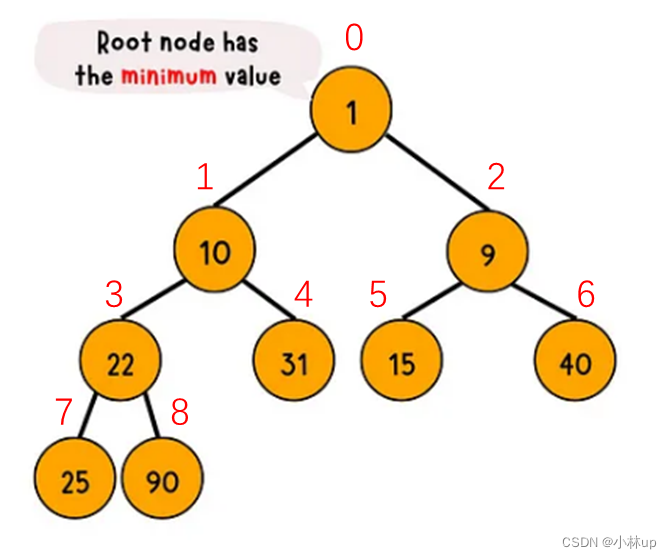
在这里插入图片描述

对应的数组为：

在这里插入图片描述
对比数组和堆，堆的索引有以下的性质：

根节点索引是0
若当前节点索引为i，如果它有父节点，父节点的索引是(i-1)/2（C++向下取整）
若当前节点索引为i，如果它有左节点，左节点的索引是2*i+1，如果它有右节点，右节点的索引是2*i+2
设数组的长度为len，最后一个非叶子节点的索引是(len-2)/2，比如上面的K是9，最后一个非叶子节点的索引是(9-2)/2=3

2. 堆的基本操作

C++有heapn内置函数来实现，具体看c++重拾 STL之heap（堆）。这里我们讲解原理，下面以小顶堆为例描述堆的相关操作

2.0 交换节点操作

我们先定义交换节点的操作，为后面调整为堆做准备：

void HeapSwap(vector<int> &minHeap, int curIndex, int swapIndex)
{int t = minHeap[curIndex];minHeap[curIndex] = minHeap[swapIndex];minHeap[swapIndex] = t;
}

2.1 下浮操作

下浮操作是通过下浮的方式把一个完全二叉树调整为堆，具体的步骤是将它与它的左儿子，右儿子比较大小，如果不满足小顶堆的性质（当前节点的值大于等于左右孩子的节点的值），当前节点需要与左右孩子的最小值节点交换位置（否则不满足堆的性质），递归的完成这个过程。（时间复杂度是log(n)）

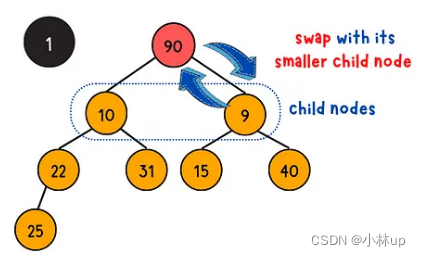
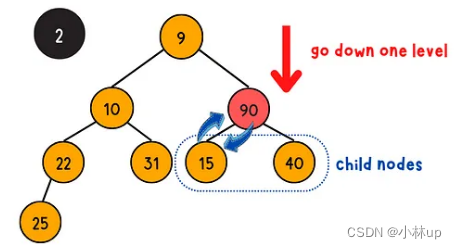
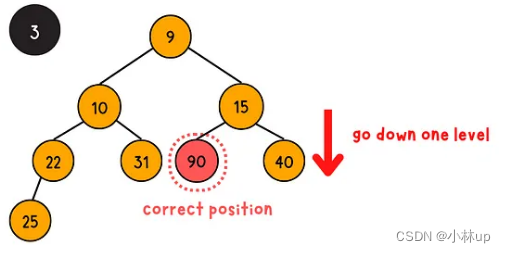
在这里插入图片描述

我们定义一个swapIndex，记录需要交换调整的节点索引，如果需要调整，这个索引是当前节点和左右子节点索引的最小值，这个过程要注意判断边界条件：

void HeapSiftDown(vector<int> &minHeap, int curIndex)
{int leftChildIndex = 2 * curIndex + 1;  // 左孩子节点的索引int rightChildIndex = 2 * curIndex + 2; // 右孩子节点的索引int swapIndex = curIndex;               // 定义调整的节点索引// 判断左右孩子是否小于当前元素，如果是把swapIndex赋值为孩子索引if (leftChildIndex < minHeap.size() && minHeap[leftChildIndex] < minHeap[swapIndex])swapIndex = leftChildIndex;if (rightChildIndex < minHeap.size() && minHeap[rightChildIndex] < minHeap[swapIndex])swapIndex = rightChildIndex;// 判断交换索引和当前索引是不是一样，如果不一样说明要交换，然后继续SiftDown，直到到最后一个节点if (curIndex != swapIndex){HeapSwap(minHeap, curIndex, swapIndex);HeapSiftDown(minHeap, swapIndex);}
}

2.2 上浮操作

上浮操作是通过上浮的方式把一个完全二叉树调整为堆，具体的步骤是将它与它的父亲节点比较大小，如果不满足小顶堆的性质（父亲的节点的值大于等于当前节点的值），当前节点与父亲节点交换位置（否则不满足堆的性质），递归的完成这个过程。（时间复杂度是log(n)）

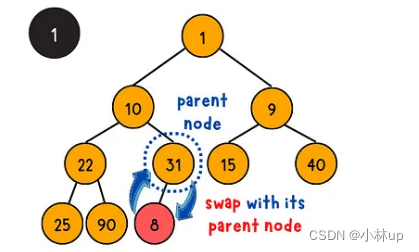
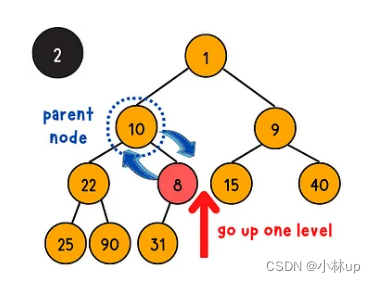
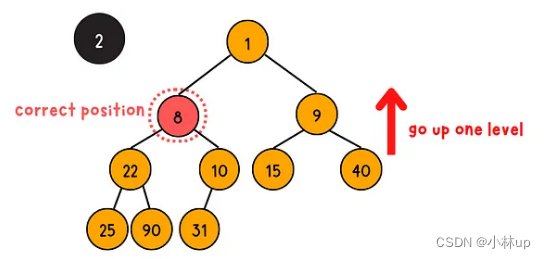
在这里插入图片描述

在这里插入图片描述

我们类似上浮操作定义一个swapIndex，记录需要交换调整的节点索引，如果需要调整，这个索引是父亲节点的索引，这个过程要注意判断边界条件：

void HeapSiftUp(vector<int> &minHeap, int curIndex)
{int parentIndex = (curIndex - 1) / 2;//父亲节点的索引int swapIndex = curIndex;// 定义调整的节点索引// 判断左右孩子是否小于当前元素，如果是把swapIndex赋值为孩子索引if (parentIndex >= 0 && minHeap[curIndex] < minHeap[parentIndex])swapIndex = parentIndex;// 判断交换索引和当前索引是不是一样，如果不一样说明要交换，然后继续SiftUp，直到到最后一个节点if (curIndex != swapIndex){HeapSwap(minHeap, curIndex, swapIndex);HeapSiftUp(minHeap, swapIndex);}
}

2.3 给定一个数组建堆

建堆有上浮和下浮两种方法：

如果是下浮的方法，可以直接从最后一个不是叶节点的节点开始往上下浮（叶子节点没有左右孩子一定不需要交换）。这里使用了前面堆索引性质的第四条：

设数组的长度为len，最后一个非叶子节点的索引是(len-2)/2

void HeapBuild(vector<int> &array)
{int lastNoLeafIndex = (array.size() - 2) / 2;for (int i = lastNoLeafIndex; i >= 0; i--)//从最后一个不是叶节点的节点开始往上下浮HeapSiftDown(array, i);
}

如果是上浮的方法，则从索引为1节点开始往下上浮（根节点没有父亲节点一定不需要交换）。

void HeapBuild(vector<int> &array)
{for (int i = 1; i < array.size(); ++i)//从索引为1节点开始往下上浮HeapSiftUp(array, i);
}

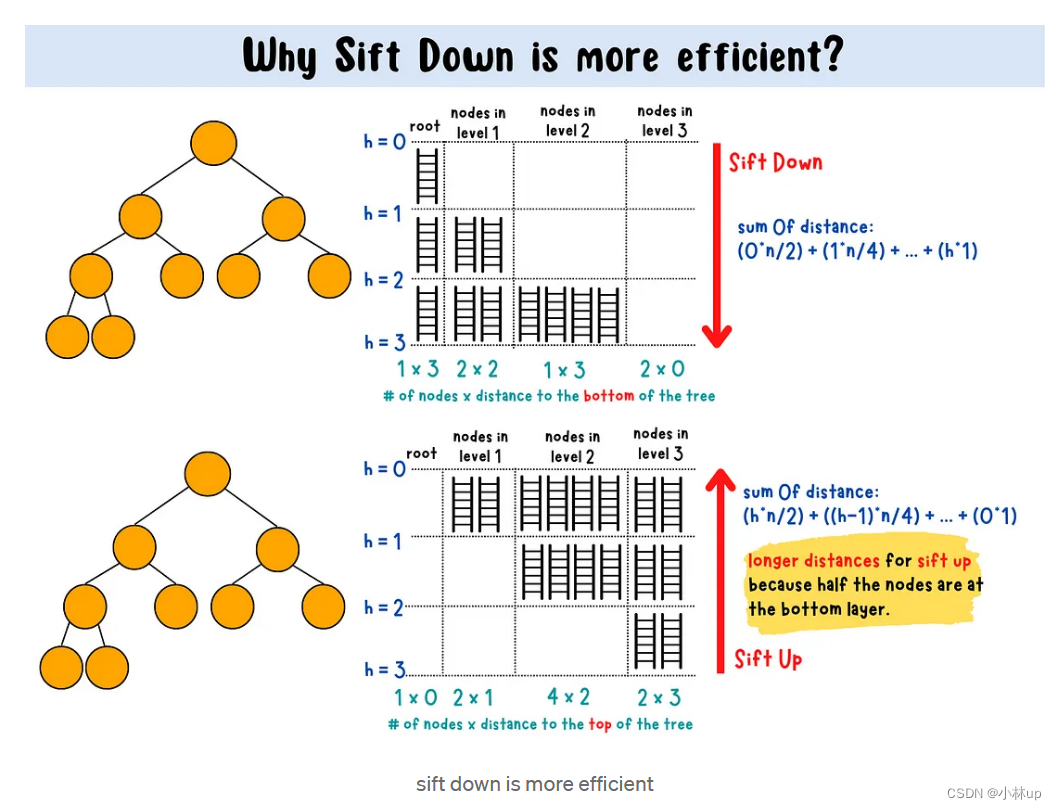
使用下浮建堆的时间复杂度是O(n)，而使用上浮建堆的时间复杂度是O(nlogn)，建议使用下浮建堆。关于复杂度参考How can building a heap be O(n) time complexity?
在这里插入图片描述

2.4 Pop操作

pop操作是把根节点弹出返回，并重新调整剩余元素构成的数组为堆，数组的长度为len，这里我们把根节点和最后一个节点交换，中间要保留根节点的值，然后把数组调整为len-1（因为弹出一个元素了），重新用下浮调整为堆，然后返回堆的根节点的值。时间复杂度是log(n)

int HeapPop(vector<int> &minHeap)
{int value = minHeap[0];//保留堆的根节点的值int len = minHeap.size();//记录堆的大小HeapSwap(minHeap, 0, len - 1);//把堆的根节点和最后一个节点交换minHeap.resize(len - 1);//调整数组长度为len-1HeapSiftDown(minHeap, 0);//下浮调整为堆return value;//返回堆的根节点的值
}

2.5 Push操作

push操作是在数组末尾加入元素num，然后重新调整成堆。相比pop操作，push操作就简单很多了，我们先在数组末尾加入元素num，然后从最后一个元素的索引开始使用上浮即可。时间复杂度是log(n)

void HeapPush(vector<int> &minHeap, int num)
{minHeap.push_back(num);//在数组末尾加入元素numHeapSiftUp(minHeap, minHeap.size() - 1);//从最后一个元素的索引开始使用上浮
}

测试：

完整代码：

#include <iostream>
#include <vector>
using namespace std;void HeapSiftDown(vector<int> &minHeap, int curIndex);
void HeapSiftUp(vector<int> &minHeap, int curIndex);
void HeapSwap(vector<int> &minHeap, int curIndex, int swapIndex);
void HeapBuild(vector<int> &array);
void HeapPush(vector<int> &minHeap, int num);void HeapBuild(vector<int> &array)
{int lastNoLeafIndex = (array.size() - 2) / 2;for (int i = lastNoLeafIndex; i >= 0; i--)HeapSiftDown(array, i);
}void HeapSiftDown(vector<int> &minHeap, int curIndex)
{int leftChildIndex = 2 * curIndex + 1; int rightChildIndex = 2 * curIndex + 2;int swapIndex = curIndex;               if (leftChildIndex < minHeap.size() && minHeap[leftChildIndex] < minHeap[swapIndex])swapIndex = leftChildIndex;if (rightChildIndex < minHeap.size() && minHeap[rightChildIndex] < minHeap[swapIndex])swapIndex = rightChildIndex;if (curIndex != swapIndex){HeapSwap(minHeap, curIndex, swapIndex);HeapSiftDown(minHeap, swapIndex);}
}void HeapSiftUp(vector<int> &minHeap, int curIndex)
{int parentIndex = (curIndex - 1) / 2;int swapIndex = curIndex;if (parentIndex >= 0 && minHeap[curIndex] < minHeap[parentIndex])swapIndex = parentIndex;if (curIndex != swapIndex){HeapSwap(minHeap, curIndex, swapIndex);HeapSiftUp(minHeap, swapIndex);}
}
void HeapSwap(vector<int> &minHeap, int curIndex, int swapIndex)
{int t = minHeap[curIndex];minHeap[curIndex] = minHeap[swapIndex];minHeap[swapIndex] = t;
}int HeapPop(vector<int> &minHeap)
{int value = minHeap[0];int len = minHeap.size();HeapSwap(minHeap, 0, len - 1);minHeap.resize(len - 1);HeapSiftDown(minHeap, 0);return value;
}void HeapPush(vector<int> &minHeap, int num)
{minHeap.push_back(num);HeapSiftUp(minHeap, minHeap.size() - 1);
}int main()
{vector<int> array{9, 31, 40, 22, 10, 15, 1, 25, 91};cout << "The origin array is " << endl;for (auto &t : array)cout << t << " ";cout << endl<< "---------------------------------------------------" << endl;// 建堆HeapBuild(array);cout << "After build the heap, the array is " << endl;for (auto &t : array)cout << t << " ";cout << endl<< "---------------------------------------------------" << endl;// pop元素int top = HeapPop(array);cout << "The pop value is " << top << endl;cout << "After pop, the array is " << endl;for (auto &t : array)cout << t << " ";cout << endl<< "---------------------------------------------------" << endl;// push元素HeapPush(array, 1);cout << "After push, the array is " << endl;for (auto &t : array)cout << t << " ";cout << endl<< "---------------------------------------------------" << endl;
}

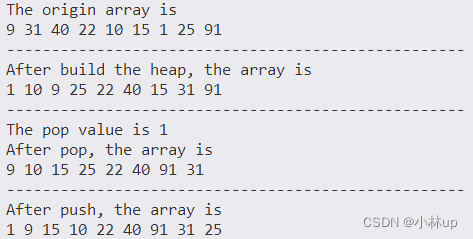
在这里插入图片描述

可以自行印证上面满足小顶堆。大顶堆的思路和小顶堆的思路差不多。读者可以自己实现一下。

3. 堆的相关使用

3.1 堆排序

堆排序基本的思路是：

初始化：数组建堆
数组的根节点和堆的最后一个节点交换
剩余元素重新排成堆（堆的长度减1），然后继续第2步操作直到数组的长度为1

这里也放一个算法导论的截图（不过它的根节点的索引是1），思路是差不多的：

在这里插入图片描述

我们这里使用小顶堆，小顶堆的根节点是最小值，每次第2步和后面的节点做交换，所以最后排序是从大到小（最小值根节点都放到数组的后面）。

前面的建堆是对整个数组来说的，但是对于堆排序，我们需要划定要排序数组的范围，所以我们对建堆和下浮两个操作另外定义一个函数：

HeapSiftDown函数

注意这里的数组越界处理改为了传入的heapLength，我们只需要对0-heapLength-1范围的数组做下浮的操作

void HeapSiftDown(vector<int> &minHeap, int curIndex, int heapLength)
{int leftChildIndex = 2 * curIndex + 1;  // 左孩子节点的索引int rightChildIndex = 2 * curIndex + 2; // 右孩子节点的索引int swapIndex = curIndex;               // 定义和当前索引交换的索引// 判断左右孩子是否小于当前元素，如果是把swapIndex换给孩子索引，注意这里的数组越界处理改为了传入的heapLength if (leftChildIndex < heapLength && minHeap[leftChildIndex] < minHeap[swapIndex])swapIndex = leftChildIndex;if (rightChildIndex < heapLength && minHeap[rightChildIndex] < minHeap[swapIndex])swapIndex = rightChildIndex;// 判断交换索引和当前索引是不是一样，如果不一样说明要交换，继续SiftDown，直到到最后一个节点if (curIndex != swapIndex){HeapSwap(minHeap, curIndex, swapIndex);HeapSiftDown(minHeap, swapIndex, heapLength);}
}

HeapBuild函数

注意这里的计算最后一个非叶子节点的索引使用了传入的heapLength，相当于对0-heapLength-1范围的数组建堆

void HeapBuild(vector<int> &array, int heapLength)
{int lastNoLeafIndex = (heapLength - 2) / 2;//注意这里最后一个非叶子节点的索引使用的是传入的heapLengthfor (int i = lastNoLeafIndex; i >= 0; i--)HeapSiftDown(array, i, heapLength);
}

OK我们可以写堆排序了，传入一个数组：

void HeapSort(vector<int> &array)
{int heapLength = array.size();//建堆的长度int len = array.size();//数组的长度HeapBuild(array, heapLength);for (int i = len - 1; i >= 1; --i)//遍历到索引1就行，索引0不需要遍历，因为只有一个数了{HeapSwap(array, 0, i);//把索引0（根节点）和索引i节点交换heapLength--;//建堆的长度减1HeapBuild(array, heapLength);//再次对0~heapLength-1的数组建堆}
}

测试堆排序

#include <iostream>
#include <vector>
using namespace std;
void HeapBuild(vector<int> &array, int heapLength);
void HeapSort(vector<int> &array);void HeapBuild(vector<int> &array, int heapLength)
{int lastNoLeafIndex = (heapLength - 2) / 2;//注意这里最后一个非叶子节点的索引使用的是传入的heapLengthfor (int i = lastNoLeafIndex; i >= 0; i--)HeapSiftDown(array, i, heapLength);
}
void HeapSort(vector<int> &array)
{int heapLength = array.size();//建堆的长度int len = array.size();//数组的长度HeapBuild(array, heapLength);for (int i = len - 1; i >= 1; --i)//遍历到索引1就行，索引0不需要遍历，因为只有一个数了{HeapSwap(array, 0, i);//把索引0（根节点）和索引i节点交换heapLength--;//建堆的长度减1HeapBuild(array, heapLength);//再次对0~heapLength-1的数组建堆}
}
int main()
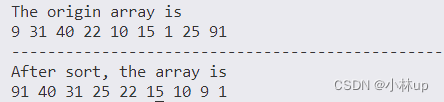
{vector<int> array{9, 31, 40, 22, 10, 15, 1, 25, 91};cout << "The origin array is " << endl;for (auto &t : array)cout << t << " ";cout << endl<< "---------------------------------------------------" << endl;// sort元素HeapSort(array);cout << "After sort, the array is " << endl;for (auto &t : array)cout << t << " ";return 0;
}

可以看到从大到小进行了排序，如果用大顶堆，就是从小到大排序。
在这里插入图片描述

3.2 优先队列

优先级队列虽然也叫队列，但是和普通的队列还是有差别的。普通队列出队顺序只取决于入队顺序，而优先级队列的出队顺序总是按照元素自身的优先级。可以理解为，优先级队列是一个排序后的队列。

堆和优先级队列非常相似，一个堆就可以看作一个优先级队列。往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素（大顶堆–最大值；小顶堆–最小值）。不过优先级我们还可以自己额外定义。C++有priority_queue来实现，具体可以看c++优先队列(priority_queue)用法详解。

所以优先队列有两个操作，分别是pop弹出和push加入，pop即弹出根节点，push即把新的元素加入优先队列，两种操作过后要保证剩余的元素构成的还是一个堆。直接使用前面所说的pop和push操作即可。

4. 典型例题

347. 前 K 个高频元素

前K个元素，先用哈希表记录元素的频率，然后可以使用小根堆，如果队列元素超过K可以弹出根节点（最小的元素），遍历完以后，队列里剩下的就是前K大的元素。

class Solution {
public:static bool cmp(pair<int, int>& a, pair<int, int>& b){return a.second > b.second;}vector<int> topKFrequent(vector<int>& nums, int k) {vector<int> ans;unordered_map<int, int> mp;for (auto& t: nums)mp[t]++;priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(&cmp)> que(cmp);for (auto it = mp.begin(); it != mp.end(); ++it){que.push(*it);if (que.size() > k)que.pop();}while (!que.empty()){ans.push_back(que.top().first);que.pop();}return ans;}
};

关于priority_queue的比较函数cmp也可以使用仿函数：

class Solution {
public:class cmp {public:bool operator() (const pair<int, int> &lhs, const pair<int, int> &rhs) {return lhs.second > rhs.second;}};vector<int> topKFrequent(vector<int>& nums, int k) {vector<int> ans;unordered_map<int, int> mp;for (auto& t: nums)mp[t]++;priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> que;for (auto it = mp.begin(); it != mp.end(); ++it){que.push(*it);if (que.size() > k)que.pop();}while (!que.empty()){ans.push_back(que.top().first);que.pop();}return ans;}
};

内置类型比如int的话cmp可以直接使用greater<int>（小根堆）和less<int>（大根堆），如果比较自定义的Node类型，可以在Node里重载<：

#include <queue>
#include <iostream>
using namespace std;
struct Node
{int x, y;bool operator<(const Node &rhs) const{return this->x > rhs.x; // 用x比较，这里是>，是小根堆}
};
int main()
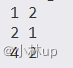
{priority_queue<Node> que;que.push(Node{1, 2});que.push(Node{2, 1});que.push(Node{4, 2});while (!que.empty()){cout << que.top().x << " " << que.top().y << endl;que.pop();}
}

215. 数组中的第K个最大元素

和上题类似，我们使用一个小顶堆，遍历完整个数组，最后剩下的根节点就是第K大元素了。

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int, vector<int>, greater<int>> que;for (auto& t:nums){que.push(t);if (que.size() > k){que.pop();}}return que.top();}
};

295. 数据流的中位数

维护一个大根堆和一个小根堆，大根堆queMin记录小于等于中位数的那些数，小根堆queMax记录大于中位数的那些数。

大根堆queMin: 大<-小
小根堆queMax：小->大

findMedian：小根堆的元素个数比大根堆的元素的个数大1或两者相等，如果是奇数直接取小根堆的根节点元素，如果是偶数取两个堆的根节点的平均值（注意返回是double，所以除以2不行，要除以2.0）

addNum：由于小根堆的元素个数比大根堆元素个数大1或两者相等，所以我们优先处理小根堆：

如果queMax的维度和queMin的维度是一样的，那么先往queMax里push num，然后queMin添加queMax的堆顶元素，queMax弹出元素。
如果queMax的维度比queMin的维度小（这时候是小1），那么先往queMin里push num，然后queMax添加queMin的堆顶元素，queMin弹出元素。

class MedianFinder {
public:MedianFinder() {}void addNum(int num) {if (queMin.size() == queMax.size()){queMax.push(num);queMin.push(queMax.top());queMax.pop();}else{queMin.push(num);queMax.push(queMin.top());queMin.pop();}}double findMedian() {if (queMin.size() > queMax.size())return queMin.top();return (queMin.top() + queMax.top()) / 2.0;}
private:priority_queue<int, vector<int>, less<int>> queMin;priority_queue<int, vector<int>, greater<int>> queMax;};/*** Your MedianFinder object will be instantiated and called as such:* MedianFinder* obj = new MedianFinder();* obj->addNum(num);* double param_2 = obj->findMedian();*/