引出

微分几何——梅向明第四版学习笔记（一） & 向量函数和曲线论

曲面论

曲面的概念

曲面的参数方程

案例：

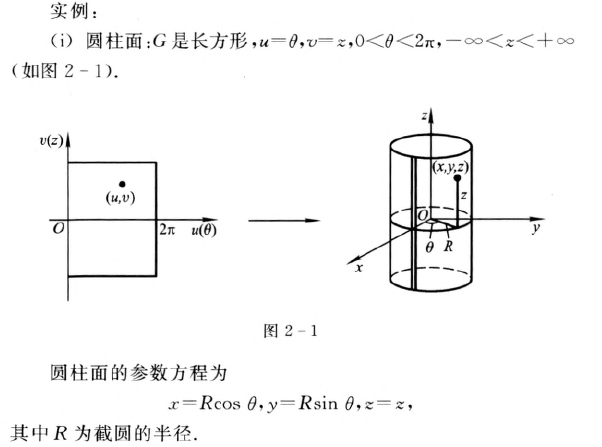
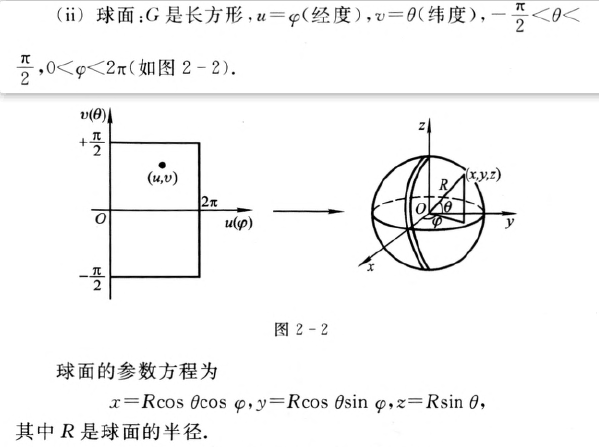
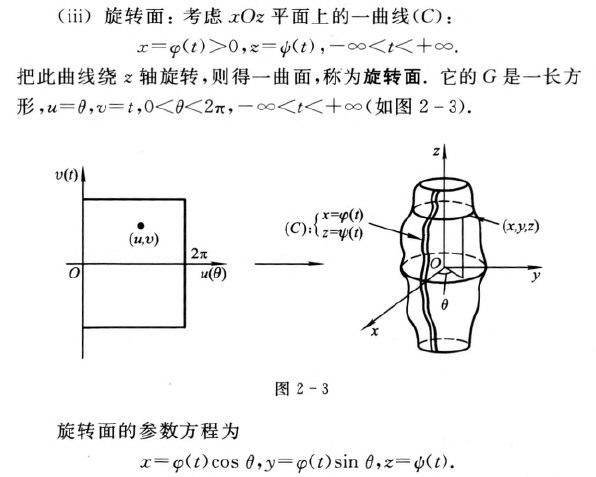
曲纹坐标网

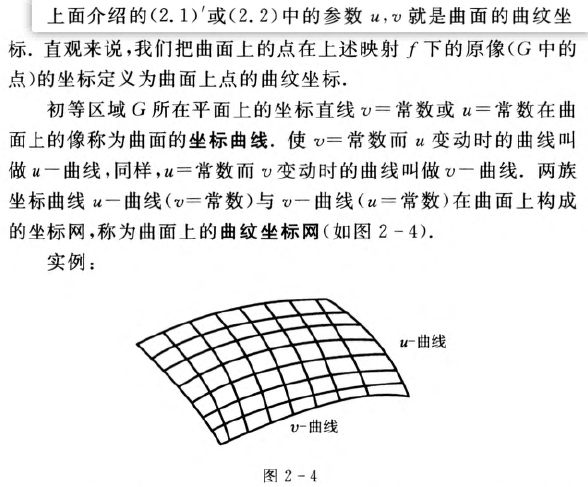
曲面的切平面和法线

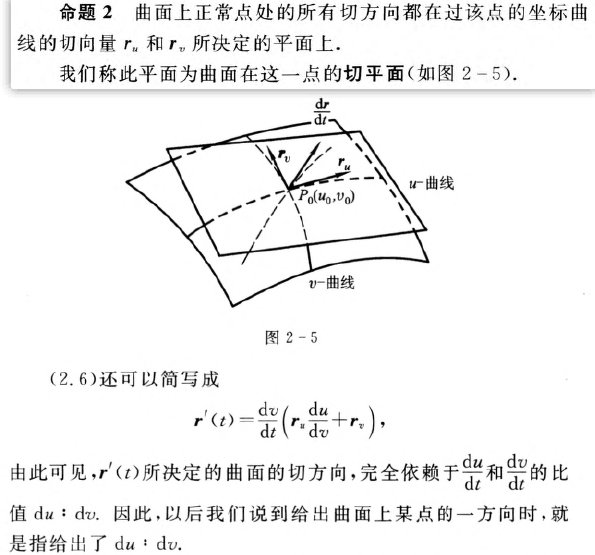
曲面某点的切平面

曲面某点的法线

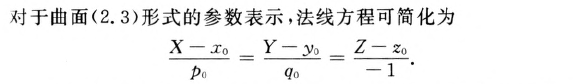
案例：

曲面的第一基本形式

案例：

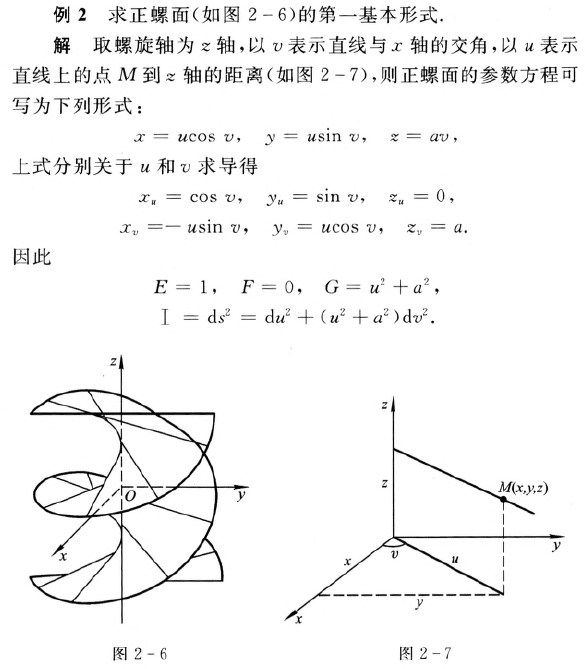
曲面域的面积

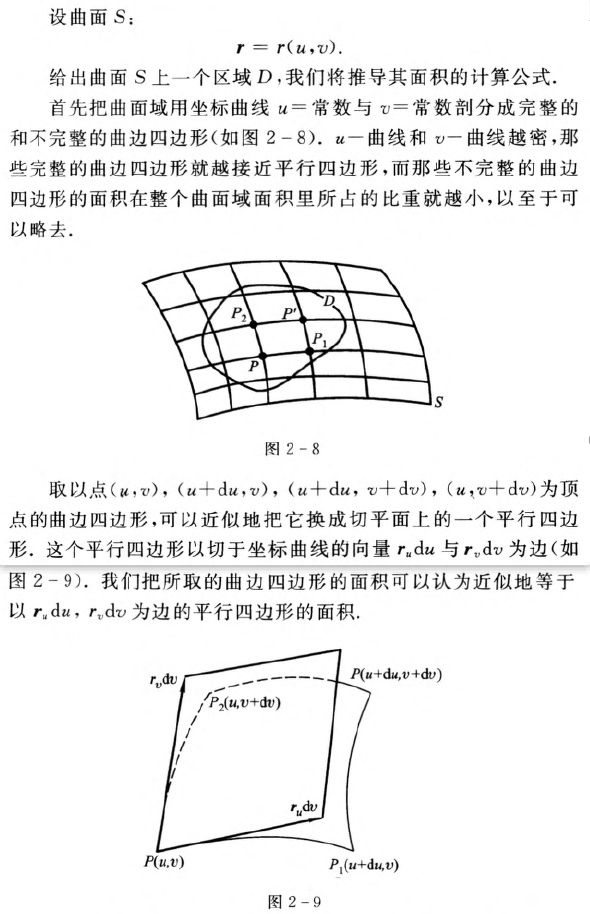
曲面的第二基本形式

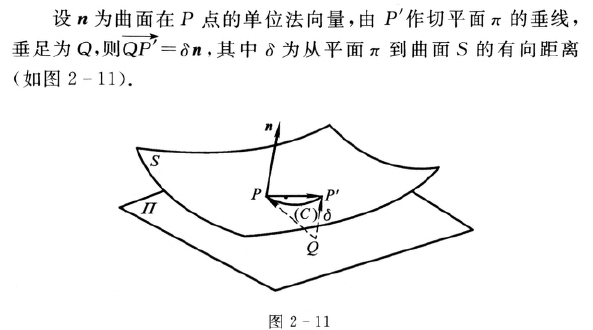
上式表明第二基本形式近似地等于曲面与切平面的有向距离的两倍，因而它刻画了曲面离开切平面的弯曲程度，即刻画了曲面在空间中的弯曲性

案例：

曲面的特殊的参数表示情形

案例：

曲面上曲线的曲率

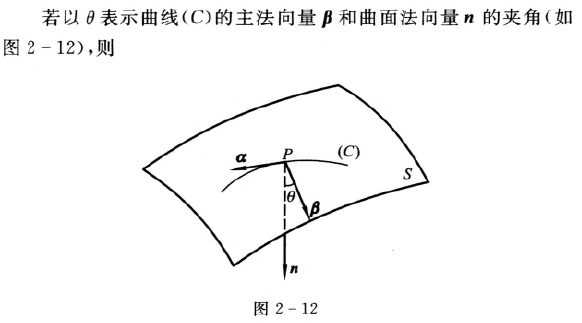
由以上的讨论我们已经了解到曲面在已知点邻近的弯曲性可以由曲面离开它的切平面的快慢来决定.但是曲面在不同的方向弯曲的程度不同，也就是说在不同的方向曲面以不同的速度离开切平面.因此，当我们想刻画曲面在已知点邻近的弯曲性时，就需要用曲面上过该点的不同的曲线的曲率来进行研究.

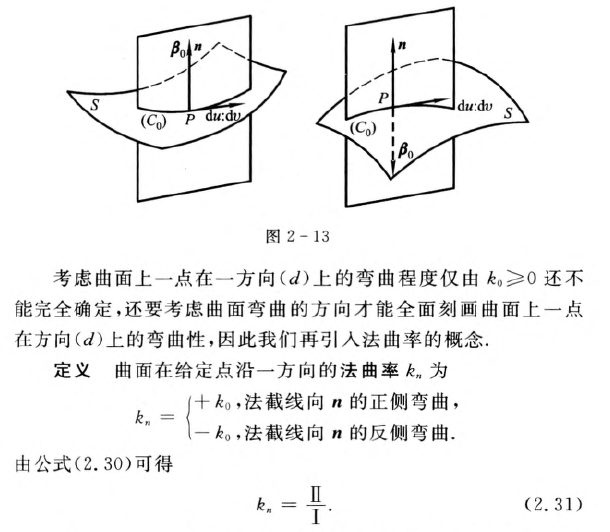
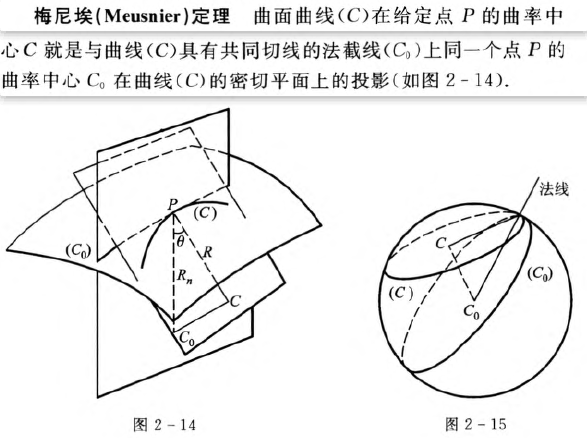
案例：

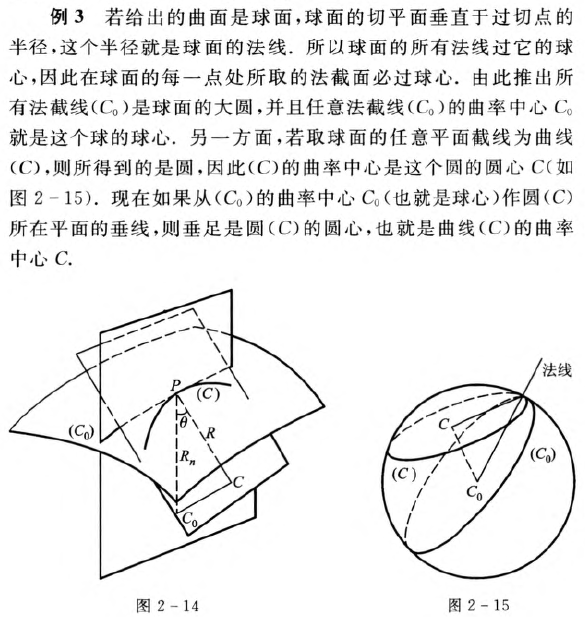
Dupin指标线

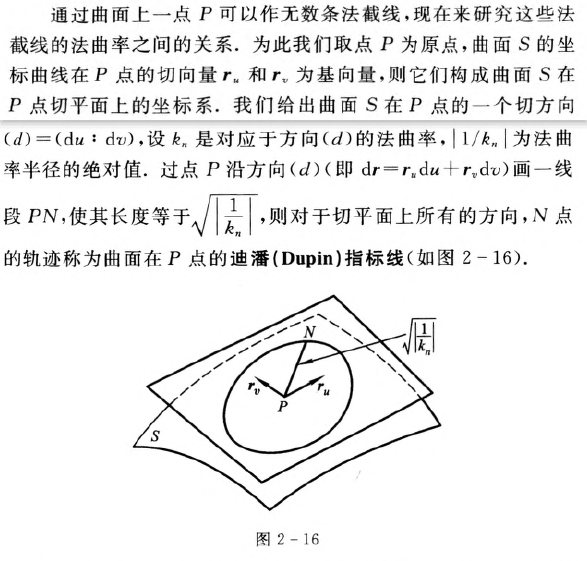
曲面的渐进方向

曲面的共轭方向

曲面的主方向和曲率线

曲面的三个曲率

主曲率

高斯曲率，平均曲率

高斯曲率和平均曲率

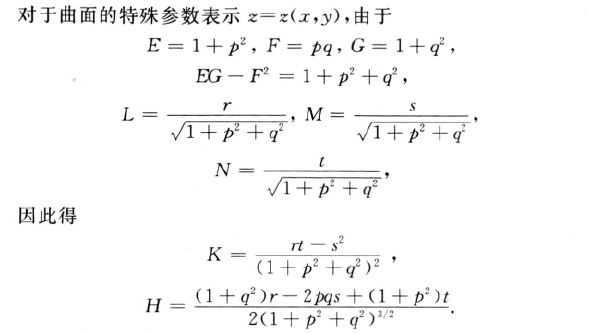
案例

曲面在一点邻近的结构

1.椭圆点：

2.双曲点：

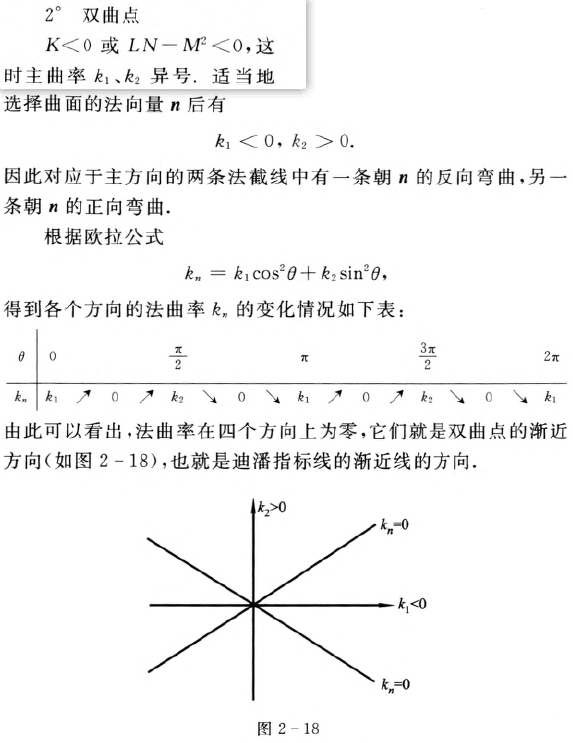
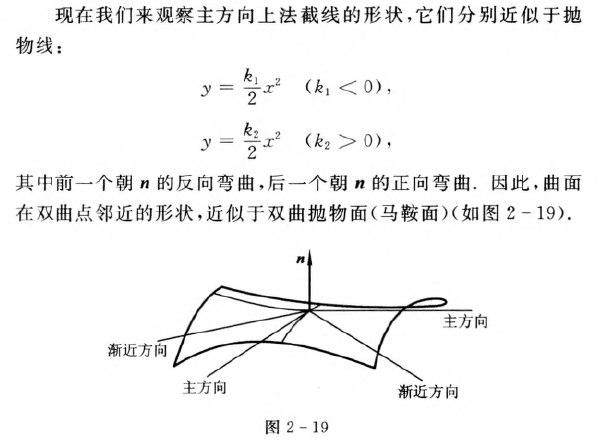
3.抛物点：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

曲面的第三基本形式

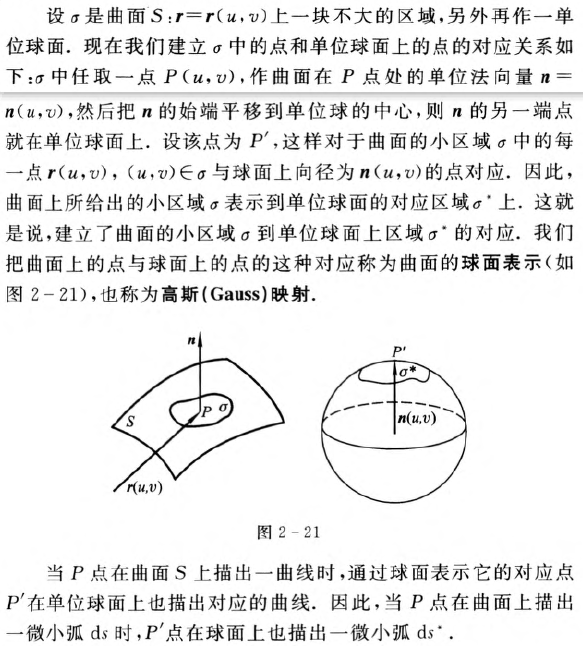
高斯曲率的几何意义

直纹面和可展曲面

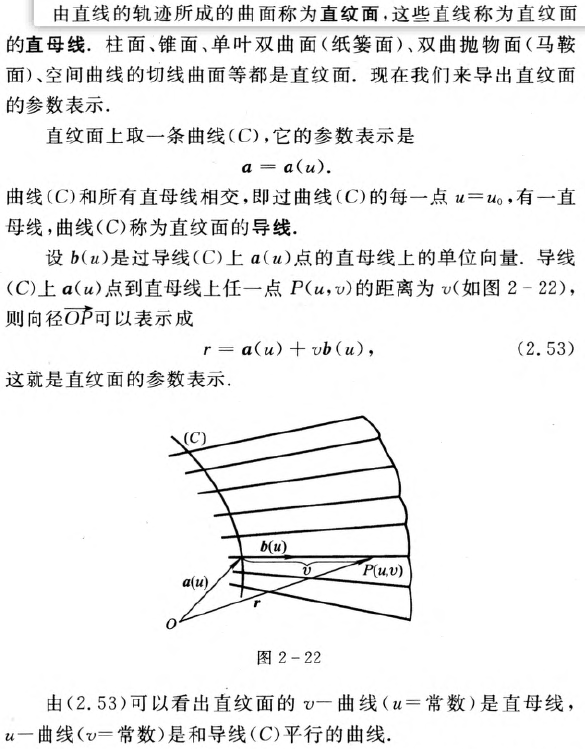
可展曲面

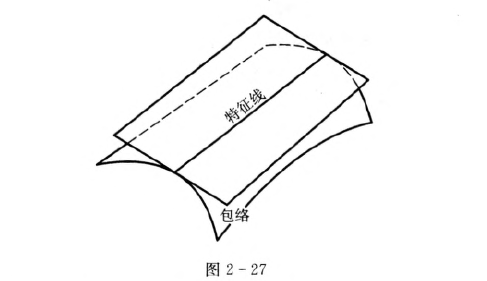
曲面论的基本定理

曲面的黎曼(Riemann)曲率张量和高斯-科达齐-迈因纳尔迪(Gauss-Codazzi-Mainardi)公式

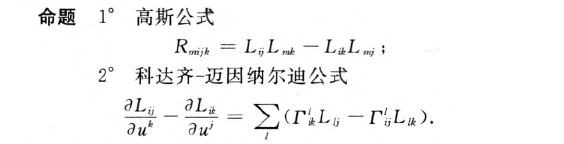
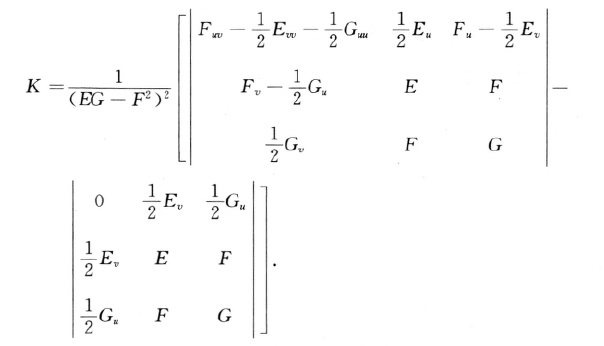
案例：

曲面论基本定理：

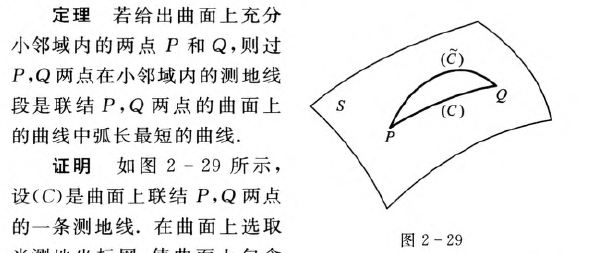
曲面上的测地线【重要】

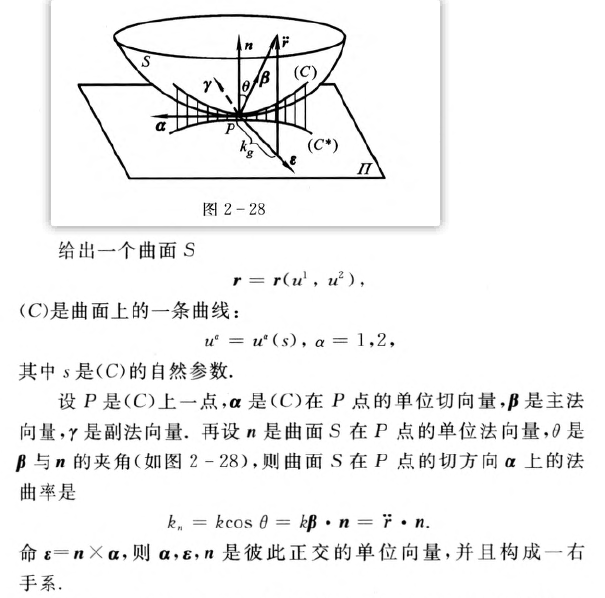
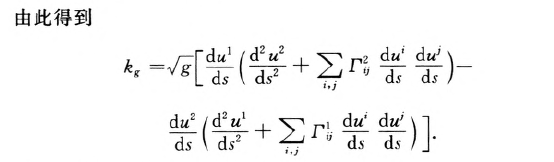
曲面上的测地线：

测地线是短程线

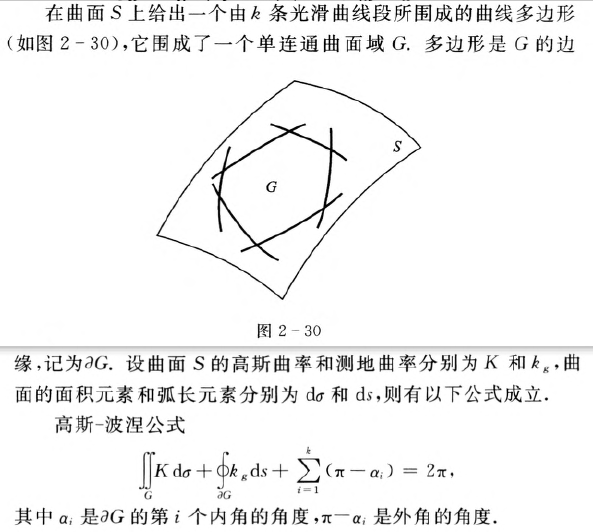
高斯波涅公式Gauss-Bonnet公式【重要】

推论：

曲面上向量的平行移动

曲面上的向量及其平行移动

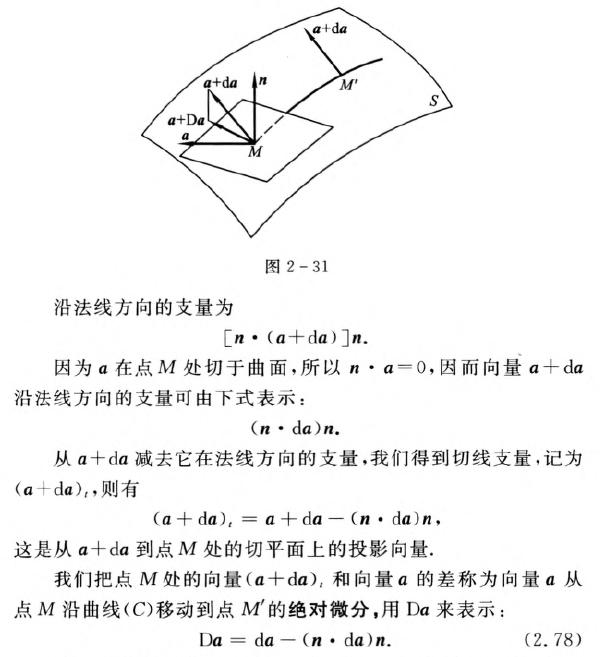
平行移动的性质

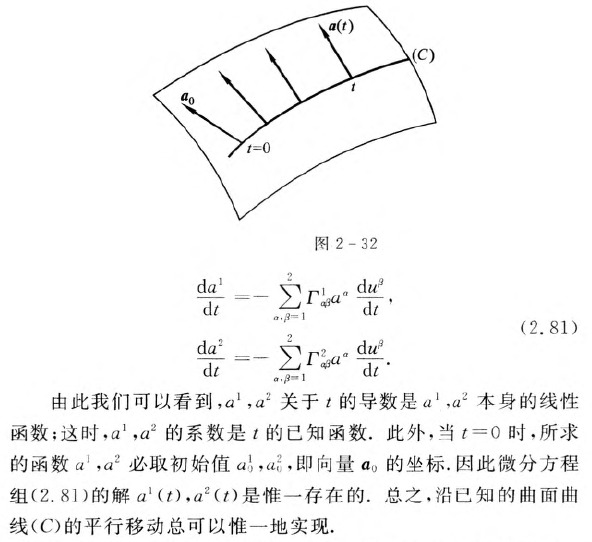
常高斯曲率的曲面

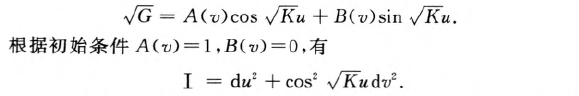
案例：

外微分形式和活动标架

格拉斯曼代数

活动标架法

活动标架法是微分几何中研究空间图形的方法，它的特点是把图形的研究安排好一定的程序，然后有步骤地去分析图形的性质

案例：

用活动标架法研究曲面

曲面的基本形式

曲面的第一基本形式：

曲面的第二基本形式

曲面的第三基本形式

曲面上的曲线，法曲率，测地曲率，测地挠率

主曲率：

平均曲率：

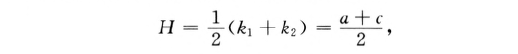
高斯曲率：

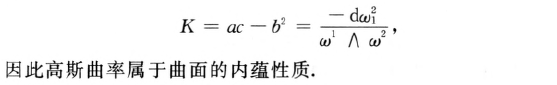
闭曲面的高斯-波涅公式【重要】

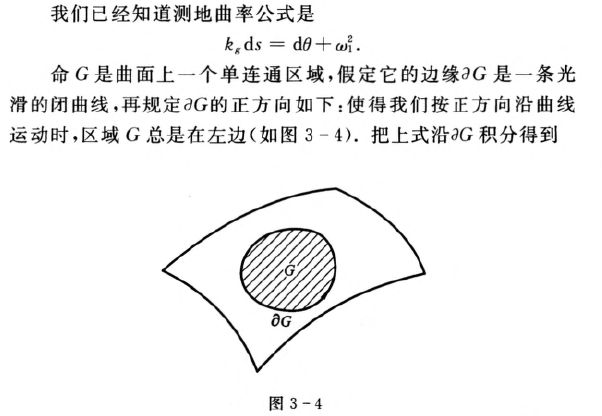
特别地，如果区域G的边缘时测地线，则Kg=0

测地多边形

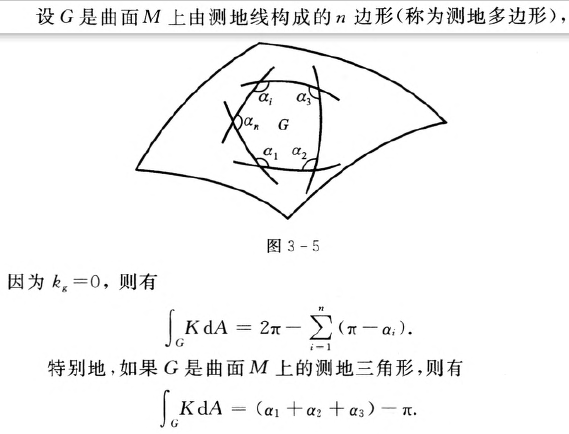
案例：

---

总结

微分几何——梅向明第四版学习笔记（一） & 向量函数和曲线论