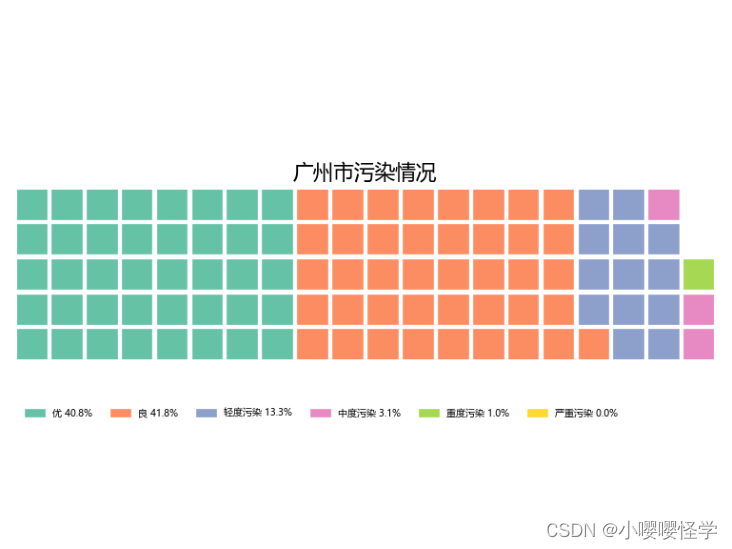
目录
1、基本概念
2、栈(Stack)
3、队列(Queue)
4、串(String)
1、基本概念
(1)线性表是零或多个数据元素的有限序列。
(2)数组长度指存储空间长度,线性表长度指数据元素个数。
(3)顺序存储结构的三个属性:数组data,数组长度MAXSIZE,线性表当前长度length;查找时间复杂度为O(1),插入删除的时间复杂度为O(n)。
插入算法思路:
(i) 如果插入位置不合理,抛出异常;
(ii) 如果线性表长度 ≥\geq 数组长度,则抛出异常或动态增加容量;
(iii) 从最后一个元素开始向前遍历到第 i 个位置,分别将它们都向后移动一个位置;
(iv) 将要插入的元素填入位置i处,表长+1即可。
删除算法思路:
(i) 如果删除位置不合理,抛出异常;
(ii) 取出删除元素;
(iii) 从删除元素位置开始遍历到最后一个元素位置,将它们都向前移动一个位置,表长-1即可。
(4)链式存储结构,查找时间复杂度为O(n),插入删除时间复杂度为O(1)。
(i) 结点(Node)包含数据域(存储数据元素信息)和指针域(存储直接后继位置)。
(ii) n个结点连接成一个链表,即线性表的链式存储结构。
(iii) 链表第一个结点的存储位置称为头指针(链表的必要元素),最后一个结点指针为空NULL。
(iv) 常在单链表的第一个结点前附设一个结点,称为头结点,其数据域可以不存储任何信息,指针域则存储指向第一个结点的指针。头结点非必需元素,若线性表为空表,则头结点指针域为空NULL。

假设p是指向线性表第 i 个元素的指针,则数据域表示为p -> data,值为数据元素;指针域表示为p -> next,值为一个指针,指向第 i+1个元素,关系如下图所示:
(5)静态链表:用数组描述的链表
(i) 数组元素都由data和cur组成,前者存放数据元素,后者相当于单链表中的指针,存放该元素的后继在数组的下标。如下将甲、乙、丙、丁、戊等数据存入静态链表:
(ii) 优点是在插入删除操作中只需要修改cur而不用移动元素,缺点是仍连续存储,表长难以确定。
(6)循环链表(Circular Linked List):终端结点的指针由空NULL改为指向头结点即形成循环。
(7)双向链表(Double Linked List):每个结点再额外设置一个指向其前驱结点的指针域即可。
双向链表的结点表示关系有p -> next -> prior相当于 p 也相当于p -> prior -> next。
(i)插入操作顺序思路:s -> prior = p; s -> next = p -> next; p ->next ->prior = s; p ->next = s;
(ii)删除操作顺序思路:p -> prior -> next = p ->next; p ->next ->prior = p -> prior; free (p);
2、栈(Stack)
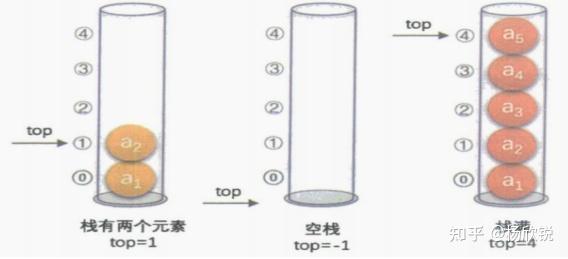
(1)栈是只在表尾即栈顶(top)端进行插入即进栈(push)和删除即出栈(pop)操作的线性表。另一端称为栈底(bottom),属于先进后出(Last In First Out)即LIFO结构。
(2)栈的顺序存储结构
定义下标为0的一端作为栈底,top变量指示栈顶元素在数组中的位置,若栈长为Stack_Size,则top必须小于Stack_Size。通常将空栈的判定条件设为top为-1,当栈存在一个元素时,top等于0。
(3)栈的链式存储结构
把栈顶top放在单链表头部,链栈为空就是 top == NULL 的时候。
顺序栈与链栈的进栈push出栈pop操作时间复杂度均为O(1),但顺序栈需要实现确定一个固定长度,方便存取;链栈则每个元素额外添加指针域,增大内存开销。
(4)栈的应用——递归——斐波那契数列
递归就是调用自己。我们把直接调用自己或者通过一系列调用语句间接地调用自己的函数称为递归函数。每个递归定义必须至少有一个条件,满足时递归不再进行,即不再引用自身而是返回值退出。以下模拟代码中 i=5 的执行过程:
(5)栈的应用——四则运算表达式求值
(i) 后缀表示法(Reverse Polish Notation):所有的符号都是在运算数字后面出现,省去括号。
正常表达式:9 + (3-1) * 3 + 10 / 2
后缀表达式:9 3 1 - 3 * + 10 2 / +
规则:从左到右遍历表达式每个数字和符号,遇到数字就进栈,遇到符号则将处于栈顶两个数字出栈,进行运算,运算结果出栈,一直到最终获得结果。
(ii) 中缀表达式转后缀表达式
标准四则运算表达式9 + (3 - 1) * 3+10 / 2 称为中缀表达式,则转后缀表达式的规则如下:
从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级不高于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,直到最终输出后缀表达式为止 。

3、队列(Queue)
(1)只允许在一端进行插入操作,而在另一端进行删除操作的线性表。允许插入的一端称为队尾(Rear),允许删除的一端称为队头(Front),属于先进先出(First In First Out)的FIFO操作。

(2)队列顺序存储结构
(i) front指针指向队头元素,rear指针指向队尾元素的下一个位置,当front == rear时队列为空。
(ii) 设一个长度为5的数组初始状态如下图所示,先让 a1a_{1} 、a2a_{2}、a3a_{3}、a4a_{4}入队,接着a1a_{1}和a2a_{2}出队,再让a5a_{5}入队,整体入队出队的流程如下图,最终rear指向队列外会形成假溢出现象。因此队列也经常采用循环结构。
(iii) 循环队列:头尾相接的顺序存储队列结构,使插入删除时间复杂度为O(1)。更新队列已满的条件是(rear + 1) % Queue_Size == front,通用队列元素个数的计算公式为(rear - front + Queue_Size) % Queue_Size。
(3)队列链式存储结构
(i) 队列链式结构实际就是只能尾进头出的单链表,队头指针front指向链队列的头结点,队尾指针rear指向终端结点。空队列时,front和rear都指向头结点。
(ii) 入队操作就是在链表尾部插入结点,出队操作就是头结点的后继结点出队,将头结点的后继改为它后面的结点,若链表除了头结点外只剩一个元素,则需将rear指向头结点。

(4)从时间上,循环队列和链队列的入队出队操作都是O(1);空间上看,循环队列需要一个固定长度,有存储元素个数和空间浪费的问题。若可以确定队列MAX长度,可用循环队列,若无法预测队列长度,则用链队列。
4、串(String)
(1)串是由零个或多个字符组成的有限序列,一般记为s = " a1a_{1}a2a_{2}a3a_{3}a4a_{4}……ana_{n}"(n ≥\geq 0),字符数目n称为串的长度。无字符无任何内容的串称为空串"",但空格串是只包含空格的串" ",有内容也有长度。
(2)串的比较通过组成串的字符之间的编码,如给定两个串:s = " a1a_{1}a2a_{2}a3a_{3}a4a_{4}……ana_{n}"(n ≥\geq 0),t = " b1b_{1}b2b_{2}b3b_{3}b4b_{4}……bmb_{m} "(m≥\geq0),当满足以下条件之一时,s < t。
(i) n < m,且 aia_{i} < bib_{i} ( i = 1,2,……,n)
(ii)存在某个 k < min(m,n),使得aia_{i} = bib_{i} ( i = 1,2,……,k-1),aka_{k} < bkb_{k}
(3)串的顺序存储结构:用一组地址连续的存储单元来存储字符序列。
(4)串的链式存储结构:容易造成空间浪费,不够灵活。
(5)KMP模式匹配算法
把子串各个位置 j 值的变化定义为一个数组next,则next的长度就是子串的长度,函数定义为:

前缀:包含首字母但不包含尾字母的所有子串;后缀:只包含尾字母但不含首字母的所有子串。
next数组值即寻找子串中“最大的相同前后缀长度的下一个”,前两个值为0、1。
Next_val数组由next数组得到,首位为0,下一位字符它的next值与 j 序号对应,若对应字符不同,则next_val值即为next值;若对应字符相同,则next_val值同为对应j序号的next_val值。

注:KMP模式匹配算法有不同标准表达方式,重在理解思想即可。这里推荐在B站搜KMP相关高播放量网课,看看代码随想录卡哥录的或是动画演示那些,有助于理解消化