注：这篇文章主要是留给自己查漏补缺的，所以从来没有使用过yalmip的读者看着会觉得跳来跳去。

基本用法

建模开始前，使用yalmip('clear')清空Yalmip的内部数据库。
下面是一个完整的建模例子，包括定义决策变量、约束、目标函数，并求解。如果求解成功，那么输出最优解；否则，使用sol.info,yalmiperror(sol.problem)分析求解出错的原因。

% It's good practice to start by clearing YALMIPs internal database 
% Every time you call sdpvar etc, an internal database grows larger
yalmip('clear')% Define variables
x = sdpvar(10,1);% Define constraints 
Constraints = [sum(x) <= 10, x(1) == 0, 0.5 <= x(2) <= 1.5];
for i = 1 : 7Constraints = [Constraints, x(i) + x(i+1) <= x(i+2) + x(i+3)];
end% Define an objective
Objective = x'*x+norm(x,1);% Set some options for YALMIP and solver
options = sdpsettings('verbose',1,'solver','quadprog','quadprog.maxiter',100);% Solve the problem
sol = optimize(Constraints,Objective,options);% Analyze error flags
if sol.problem == 0% Extract and display valuesolution = value(x)
elsedisplay('Hmm, something went wrong!');sol.infoyalmiperror(sol.problem)
end

变量定义

P=sdpvar(n,n)默认会定义出一个对称的决策变量矩阵，如果不希望它是对称的，那么要补全第三个参数P=sdpvar(n,m,'full');
约束P>=0中，如果P=sdpvar(n,n)，那么这个约束是正定矩阵的约束，如果你想要表达每个元素都是非负的，可以使用P(:)>=0；如果P=sdpvar(n,m,'full')，那么这个约束表示矩阵中每个元素都要是非负的。
yalmip不支持严格不等式约束，如果你一定要用的话，可以自定义一个tolerance，选择合适的tolerance是需要技巧的，设置太小了可能会被忽略达不到你想要的效果，设置太大了可能会切掉问题可行域中的一大块。

my_tolerance_for_strict = 1e-5;
F = [0 <= P(1,1) <= 2-my_tolerance_for_strict, P >= eye(n)*my_tolerance_for_strict];

Note though, many times strict inequalities are part of a homogenous problem, and the problem should be dehomogenized by adding a single constraint such as P>=eye(n) and replace all other constraints with non-strict. 这句话没看懂，什么是同质问题？？

关于大M

引入大M会给混合整数规划求解器带来糟糕的数值问题，并松弛后的问题变弱了，这引发过多的分支并增加求解时间。
可以考虑tight bound of the big-M reformulations来缓解松弛后的问题过弱的痛点，具体地，可以为每个决策变量增加相应的上下界约束。
大M建模的目的是，生成一个模型使得它的松弛能够尽可能地接近原约束的convex hull，也就是，原问题可行域的最好的凸近似。
在Yalmip中，可以直接使用hull生成convex hull,

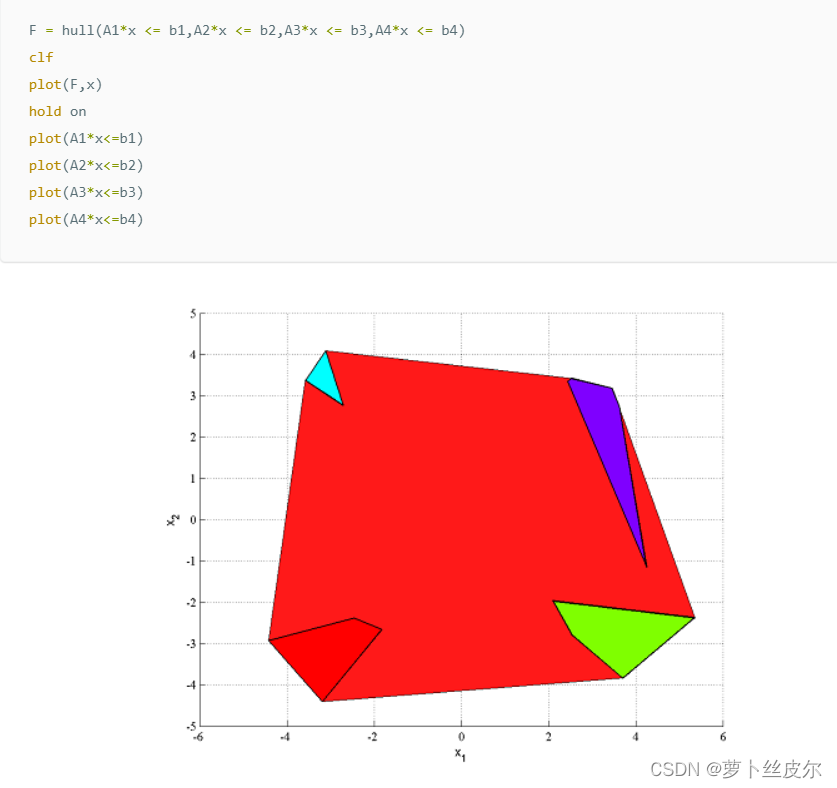
结合生成的hull, 你可以得到更强的混合整数规划模型

M1 = 50;
M2 = 50;
M3 = 50;
M4 = 50;
F = sum(d) == 1;
F = [F, A1*x - b1 <= M1*(1-d(1))];
F = [F, A2*x - b2 <= M2*(1-d(2))];
F = [F, A3*x - b3 <= M3*(1-d(3))];
F = [F, A4*x - b4 <= M4*(1-d(4))];
F = [F, hull(A1*x <= b1,A2*x <= b2,A3*x <= b3,A4*x <= b4)];

注意，这里的hull()命令会引入很多约束和变量。

Bilevel programming

https://yalmip.github.io/tutorial/bilevelprogramming/
yalmip里面有KKT函数接口；
对于双层规划问题，yalmip内部的求解器要求内层问题有二次凸性（convex quadratic）, 外层问题不一定要有凸性。
求解外层问题时，不停地重复分支定界流程，由互补松弛定理所带来的等式约束随后加入求解。