动态博弈的描述

前两章分析的博弈中，所有参与人都同时行动，这样的博弈被称为静态博弈。这一章我们开始关注动态博弈。不同于静态博弈，动态博弈中的参与人行动有先后顺序，后行动者在先行动者做出决策之后再选择自己的行动。生活中大部分博弈属于动态博弈。比如，下棋时，一方先走，另一方后走；买东西时消费者和商家的讨价还价，一方先出价，另一方再还价；谈婚论嫁，一方求婚，另一方决定是否应允。企业之间的价格战往往也是以动态方式进行，一方先降价，另一方再跟进。

由于动态博弈行动有先后顺序，在描述动态博弈时，需要把参与人行动的顺序刻画出来，所以，博弈论中常用博弈树（game tree）描述动态博弈，如下图所示：

这个博弈可以理解为市场进入博弈（设想为一个规模不大的市场，只能有一个企业可持续生存）。图中空心圆圈表示初始决策点，实心点表示之后的决策点，从决策点后引申的直线叫做路径（path），代表参与人在特定时点上的行动。参与人（企业）A首先选择“进入”或“不进入”; A选择后B再做选择。假如A首先选择进入，如果B同样选择进入，则两人得到的收益都为-1；如果B选择不进入，则A得到1, B得到0。假如A选择不进入，如果B选择进入，则A、B得到的收益分别为0和1；如果B也选择不进入，则各自得到0。习惯上，在博弈树最后的支付组合中，第一个数字表示第一个采取行动的人的收益，第二个数字表示第二个采取行动的人的收益（三人及三人以上的博弈以此类推）。

用博弈树的方法来描述动态博弈可以很直观地表明参与人的行动顺序、信息和收益。不足之处在于，博弈树无法直接表明参与人的战略，需要我们根据行动和信息等条件来确定。

作为行动计划的战略

在静态博弈里，战略和行动是一样的。但在动态博弈里，参与人的决策是在不同时点做出的，因而战略并不一定是单一的行动，而是一个完备的行动计划，要为参与人在每个时点上规定一个行动。比如在上述博弈中，A首先行动，他的决策不可能建立在B行动的基础上，所以其战略是进入或者不进入，但B不一样：B后行动，他可以根据A的选择制定自己的行动计划。这样的话，由于A有两个不同选择，B依据A的每一个选择又具有两个不同的选择，从而B总共有4个战略：

战略1：无论A进入还是不进入，B都选择进入；

战略2：如果A进入，则B不进入；如果A不进入，则B进入；

战略3：如果A进入，则B进入；如果A不进入，则B也不进入；

战略4：无论A进入还是不进入，B都选择不进入。

对于B来说，上述的4个战略相当于4个行动计划。他需要在博弈开始之前为自己确定一个行动计划。假如B宣称自己将会选择战略1，即“无论A进入还是不进入，B都选择进入”，这时A将如何选择？

如果A相信B真的选择这一战略的话，自己选择进入，就会得到-1，而如果自己不进入可以得到0，因此A的最优选择是不进入。实际上，A选择不进入和B选择战略1构成了一个纳什均衡，因为：给定A不进入，B的战略也是最优的；给定B的战略，A不进入是最优的。但问题是B的声明可信吗？

静态博弈中，参与人一旦选定战略（行动）后，就不会改变了。但是，在动态博弈中，参与人在博弈开始前选择的战略（行动计划）可能在博弈开始后进行调整，不一定按照原定的战略（行动计划）来进行。也就是说，事前最优的战略在事中或事后不一定是最优的。在本例中，B在事前声称要选择战略“不管A进入不进入，自己都选择进入”，但一旦A没有理会这一声明，选择了“进入”，此时B就会发现选择原来的战略并不是最优的，因为如果他此时改为选择“不进入”可以得到0，而坚持原定战略会得到-1。这说明B声明自己会选择战略1并不可信。

生活中，这种声明可能是“威胁性”的（threat），类似“如果你不答应做某事，我就会如何”，也可能是“许诺性”的（promise），类似“如果你答应做某事，我会如何”。其实“威胁性”声明可以变成“许诺性”声明，比如，“如果你不答应做某事，我就会如何”可以改变为“如果你答应不做某事，我会如何”。一个例子是，家长管教孩子，可以威胁性地说，“如果你不答应放弃玩游戏，我要扣除你这个月的零花钱”；也可以许诺性地说，“如果你答应放弃玩游戏，我就不扣除你这个月的零花钱”。同样，许诺性的声明也可以变成威胁性的声明。这样，从分析的角度来看，就没有必要对威胁性声明和许诺性声明加以区分了。其实质都是发出声明的一方希望以此来影响对方的行动。因此，下文我们就把这些声明统称为“威胁”。

威胁的可信性

“威胁”是现实生活中经常遇到的问题。比如，员工可能扬言，如果不给加薪就报复上司；热恋中的女子可能威胁说，如果男方与她分手，她就不再活下去；存在领土争议的国家可能宣称，如果对方不让步，就诉诸武力，等等。

当博弈的一方发出威胁，接到威胁的一方就需要判断这一威胁是否可信。如前述分析，这一威胁可信性问题的根源是动态博弈中事前最优和事后最优的不一致性。而适用于静态博弈的解概念——纳什均衡并没有考虑这种动态不一致性。因此，当我们用纳什均衡概念来求解动态博弈时，有可能会出现包含不可置信威胁（non-credible threat）的纳什均衡。

下面我们通过分析学校里的师生博弈来说明这一问题。学校设计的课程是为了给学生传授知识，考试的目的是通过评价学生的成绩督促学生认真学习。出于职业道德和声誉的考虑，老师一般会根据学生答题的情况给出公平的分数，如及格还是不及格。但无论实际考得如何，学生都希望老师给个好成绩，至少及格，因为考试成绩关系到学生的利益，包括能不能顺利毕业，以及能否找到满意的工作。现假定有一个学生平时没有好好学习，期末考试考得不好，到不了60分。他去找老师希望老师能够让他及格。因此，我们有如下的师生博弈：

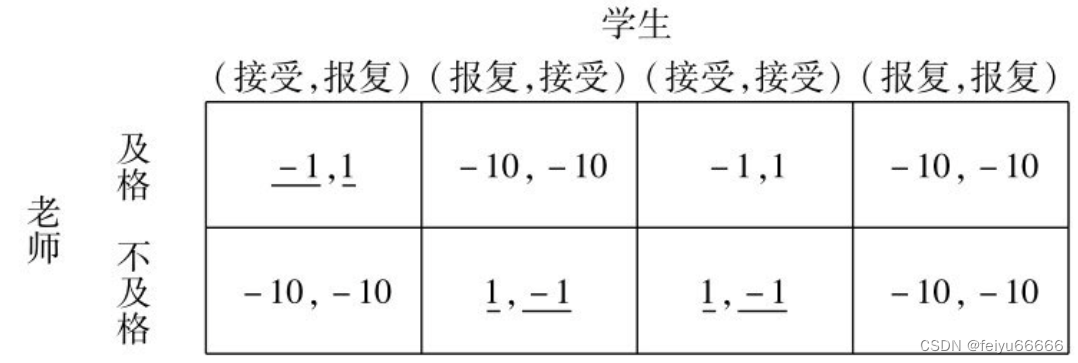
老师先行动，他的战略是判卷时给学生及格或不及格；学生后行动，他的战略是依据老师所给他的成绩来决定自己是欣然接受这一成绩还是要报复老师。所谓欣然接受是指认可老师给出的分数；所谓报复老师是指对老师采取一些人身或名誉伤害的行动。

具体来说，学生会有4个战略可选择：

战略1：如果老师给及格，则欣然接受；如果给不及格，则报复老师。

战略2：如果老师给及格，则报复老师；如果给不及格，则欣然接受。

战略3：不管老师是否给及格，都欣然接受。

战略4：不管老师是否给及格，都报复老师。

双方的收益情况是：如果老师违心给了学生及格，学生没有报复他，他的收益为-1，学生的收益为1；如果他违心给了学生及格，但学生还是报复了他，则他的收益为-10，此时学生也因为报复老师被学校处分，收益也为-10；如果老师秉公给了学生不及格，学生报复，则老师为-10，学生也为-10；如果老师秉公给了学生不及格，学生接受，则老师收益为1，学生为-1。

可以将学生上述的4种策略相应地简记为（接受，报复）、（报复，接受）、（接受，接受）、（报复，报复）。这里，（接受，报复）读为：如果老师给及格，就接受；如果老师给不及格，就报复。类似地，（报复，接受）、（接受，接受）、（报复，报复）可以做相应的解读。这样，我们就可以把上述博弈用下图所示的战略式（即标准式）来描述。

通过划线法求解这个博弈的纳什均衡，可以发现共有三个纳什均衡：

第一个纳什均衡是“老师选择及格，学生选择（接受，报复）”。均衡结果是：老师选择及格，学生不报复；双方的收益为：老师-1，学生1。意思是，学生前来找老师时声称自己将选择（接受，报复），即老师给及格就接受，不给及格就报复。老师担心自己会报复，违心地打了及格，故收益为-1。而学生呢，本来自己不会及格，现在及格了，故收益为1。这一纳什均衡隐含着老师屈从学生的威胁。但学生如果真的报复老师的话，又会遭受学校更为严厉的处罚，使得他的收益成为-10。因此，如果学生理性的话，应不会选择报复。进一步，如果老师知道学生是理性的，就不应该相信其威胁。所以，这一纳什均衡尽管满足互为最优，但却包含了一个不可置信（non-creditable）的威胁。

第二个纳什均衡是“老师选择不及格，学生选择（报复，接受）”。均衡结果是：老师选择不及格，学生不报复；双方的收益为：老师1，学生-1。直观含义是，学生声称老师给及格就报复，不给及格就接受，而老师则该给不及格就给了不及格。老师因为公正评分，得到的收益为1，而学生选择接受，得到不及格的结果，收益为-1。但这一纳什均衡中，学生的战略（报复，接受）要求在老师给及格的情况下选择报复，但报复又会让其得到-10的收益。所以，这其实也是一个不可置信的威胁。

第三个纳什均衡是“老师选择不及格，学生选择（接受，接受）”。均衡结果是：老师选择不及格，学生接受；双方的收益为：老师1，学生-1。意思是，学生的态度很端正，不管老师给不给及格，自己都能接受，老师则实事求是，该给不及格就给了不及格。老师因为公正评分，得到的收益为1，而学生选择接受，得到不及格的结果，收益为-1。这个纳什均衡比较合理，没有包含不可置信的威胁在里面。

上述三个纳什均衡中的前两个都包含了不可置信的威胁。为什么这两个纳什均衡会包含不可置信的威胁或者说不合理的战略呢？这是因为动态博弈中会出现动态不一致性：事先最优战略和事后最优战略会不一样。学生事先宣布其要采取的战略（比如“及格则接受，不及格就报复”等），从事后看可能并不是最优，因为如果老师真的判了不及格（或及格），学生的最优选择是接受。因而这样的威胁是不可信的。这就意味着，我们不能简单地把纳什均衡应用到动态博弈中。动态博弈需要能够反映动态一致性、排除不可置信威胁的均衡概念。因此，我们需要对原来的纳什均衡概念进行改进。